10. Плотность вероятности непрерывной случайной величины, ее определение, свойства и график.

Определение. Плотностью вероятности (плотностью распределения или просто плотностью) непрерывной случайной величины Х называется производная ее функции распределения

Про случайную величину Х говорят, что она имеет распределение (распределена) с плотностью на определенном участке оси абсцисс. Плотность вероятности, как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения она существует толькодля непрерывных случайных величин. Плотность вероятности иногда называют дифференциальной функцией или дифференциальным законом распределения. График плотности вероятности называетсякривой распределения.

Свойства плотности вероятности непрерывной случайной величины.

1. Плотность вероятности - неотрицательная функция, т.е. .

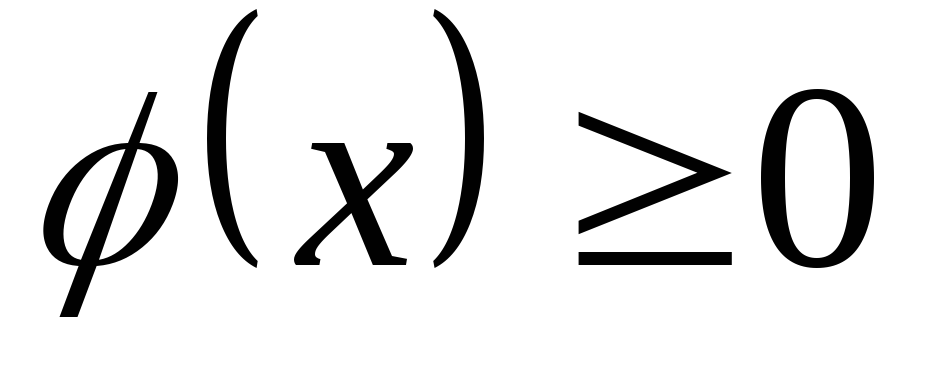☺ как производная монотонно неубывающей функции F(х). ☻

2. Вероятность попадания непрерывной случайной величины в интервал [а,b] равна определенному интегралу от ее плотности вероятности в пределах от а до b, т.е. .

☺Согласно свойству 4 функции распределения . Так как F(x) - первообразная для плотности вероятности(т.к., то по формуле Ньютона-Лейбница приращение первообразной на отрезке [а,b] – определенный интеграл . ☻

Геометрически полученная вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок [а,b] (рис. 3.8).

3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

.

Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения и лежащей левее точки х (рис. 3.9).

4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице: .

Геометрически свойства 1 и 4 плотности вероятности означают, что ее график - кривая распределения - лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

10. Случайная величина, распределенная по биномиальному закону, ее математическое ожидание и дисперсия. Закон распреде­ления Пуассона.

Определение. Дискретная случайная величина Х имеет биномиальный закон распределения с параметрами npq, если она принимает значения 0, 1, 2,..., m,... ,n с вероятностями

,

где 0<р<l, q=1-p.

Как видим, вероятности Р(Х=m) находятся по формуле Бернулли, следовательно, биномиальный закон распределения представляет собой закон распределения числа Х=m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.

Ряд распределения биномиального закона имеет вид:

Очевидно, что определение биномиального закона корректно, т.к. основное свойство ряда распределения выполнено, ибоесть не что иное, как сумма всех членов разложения бинома Ньютона:

Математическое ожидание случайной величины Х, распределенной по биноминальному закону,

а ее дисперсия

Определение. Дискретная случайная величина Х имеет закон распределения Пуассона с параметром λ > 0, если она принимает значения 0, 1, 2,..., m, ... (бесконечное, но счетное множество значений) с вероятностями ,

Ряд распределения закона Пуассона имеет вид:

Очевидно, что определение закона Пуассона корректно, так как основное свойство ряда распределения выполнено, ибо сумма ряда.

На рис. 4.1 показан многоугольник (полигон) распределения случайной величины, распределенной по закону Пуассона Р(Х=m)=Р_m(λ) с параметрами λ = 0,5, λ = 1, λ = 2, λ = 3,5.

Теорема. Математическое oжидaниe и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е.

и