10. Функция распределения нормально распределенной случай­ной величины и ее выражение через функцию Лапласа.

Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, и вероятности ее попадания на некоторый промежуток связана с тем, что интеграл является «неберущимся». В элементарных функциях. Поэтому их выражают через функцию:

.

- функцию (интеграл вероятностей) Лапласа, для которой составлены таблицы. Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [-х; х] (рис. 4.8).

Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:

.

□ По формуле функция распределения:.

Сделаем замену переменной, полагая ,,при,, поэтому

.

Первый интеграл

.

(В силу четности подынтегральной функции и того, что интеграл Эйлера-Пуассона равен ).

Второй интеграл с учетом составляет .

Итак, . ■

10. Формулы для определения вероятности: а) попадания нормально распределенной случайной величины в заданный интер­вал; б) ее отклонения от математического ожидания. Правило «трехсигм».

Свойства случайной величины, распределенной по нормальному закону:

1. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал , равна ,

Где ,.

□ Учитывая, что вероятность есть приращение функции распределения на отрезкеи учитывая формулуполучим:

. ■

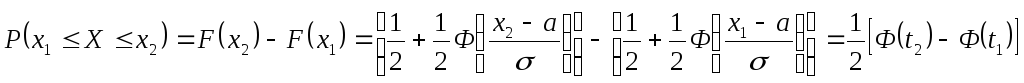2. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину (по абсолютной величине), равна , где .

□ . Учитывая свойство 1, а также свойство нечетности функции Лапласа, получим

. ■

«правило трех сигм»:

Если случайная величина Х имеет нормальный закон распределения с параметрами а и , т.е. N(a;), то практически достоверно, что ее значения заключены в интервале ().

Нарушение «правила трех сигм», т.е. отклонение нормально распределенной случайной величины Х больше, чем на (по абсолютной величине), является событием практически невозможным, так как его вероятность весьма мала:

.

10. Понятие двумерной (/7-мерной) случайной величины. При­меры. Таблица ее распределения. Одномерные распределения ее составляющих. Условные распределения и их нахождение по таб­лице распределения.

Очень часто результат испытания характеризуется не одной СВ, а некоторой системой случайных величин , которую называют такжемногомерной (n-мерной) случайной величиной или случайным вектором Х = ().Приведем примеры многомерных случайных величин.

1. Успеваемость выпускника вуза характеризуется системой n случайных величин - оценками по различным дисциплинам, проставленными в приложении к диплому.

2. Погода в данном месте в определенное время суток может быть охарактеризована системой случайных величин: - температура;- влажность;- давление;- скорость ветра и т.п.

Любая СВ (i = 1,2,...,n) есть функция элементарных событий ω, входящих в пространство элементарных событий Ω (). Поэтому имногомерная случайная величина есть функция элементарных событий ω:

т.е. каждому элементарному событию ω ставится в соответствие несколько действительных чисел , которые приняли случайные величиныв результате испытания. В этом случае вектор х = () называетсяреализацией случайного вектора Х = ().

Случайные величины , входящие в систему, могут быть какдискретными (см. выше пример 1), так и непрерывными (пример 2).

Наиболее полным описанием многомерной СВ являетсязакон ее распределения. При конечном множестве возможных значений многомерной СВ такой закон может быть задан в форме таблицы (матрицы), содержащей всевозможные сочетания значений каждой из одномерных случайных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X,Y), то ее двумерное распределение можно представить в виде таблицы (матрицы) распределения (табл. 5.1), в каждой клетке (i,j) которой располагаются вероятности произведения событий .

Так как события (i = 1,2,...,n; j = 1,2,...,m), состоящие в том, что СВ Х примет значение , а СВY - значение , несовместны и единственно возможны, т.е. образуют полную группу, то сумма их вероятностей равна единице, т.е.:

Распределение одномерной случайной величины Х можно получить, вычислив вероятность события (i = 1,2,...,n) как сумму вероятностей несовместных событий:

.

Аналогично .

Т.о., чтобы по таблице распределения (табл. 5.1) найти вероятность того, что одномерная случайная величина примет определенное значение, надо просуммировать вероятности из соответствующей этому значению строки (столбца) данной таблицы.

Если зафиксировать значение одного из аргументов, например, положить , то полученное распределение случайной СВ Х называетсяусловным распределением Х при условии . Вероятности этого распределения будутусловными вероятностями события , найденными в предположении, что событиепроизошло. Из определения условной вероятности:

.

Аналогично условное распределение СВ У при условии задается с помощью условных вероятностей:.