10. Математическое ожидание и дисперсия числа и частости на­ступлений события в п повторных независимых испытаниях (с выводом).

Математическое ожидание частости события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью р, равно р, т.е. а ее дисперсия .

□ Частость события есть, т.е., где Х - случайная величина, распределенная по биномиальному закону. Поэтому

. ■

10. Определение нормального закона распределения. Теоретико-вероятностный смысл его параметров. Нормальная кривая и зависимость ее положения и формы от параметров.

Определение. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и , если ее плотность вероятности имеет вид:

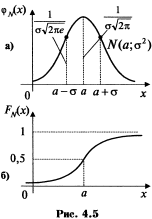
Термин «нормальный» не совсем удачный. Многие признаки подчиняются нормальному закону, например, рост человека, дальность полета снаряда и т.п. Но если какой-либо признак подчиняется другому, отличному от нормального, закону распределения, то это вовсе не говорит о «ненормальности» явления, связанного с этим признаком.

Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рис. 4.5 а, б приведены нормальная кривая с параметрами а и, т.е., и график функции распределения случайной величины Х, имеющей нормальный закон.

Обратим внимание на то, что нормальная кривая симметрична относительно прямой х=а, имеет максимум в точке х=а, равный , т.е., и две точки перегибас ординатой.

Можно заметить, что в выражении плотности нормального закона параметры обозначены буквами а и , которыми мы обозначаем математическое ожидание М(Х) и дисперсиюD(Х). Такое совпадение неслучайно. Рассмотрим теорему, устанавливающую теоретико-вероятностный смысл параметров нормального закона.

Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона, т.е. , а ее дисперсия - параметру , т.е. .

□ Математическое ожидание случайной величины Х:

. Произведем замену переменной, положив . Тогдаи, пределы интегрирования не меняются и, следовательно,.

(первый интеграл равен нулю как интеграл от нечетной функции по симметричному относительно начала координат промежутку, а второй интеграл - интеграл Эйлера­Пуассона).

Дисперсия случайной величины Х:

.

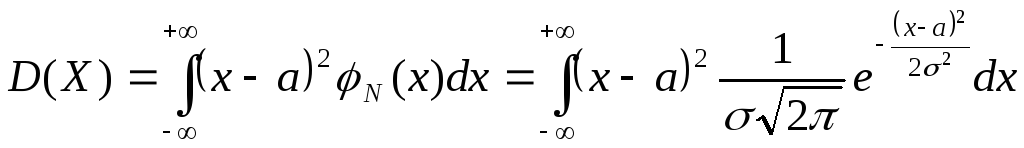Сделаем ту же замену переменной , как и при вычислении предыдущего интеграла. Тогда

.

Применяя метод интегрирования по частям, получим:

.■

Выясним, как будет меняться нормальная кривая при изменении параметров а и (или). Если, и меняется параметр а (), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 4.6).

Если a=const и меняется параметр(или), то меняется ордината максимума кривой. При увеличенииордината максимума кривой уменьшается, но так как площадь под любой кривой распределения должна оставаться равной единице, то кривая становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении а, напротив, нормальная кривая вытягивается вверх, одновременно сжимаясь с боков. На рис. 4.7 показаны нормальные кривые с параметрами, где. Т.о., параметр а (он же математическое ожидание) характеризуетположение Центра, а параметр (он же дисперсия) -форму нормальной кривой.

Нормальный закон распределения случайной величины с параметрами а=0, =1, т.е. N(0;l), называетсястандартным или нормированным, а соответствующая нормальная кривая - стандартной или нормированной.