Если проецирующая плоскость параллельна другой плоскости проекций, то она называется плоскостью уровня (рис. 59).

		а								б
							Рис. 58
		α1			x1 2
								2
х
1 2

а	б	в
	Рис. 59

На рис. 59 представлены плоскости: α π1 и ║π2 – горизонтальная

(рис. 59, а); β π2 и ║π1 – фронтальная (рис. 59, б); τ π1, π2

и ║ π3 – профильная (рис. 59, в).

3.5. Аксонометрия

Ещё одним частным случаем метода двух изображений является аксонометрия.

Аксонометрия – это наглядное изображение, полученное путём параллельно-ортогонального проецирования.

3.5.1. Модель точки в аксонометрии

Пусть плоскости π1 и π2 расположены под произвольным углом друг к другу, который может оказаться прямым. Проецирование на плоскость π1

64

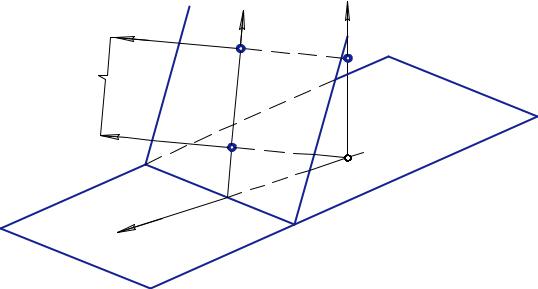
параллельное (в частном случае может быть ортогональным), на π2 – обязательно ортогональное (рис. 60). Так как оба центра S1 и S2 бесконечно удалены, то и точки U1 и U2 также окажутся бесконечно удалёнными.

	1	U1	S2
		A1
			A
S1
		A2	A2
U2		x1 2
	2

Рис. 60

Возьмём произвольную точку А пространства и спроецируем её на обе плоскости проекций. Полученная пара проекций А1 и А2 представляет собой пространственную модель точки А в аксонометрии.

Для перехода к плоской модели изображение, полученное на π2, спроецируем из S1 на π1. Получим пару проекций А1 и А2′, расположенных на одной линии связи в плоскости π1, которую затем совмещаем с плоскостью чертежа. Они и являются аксонометрической моделью точки А про-

странства. А1 называется первичной проекцией, или аксонометрией, А2′ –

вторичной проекцией точки А. В дальнейшем в целях упрощения первичную проекцию будем обозначать просто буквой А, а её вторичную проекцию – А .

3.5.2. Виды аксонометрии

Для того чтобы по аксонометрическому изображению можно было определить не только форму, но и размеры объекта, на модели необходимо иметь изображение координатных осей x, y, z с натуральными единицами измерения.

В пространстве оси x, y, z взаимно перпендикулярны, а единичные отрезки ОЕ равны между собой. ОЕ – натуральная единица измерения. Если эту координатную систему спроецировать на плоскость проекций, то получим проекции x′, y′, z′ координатных осей и проекции О′Ех, О′Еy, О′Еz натуральных единиц измерения (рис. 61).

65

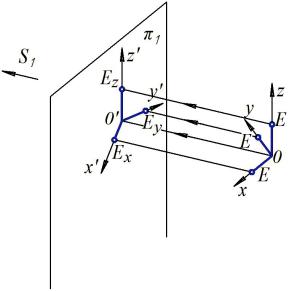
Проекции x′, y′, z′ будем называть аксонометрическими осями, а отрезки О′Ех, О′Еy, О′Еz – аксонометрическими единицами. Углы между x′, y′, z′ могут быть любыми. Единичные отрезки также проецируются с искажением. При этом может оказаться, что длины отрезков О′Ех, О′Еy, О′Еz либо все разные, либо только два одинаковые, либо все три одинаковые.

Рис. 61

Отношениедлинаксонометрическойединицыкнатуральнойназывается показателемиликоэффициентомискаженияпосоответствующейоси:

p	O Ex	;	q	O E y	;	r	O Ez	.
	OE			OE			OE

Если p = q = r, то по всем осям имеем одну и ту же единицу измерения. Такая аксонометрия называется изометрией (от греческого «изо» – один, единый). Если p = r q, то имеем два разных измерения. Аксонометрия называется диметрией (от греческого «ди» – два). Если p r q, то имеем триметрию.

Аксонометрия, полученная ортогональным проецированием, называется прямоугольной. Аксонометрия, полученная косоугольным проецированием, называется косоугольной.

Таким образом, существует шесть видов аксонометрии: прямоугольная изометрия, прямоугольная диметрия, прямоугольная триметрия, косоугольная изометрия, косоугольная диметрия, косоугольная триметрия.

3.5.3. Стандартные аксонометрии

Для выполнения чертежей ГОСТ 2.317–69 рекомендует пять видов аксонометрических проекций: две прямоугольные и три косоугольные. Остановимся на стандартных прямоугольных аксонометриях.

66

Прямоугольная изометрия. Все углы между осями по 1200. Ось z′

расположена вертикально (рис. 62, а). В прямоугольной аксонометрии коэффициенты искажения связаны следующей зависимостью: p2 + q2 + r2 = 2, а так как в изометрии все коэффициенты равны, то можно записать 3p2 = 2.

Отсюда				. Таким образом, натуральный коэффициент ис-
		2⁄3
кажения по				0,82
	всем осям 0,82. Это значит, что при построении аксонометрии

все откладываемые размеры необходимо умножить на 0,82. Но на практике это неудобно. Поэтому натуральный коэффициент округляют до ближайшего целого числа. Полученный коэффициент называется приведённым.

а

б

Рис. 62

Итак, прямоугольная изометрия строится с приведёнными коэффициентами p = q = r = 1. Аксонометрическое изображение при этом увеличится в 1/0,82 ≈ 1,22 раза по сравнению с ортогональным чертежом.

Прямоугольная диметрия. Ось z′ расположена вертикально, ось х′ – подуглом7°10′кгоризонтали, y′– подуглом41°25′кгоризонтали (рис. 62, б). Натуральный коэффициент искажения по осям х′ и z′ – 0,94, по оси y′ – 0,47. На практике пользуются приведенными коэффициентами p = r = 1, q = 0,5, что дает увеличение аксонометрии в 1/0,94 ≈ 1,06 раза.

3.5.4. Практические рекомендации по построению аксонометрии

Построение осей

Прямоугольная изометрия. Берем две взаимно перпендикулярные прямые. Из точки пересечения проводим дугу произвольного радиуса. Из точки пересечения дуги с вертикальной прямой тем же радиусом делаем засечки на дуге. Оси х′ и y′ пройдут через О′ и полученные засечки

(рис. 63, а).

67

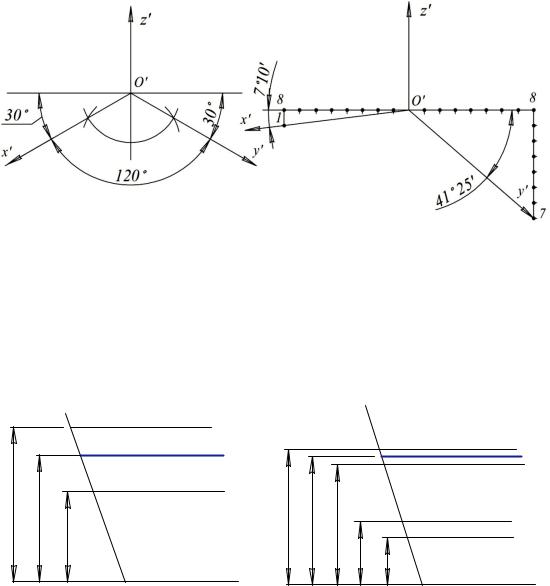
Прямоугольная диметрия. Проводим две взаимно перпендикулярные прямые. По горизонтали вправо и влево от О′ откладываем по 8 равных отрезков произвольной длины. Из концов последних отрезков опускаем вниз вертикали и откладываем слева 1, а справа 7 таких же отрезков. Оси х′ и y′ пройдут через концы вертикальных отрезков и О′ (рис. 63, б).

а

б

Рис. 63

Треугольник пропорциональности

Для перехода от одного масштаба к другому рекомендуется использовать треугольник пропорциональности. Построим два таких треугольника для аксонометрии окружности: один в изометрии, другой в диметрии.

			1,22
			1:1
48,8			0,71
	40(1)	28,4	42,4	40(1)	38	20	15
		A					A
		а					б
			Рис. 64

1,06 1:1

0,95

0,5 0,35

Прямоугольная изометрия (рис. 64, а). На произвольном расстоянии друг от друга (например 40 мм), принимаемом за единичное, проводим две параллельные прямые. Верхнюю прямую принимаем за шкалу натурального масштаба. От нижней прямой откладываем расстояния, пропорциональ-

ные коэффициентам 1,22 и 0,71 (40×1,22 = 48,8; 40×0,71 = 28,4), и через

68

Рис. 65

полученные отметки проводим прямые, параллельные первым двум. Затем проводим прямую, пересекающую все шкалы под произвольным углом. В точке пересечения ее с каждой прямой будет начало отсчета соответствующей шкалы. Верхняя шкала будет с коэффициентом 1,22, нижняя – с коэффициентом 0,71.

Размеры, взятые с чертежа, откладываем на натуральной шкале и из точки А проецируем их на нужную шкалу.

Прямоугольная диметрия (рис. 64, б). Построения выполняются так же, как в изометрии, с той лишь разницей, что коэффициенты берем 1,06; 0,35; 0,5; 0,95.

Почему взяты именно такие коэффициенты станет ясно, когда рассмотрим аксонометрию окружности.

Аксонометрия окружности

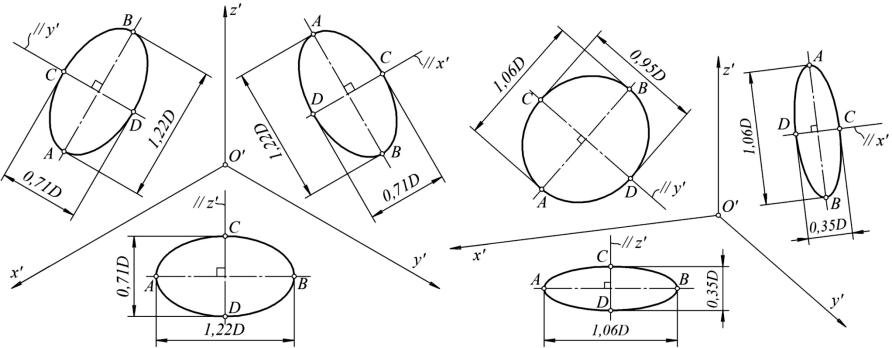
Окружность в аксонометрии изображается в виде эллипса (рис. 65), который характеризуется двумя сопряженными диаметрами ЕF и КL

идвумя осями: АВ (большая ось) и СD (малая ось). Сопряженные диаметры являются изображением взаимно перпендикулярных диаметров окружности

инаправлены вдоль аксонометрических осей.

	Оси эллипса взаимно перпендикулярны	K	C	F
	(АВ CD) и определяют ориентацию эллипса
	в каждой аксонометрической плоскости.
	В прямоугольной аксонометрии малая	A		B
	ось эллипса всегда параллельна той аксоно-
	метрической оси, которая не лежит в плоско-	E		L
	сти эллипса. Так, если эллипс расположен в		D
	плоскости х′О′у′, то малая ось параллельна z′,

в плоскости х′О′z′ – параллельна у ′, в плоскости у′О′z′ – параллельна х′.

На рис. 66, а показана ориентация осей эллипса и их размеры для прямоугольной изометрии. На рис. 66, б – для прямоугольной диметрии.

Приемы построения эллипса

Эллипс может быть построен как лекальная и как циркульная кривая. Лекальная кривая строится по точкам, которые затем плавно соеди-

няются от руки или при помощи лекала (способ 1).

Циркульная кривая строится при помощи циркуля как кривая, состоящая из сопрягающихся дуг окружностей (способы 2, 3).

Рассмотрим построение эллипса в аксонометрической плоскости х′О′y′. Аналогичными будут построения в других плоскостях. Только необходимо учитывать ориентацию осей эллипса (как показано на рис. 66).

69

70

а

б

Рис. 66

Возьмём окружность произвольного радиуса и построим её прямоугольную изометрию и диметрию разными способами, заготовив предварительно треугольники пропорциональности (рис. 67).

Рис. 67

Способ 1. Лекальная кривая. Строим аксонометрию по восьми точкам, которыми будут являтьсяконцы осей и сопряжённых диаметров.

В прямоугольной изометрии (рис. 68, а) приведённые коэффициенты искажения по всем осям равны 1. Поэтому на осях х′ и у′ от центра О откладываем радиус R окружности, на оси z′ – малую полуось эллипса 0,71R, на прямой, перпендикулярной z′, – большую его полуось 1,22R.

а

б

Рис. 68

Для определения размеров большой и малой полуосей эллипса откладываем на натуральной шкале (1:1) треугольника пропорциональности для изометрии радиус окружности R, и из точки А проецируем его на ос-

71

тальные шкалы. На верхней шкале получаем размер 1,22R, на нижней –

0,71R.

В прямоугольной диметрии (рис. 68, б) по осям х′ и z′ коэффициент искажения равен 1, по оси у′–0,5. Поэтому на оси х′ откладываем радиус R. Остальные размеры определяем при помощи треугольника пропорциональности для диметрии. На натуральной шкале (1:1) откладываем радиус R и через точку А и конец этого отрезка проводим проецирующий луч. На шкале 0,5 берём размер 0,5R для оси у′, на шкале 0,35 – размер 0,35R малой полуоси эллипса, который откладываем на z′. Размер 1,06R большой полуоси берём со шкалы 1,06 и откладываем его на прямой, перпендикулярной z′.

Полученные восемь точек в обоих случаях предпочтительнее соединить при помощи лекала.

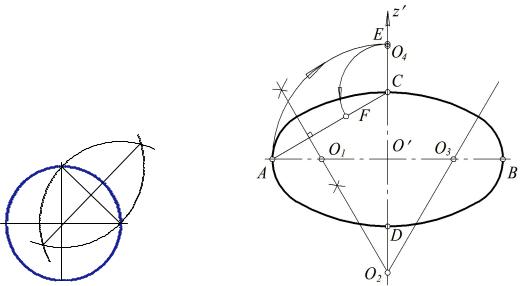
Примечание. Размеры осей эллипса для прямоугольной изометрии можно определить и графически (рис. 69). Для этого из концов С и D взаимно перпендикулярных диаметров окружности проводим дуги радиусом CD до взаимного пересечения в точках А и В. Соединив точки А и В, получим большую ось эллипса, равную 1,22D, а отрезок СD будет его малой осью, равной 0,71D.

Способ 2. Коробовая кривая. Коробовая кривая является циркульной кривой, состоящей из четырёх дуг окружностей (рис. 70). Ею можно заменить эллипс. Строится она по его осям.

C	B
	D
A
Рис. 69	Рис. 70

На рис. 70 коробовая кривая построена в прямоугольной изометрии. Малая ось CD направлена вдоль оси z′, большая АВ ей перпендикулярна. Построение выполняем в определённой последовательности.

● Соединяем концы большой и малой полуосей (отрезок АС).

72

●Находим разность большой и малой полуосей (отрезок СЕ). Для этого из центра О радиусом О А проводим дугу до пересечения с прямой, проходящей через CD, в точке Е.

●Откладываем СЕ от точки С на АС. Получаем точку F.

●Строим срединный перпендикуляр к отрезку AF и отмечаем точки пересечения его с прямыми линиями, проходящими через оси эллипса. О1

иО2 – центры двух дуг окружностей.

●Замеряем расстояния от О1 и О2 до О′ и откладываем их по другую

сторону от центра эллипса (О О1 О О3, О О2 О О4). Получаем ещё два

центра О3 и О4.

● Соединяем попарно центры и проводим дуги из центра О1 радиусом О1А, из О2 – радиусом О2С, из О3 – радиусом О3В и из О4 – радиусом О4D до пересечения с линиями центров.

На рис. 71 построена прямоугольная диметрия окружности в плоскости х′О′z′ в виде коробовой кривой. Малая ось CD направлена вдоль оси у′ и равна 0,95D. Большая ось АВ у′ и равна 1,06D. Последовательность построения та же, что была рассмотрена выше для изометрии.

E	C	B
	F
	O	O
	4
	O	3
	1	O
		2
		D
	A	y'

Рис. 71

Этот метод является универсальным и может применяться не только для построения аксонометрии окружности, но и любого эллипса или овала, если известны размеры его большой и малой оси, чем широко пользуются при конструировании технических деталей.

Способ 3. Овал. Построим прямоугольную изометрию окружности в плоскости х′О′у′, заменяя эллипс овалом (рис. 72)

Задаём аксонометрические оси х′, у′, z′ и направление большой оси эллипса (перпендикулярно z′). Из центра эллипса проводим окружность радиусом, равным радиусу той окружности, аксонометрию которой строим. На пересечении этой окружности с направлением малой оси эллипса (осью z′) получаем два центра дуг – О1 и О2. Проводим прямые через О1

73

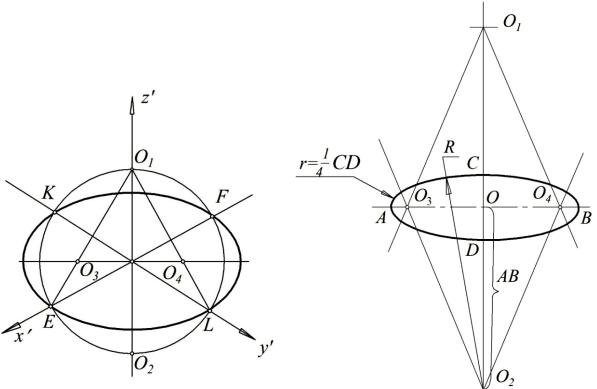
и точки Е, L (или через О2 и точки K, F) пересечения окружности с осями х′, у′. На пересечении их с направлением большой оси получаем ещё два центра – О3 и О4. Затем последовательно проводим из центра О1 дугу ЕL радиусом О1Е, из центра О4 – дугу LF радиусом О4 L, из О2 – дугу FK радиусом О2F, из О3 – дугу KE радиусом О3K.

Построенный овал неточно повторяет форму эллипса. У них имеются небольшие расхождения в размерах. Таким приёмом можно построить овал только в прямоугольной изометрии.

На рис. 73 показано построение овала, заменяющего эллипс в прямоугольной диметрии. Овал строится по осям и пригоден только для эллипсов, у которых малая ось в три раза меньше большой оси (в плоскостях х′О′у′ и z′О′у′). Рассмотрим построение овала в плоскости х′О′у′.

Рис. 72

Рис. 73

Проводим две взаимно перпендикулярные прямые. Одну вертикально (параллельно z′), другую горизонтально. Точка пересечения прямых будет центром О эллипса. Отрезки АВ и СD – соответственно большая и малая ось эллипса. По обе стороны от центра О на прямой, проходящей через малую ось СD, откладываем отрезки, равные длине большой оси АВ эллипса. Получаем центры О1 и О2 двух дуг окружностей. Центры О3 и О4 двух других дуг окружностей удалены от концов А и В большой оси эллипса на расстояние 1/4CD. Соединяем попарно центры и между линиями центров проводим дуги: из О1 радиусом О1D, из О4 радиусом О4В, из О2

74

радиусом О2С, из О3 радиусом О3А. Как следует из построений, радиусы сопрягающихся дуг равны R = AB + 1/2CD, r = 1/4CD.

Коробовая кривая и овал представляют собой кривые, приближенные к эллипсу. Существуют и другие способы построения эллипса.

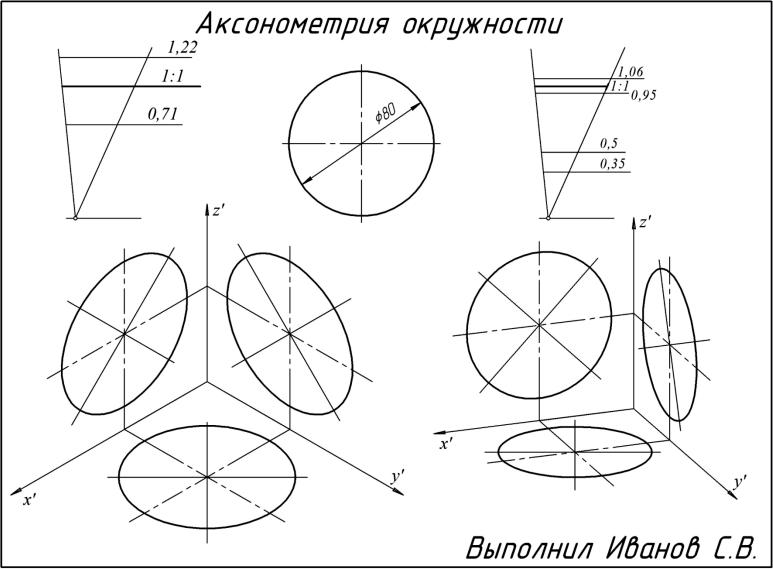
3.5.5. Задание № 8. Аксонометрия окружности

Цель: изучение приёмов построения аксонометрии окружности во всех трёх аксонометрических плоскостях.

Взять окружность диаметром 80 мм и построить ее изображение в прямоугольной изометрии и прямоугольной диметрии, используя все три рассмотренных выше способа построения эллипса (в разных плоскостях разными способами). Для диметрии коробовую кривую построить в плоскости х′О′z′. Все построения необходимо показать полностью. В левом и правом верхнем углу построить треугольники пропорциональности. Точки можно не подписывать.

Задание выполнить на листе формата А3, компоновка которого показана на рис. 74.

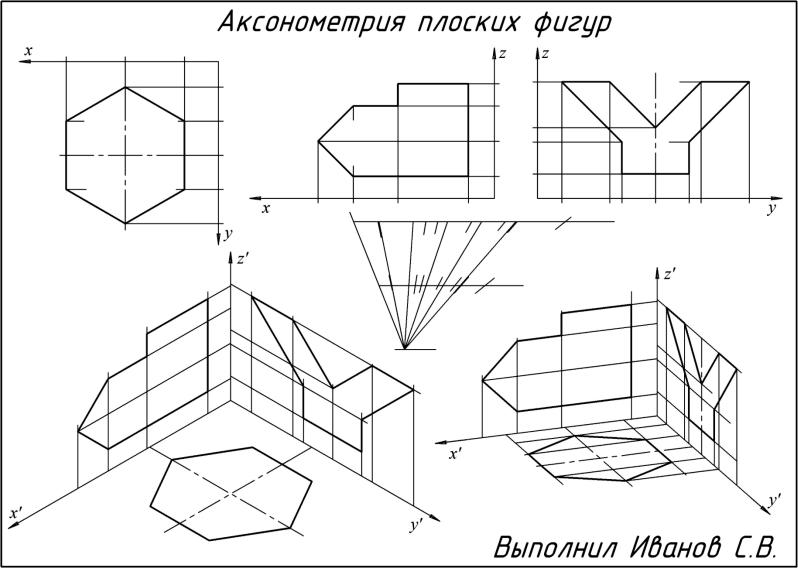
3.5.6. Аксонометрия плоской фигуры

Построение аксонометрии любого геометрического тела начинается с построения его основания. Поэтому рассмотрим, какими приемами можно строить аксонометрию плоской фигуры.

Параллельность прямых в аксонометрии сохраняется. Эта особенность активно используется при построении аксонометрических проекций. Прежде чем приступить к построению аксонометрии плоской фигуры, так же как и любого геометрического тела, необходимо на ортогональном чертеже задать оси координат. Построение аксонометрии выполняется в соответствии с привязкой фигуры к координатной системе. При этом следует иметь в виду, что

●ось х всегда должна быть направлена горизонтально, ось у – верти-

кально;

●все измерения выполняются только по осям или параллельно им;

●все прямые линии, параллельные между собой или параллельные координатным осям на ортогональном чертеже, остаются параллельными

ив аксонометрии (рис. 75).

При построении аксонометрии симметричной фигуры координатные оси можно совместить с её осями симметрии. На рис. 75 задана горизонтальная проекция A2B2C2D2E2F2 шестиугольника ABCDEF. Ось х совмещена с горизонтальной осью симметрии шестиугольника, ось y – c его вертикальной осью. Рядом построена прямоугольная изометрия этого шестиугольника.

75

76

Рис. 74

Вершины А и D можно построить сразу. Они лежат на оси х. Замеряем расстояние ОА2 ОD2 и откладываем его на х по обе стороны от начала координат. Остальные четыре вершины на осях не лежат. Они расположены на прямых, параллельных оси х. Замеряем расстояние по оси у от точки О до В2С2, E2F2 и откладываем его на у от начала координат. Через полученные отметки проводим прямые, параллельные оси х , и откладываем на них по обе стороны от у половину длины сторон В2С2, E2F2. Соединив последовательно все вершины, получаем прямоугольную изометрию ABCDEF заданного шестиугольника. Из полученного чертежа видно, что в аксонометрии параллельность противоположных сторон сохранилась: AB║DE, BC║EF, CD║AF, а равенство всех сторон – нет.

Если многоугольник имеет неправильную форму, то его аксонометрия строится по координатам вершин (рис. 76).

Рис. 75

Для этого надо «привязать» фигуру к координатным осям. Координатные оси задаются на любом расстоянии от проекции (рис. 76, а). Определяются координаты вершин (Ах, Вх, Сх и Аy, Вy, Сy) в выбранной системе, затем переносятся на аксонометрические оси с учетом коэффициента искажения. Для переноса удобно использовать полоску бумаги. Её прикладывают к координатной оси на ортогональном чертеже и отмечают на ней начало координат и координаты всех точек. Затем, если по соответствующей аксонометрической оси коэффициент искажения равен 1, то эту полоску прикладывают к аксонометрической оси, переносят на неё эти отметки, совместив начало координат обеих систем (рис. 76, б). Если же по оси коэффициент искажения равен 0,5, то полоску с отметками прикладывают к натуральной шкале треугольника пропорциональности (рис. 76, в), совместив отметку начала координат с началом отсчёта на шкале. Проецируют отрезки на шкалу 0,5, «снимают» их на другую полоску бумаги

77

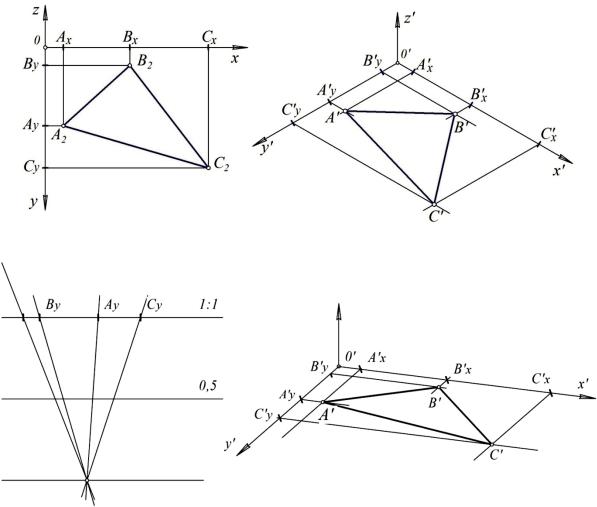
и переносят на соответствующую аксонометрическую ось (рис. 76, г). На рис. 76, б построена прямоугольная изометрия, а на рис. 76, г – прямоугольная диметрия треугольника АВС. Вершины треугольника в аксонометрии получаются при пересечении прямых, параллельных х′ и y′, проведенных через координатные отметки.

а

б

в

г

Рис. 76

Примечание. Аксонометрическая система координат бывает правой

илевой в зависимости от того, в какую сторону направлена ось х′. Направление оси на ортогональном чертеже и в аксонометрии должно быть одно

ито же. На рис. 76 задана правая система координат.

3.5.7. Задание № 9. Аксонометрия плоских фигур

Цель: научиться строить прямоугольную аксонометрию плоской фигуры во всех трёх аксонометрических плоскостях.

78

Построить прямоугольные аксонометрии трёх заданных фигур в аксонометрических плоскостях.

Один из приведённых ниже вариантов задания выполнить на листе формата А3. Лист расположить горизонтально. Рамкой ограничить рабочее поле чертежа. В верхней части листа вычертить в масштабе 1:1 три заданные фигуры выбранного варианта. Размеры не проставлять. Ниже задать аксонометрические оси для прямоугольной изометрии и прямоугольной диметрии, а также треугольник пропорциональности с коэффициентами 1 и 0,5 для уменьшения размеров вдоль оси у прямоугольной диметрии. Вычертить аксонометрию первой фигуры в плоскости ХОY, второй – в плоскости ХОZ, третьей – в плоскости YОZ, предварительно задав соответствующие координатные оси на чертежах. Образец представлен на рис. 77.

Варианты задания

79

80

81

Рис. 77