Рис. 47

3.МОДЕЛИ ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ ПРОСТРАНСТВА

Впроекционном черчении рассматриваются способы отображения объектов трехмерного пространства на плоскость чертежа или, что то же самое, создание их плоской модели. Любой пространственный объект состоит из геометрических образов. Геометрический образ – это точка, прямая, плоскость, поверхность. Чтобы работать с моделями объектов пространства, необходимо сначала хорошо разобраться в плоских моделях геометрических образов.

Геометрическая модель должна быть взаимно однозначной. Это значит, что конкретному геометрическому образу пространства на плоскости соответствует одна единственная модель и, наоборот, конкретной модели на плоскости проекций в пространстве соответствует тот же самый геометрический образ. Такая простейшая модель может быть получена пу-

тём линейного проецирования.

Каждый геометрический образ представляет собой совокупность точек. Поэтому, получив модель точки, мы сможем сконструировать модели любого другого геометрического образа. Рассмотрим подробнее как получить модель точки.

3.1.Операция линейного проецирования

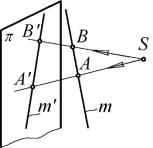
Выберем в пространстве плоскость π и точку S, не принадлежащую π.

Точку S назовем центром проецирования, а плоскость π – плоскостью проекций Центр S и плоскость π составляют аппарат проецирования.

Возьмём произвольную точку А пространства. Через точки S и А проведём лучSA) и отметим его пересечение с плоскостью проекций: SA ∩ π = А (рис. 47).

Луч SA) называется проецирующим лучом. Точка пересечения проецирующего луча с плоскостью проекций называется проекцией точки пространства: А′ – проекция точки А.

Поскольку проецирующими элементами являются прямые линии, то рассмотренное проецирование называется линейным. При таком проецировании проекцией точки будет точка, проекцией прямой линии – прямая линия. На рис. 47 m′ – проекция прямой m.

56

3.2. Виды проецирования

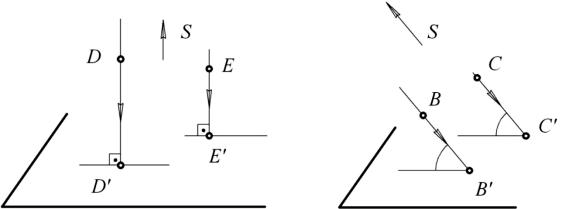
Когда все проецирующие лучи сходятся в одной точке, то говорят, что центр проецирования находится на конечном расстоянии. Такое проецирование называется центральным. Оно показано на рис. 47.

Если проецирующие лучи проходят параллельно друг другу, то говорят, что центр проецирования бесконечно удален. Бесконечно удалённая точка задаётся направлением в виде стрелочки. Все лучи должны быть параллельны этому направлению. Такое проецирование называется параллельным (рис. 48). Оно в свою очередь подразделяется на ортогональное и косоугольное.

Если проецирующие лучи перпендикулярны плоскости проекций, то проецирование называется ортогональным (рис. 48, а).

а

б

Рис. 48

Если проецирующие лучи проходят под острым углом к плоскости проекций, то проецирование называется косоугольным (рис. 48, б).

3.3. Метод двух изображений

Можно ли считать проекцию К однозначной моделью произвольной точки К пространства? Порассуждаем.

Проецирующий луч, проведённый через точку К пространства, пересечёт плоскость проекций в единственной точке К (рис. 49, а). В таком случае говорят, что точке К пространства соответствует единственная проекция К плоскости π. Записывается это следующим образом: К К .

Теперь рассмотрим соответствие в обратную сторону. Возьмём в плоскости π проекцию К (рис. 49, б) и проведём через неё проецирующий луч. Любая точка этого луча может иметь своей проекцией К , т. е. К К,

57

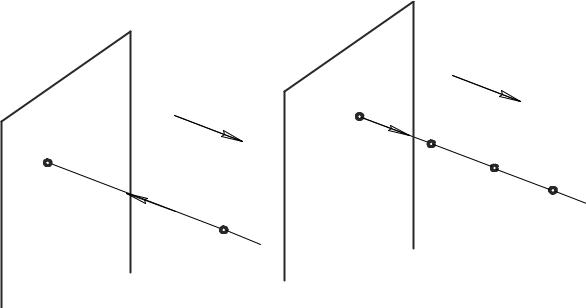
К1, К2, … . Таким образом, в обратную сторону однозначности нет. Следовательно, не возникает взаимно однозначного соответствия между точкой пространства и одной её проекцией на плоскость π. Значит, одну проекцию точки пространства нельзя считать её однозначной моделью.

			S
		K'
S
K'		K	K 1
			K 2
	K

а	б
	Рис. 49

Удвоим аппарат проецирования. Возьмем в пространстве две плоскости – π1 и π2, расположенные под произвольным углом друг к другу, и два центра – S1 и S2. Пусть проецирование на обе плоскости будет центральным (рис. 50).

Линию пересечения плоскостей проекций назовем осью проекций. Обозначим ее х12 = π1∩π2. Линию S1S2, соединяющую центры проецирования, назовем линией центров. Отметим точки пересечения ее с π1 и π2:

S1S2∩π1 = U1, S1S2∩π2 = U2.

Возьмем произвольную точку А пространства и спроецируем ее из S1

иS2 на π1 и π2. Проекцию точки будем обозначать той же буквой, что и сама точка, указывая внизу индекс той плоскости, на которую она спроеци-

рована. Получим пару проекций А1 и А2. Докажем, что они определяют однозначную модель точки А.

Центры S1, S2 и проецируемая точка А определяют некоторую плоскость α. Она пересекает плоскости проекций π1 и π2 по прямым U1X = α ∩ π1

иU2X = α ∩π2, где Х = α ∩ х12. Так как проецирующий луч S1A проходит через две точки, лежащие в плоскости α, то он весь лежит в этой плоскости. Поэтому точка пересечения его с плоскостью π1 обязательно попадет на

прямую U1X, т. е. А1 U1X. По тем же самым соображениям проекция А2 должна попасть на U2X, т. е. А2 U2X. Точки А1 и А2 будут единственными,

58

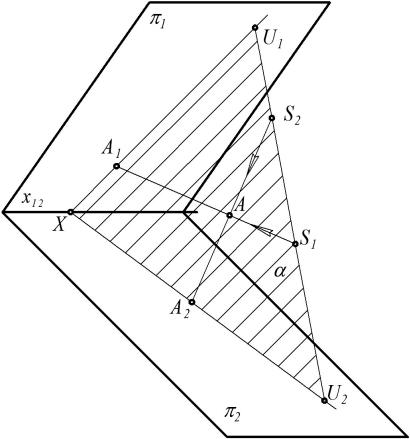
поскольку прямая и плоскость пересекаются в одной точке. Таким образом, можно сказать, что произвольной точке А пространства поставлена в соответствие единственная пара проекций А1, А2: А (А1, А2).

Справедливо и обратное утверждение. Представим, что имеем цен-

тры S1, S2, плоскости π1, π2 с точками U1, U2 и две проекции А1 U1X,

A2 U2X.

Рис. 50

Соединим А1 с S1 и А2 с S2. Эти прямые лежат в одной плоскости α, определенной треугольником U1XU2. Следовательно, они, пересекаясь, дают единственную точку А. Таким образом, (А1,А2) А. На основании доказанного можно утверждать, что пара (А1, А2), полученная рассмотренным методом двух изображений, даёт однозначную модель точки А пространства.

Проекции А1 и А2 одной и той же точки А пространства будем в дальнейшем называть соответственными точками, а лучи U1X и U2X,

на которых они лежат – соответственными лучами.

Изменяя взаимное расположение плоскостей проекций π1, π2 и центров проецирования S1, S2, будем получать различные частные варианты метода двух изображений. Остановимся на двух из них.

59