
- •2. Понятие и виды коррел. И регресс. Задачи коррел. И регресс. Ан-за
- •3. Парн. Лин. Регресс.(плр)
- •5.Коэф-т корреляции
- •6.Предпос. М-да наим. Квадратов. Т. Г-м
- •7.Анализ точности опред. Оценок коэф-ов регрессии.
- •1. Понятие экон-ки. Осн. Задачи экон-ки.
- •8) Проверка гипотез относит. Коэф-тов лин. Ур-я регрес
- •9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
- •13. Расчет коэф-в множ. Регр-ии.
- •24/Обратная модель.
- •14. Дисперсии и станд. Ошибки коэф-в.
- •19. Проверка равенства двух коэффициентов детерминации.
- •20. Проверка гипотезы о совпадении уравнений регрессии для двух выборок
- •21. Статистика Дарбина-Уртсона
- •22.Логарифмические (лог-линейные) модели.
- •33. Метод лин.Комбинаций част.Критериев.
- •34. Метод ведущего критерия.
- •36. Метод равных и наим-их относит. Отклонени
- •37. Метод минимакса
- •38. Предмет и основные понятия теории игр
- •42. Решение матричных игр в смешанных стратегиях. Теорема о необходимом и достаточном условии смешанных стратегий
- •43.Теорема о преобразованиях эл-ов платежной матрицы
- •16. Пров стат значимости коэф ур-ния множ лин регрессии
- •44. Теорема о сведении плат-й матрицы к матрице с полож числами.
- •45. Сведение матричной игры к задаче линейного программирования
- •46. Игры с природой. Понятие риска сиатистика. Матрица рисков.
- •47. Критерии Байеса и Лапласа выбора наилучшей стратегии статистика
- •48. Критерии Вальда, Сэвиджа и Гурвица выбора наилучшей стратегии статистика.
- •49. Модели анализа основных финансовых операций.
- •50. Дисконтирование денежных потоков. Текущая стоимость проекта.
- •51. Чистая текущая стоимость инвестиционного проекта
- •52. Внутренняя норма прибыли проекта
- •Вопрос 53. Индекс прибыльности и период окупаемости проекта.
- •Вопрос 54. Влияние инфляции на денежные потоки проекта.
- •58. Осн. Понятия и опр. Спу
- •57.Анализ чувств-ти ден. Потоков проекта
- •17, 18. Проверка общ кач-ва ур множ рег-сии и статзначимостикоэф детерминации.
- •59. Правила построения сет. Графиков
- •60. Расч. Врем. Парам. Событ.
- •63. Оптимизация проекта по времени, если задан срок выполнения проекта
- •62. Линейный график комплекса работ (график Ганта). Диаграмма потребления ресурсов
- •61. Расч времен парам раб.
- •64. Оптимизац проекта по времени за счет вложен выделен сумм.Ср.
- •65. Оптимизация проекта по стоимости при нефиксированной величине критического пути.
- •66. Оптимизация проекта по стоимости при фиксированной величине критического пути
- •67. Оптимизация проекта по ресурсам
- •70. Основные соотношения, отражающие сущность моб.
- •71. Мат. Модель моб. Эк. Сущность коэф-тов прямых затрат (кпз).
- •72Испол.Моб в исслед.Взаимосв. Отрасл.Структур
- •73. Использование модели моб в прогноз.Цен
- •68.Принципиальная схема моб в снс.
- •69. Экономическое содержание квадрантов моб.
9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
Рассм-им
t-статистику:
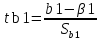
Чтоб
построить 100(1-
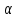 )доверит.интервал
по треб-му уровню знач-ти
)доверит.интервал
по треб-му уровню знач-ти и числу степени свободы,опред-ся критич.
знач-е:
и числу степени свободы,опред-ся критич.
знач-е:
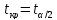 ,n-2,
кот. удовл-ет след. усл-ю:
,n-2,
кот. удовл-ет след. усл-ю:
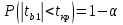
Подставим и получим.

 =
1-
=
1-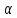
Выраж-ие в скобках и опред-ет доверит. интервал
10.
Доверит. интервалы для завис.переменной.
Одной из задач экон.модел-ния явл-ся
прогноз-ние завис.перем-ной при
опред.знач-ях независ.перем-ной. Пусть
построено ур-ние регр-ссии ŷi=b0+b1xi,
i=1,n.
Необх-мо на основе дан.ур-ния предсказать
усл.мат.ожидание M(Y/xp),
перем-ной Y при X=xp.
Знач-ния ŷр=b0+b1xр
явл-ся оценкой мат.ожидания M(Y/xp)
Возникает вопрос: как сильно может
откл-ся модельное знач-е ŷр
от
соотв-щего условного мат.ожидания
M(Y/xp)
Покажем,что случ.величина Ŷр
имеет норм.распред-ние. Для этого
исполь-ем формулы для ci
и di:
Ŷр=
ŷi=b0+b1xр=∑diyi+∑ciyixp=∑(di+cixp)yi.
След-но,случ.величина Ŷр
явл-ся лин.комб-цией норм.случ.величин
и сама имеет норм.распред-ние. Найдем
мат.ож-ние и дисп-сию дан.случ.величины:
M(Ŷ)=M(b0+b1xp)=M(b0)+M(b1)xp=β0+β1xp,
D(Ŷр)=D(b0+b1xp)=
D(b0)+xp2D(b1)+2xpcov(b0,b1),
cov(b0,b1)=M[(b0-M(b0))(b1-M(b1))]=M[(b0-β0)(b1-β1)]=M[(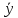 -b1
-b1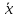 -(
-( -
β1
-
β1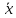 ))(b1-β1)]=M[-
))(b1-β1)]=M[-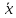 (b1-β1)(
b1-β1)]=
-
(b1-β1)(
b1-β1)]=
-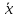 D(b1)
D(Ŷр)=
D(b0)+xp2D(b1)-2
D(b1)
D(Ŷр)=
D(b0)+xp2D(b1)-2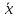 xpD(b1)=
xpD(b1)= +xp2
+xp2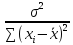 -
2
-
2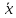 xp
xp σ2
σ2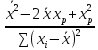 =
σ2(
=
σ2(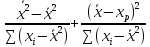 )=
σ2(
)=
σ2(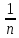 +
+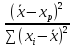 ).
Т.к. σ2
по
выборке не можно опред-ть, вместо нее
подставим ее несмещен.оценку S2=
).
Т.к. σ2
по
выборке не можно опред-ть, вместо нее
подставим ее несмещен.оценку S2=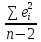 ,
тогда получим выбор.исправл.дисп-сиюслуч.величины
Ŷр:
D(Ŷр)=
S2(Ŷр)=
S2(
,
тогда получим выбор.исправл.дисп-сиюслуч.величины
Ŷр:
D(Ŷр)=
S2(Ŷр)=
S2( +
+ ).
В дальнейшем будем исполь-ть случ.величину
t=
).
В дальнейшем будем исполь-ть случ.величину
t=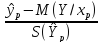 ,
кот-е имеет распредел-е Стьюдента с
числом степеней своб-ы ν=n-2. Опред-ем
критич.точку tkp=
,
кот-е имеет распредел-е Стьюдента с
числом степеней своб-ы ν=n-2. Опред-ем
критич.точку tkp=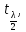 n-2
, кот. удовлетв-ет след.условию Р(
n-2
, кот. удовлетв-ет след.условию Р( <tkp)=1-𝛌.Подставим
знач-е вместо t: P(-
<tkp)=1-𝛌.Подставим
знач-е вместо t: P(-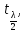 n-2<
n-2<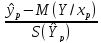 <
<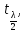 n-2)=
1-𝛌,
P(b0+b1xр-
n-2)=
1-𝛌,
P(b0+b1xр-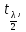 n-2
S(Ŷр)<
n-2
S(Ŷр)<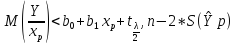 )=1-𝛌.
Выражение в скобках и опред-ет
доверит.интервал для условн. M(Y/xp).
)=1-𝛌.
Выражение в скобках и опред-ет
доверит.интервал для условн. M(Y/xp).
11.
Проверка общ.кач-ва ур-ния регр-сии.
Мера
общ.кач-ва ур-ния регр-сии,т.е.соотв-вия
ур-ния стат.данным явл-ся кофф-т
детерминации R2,кот.опред-ся
по след.форм.: R2=1-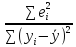 . реальн.значения завис.перем-ой отлич-ся
от модельн.знач-ний на величину еi:
yi=ŷi+ei,
i=
. реальн.значения завис.перем-ой отлич-ся
от модельн.знач-ний на величину еi:
yi=ŷi+ei,
i= .
Последнее можно переписать:yi-
.
Последнее можно переписать:yi- =(ŷi-
=(ŷi- )+(yi-
ŷi),где
yi-
)+(yi-
ŷi),где
yi-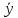 -откл-ние
i-й наблюд.точки от ср.знач-я, ŷi-
-откл-ние
i-й наблюд.точки от ср.знач-я, ŷi-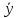 -откл-ние i-й точки на линии регр-сии от
ср.знач.,yi-
ŷi-откл-ние
i-й наблюд.точки от модельн.знач. Разделим
обе части посл.выраж-я на лев.часть:
-откл-ние i-й точки на линии регр-сии от
ср.знач.,yi-
ŷi-откл-ние
i-й наблюд.точки от модельн.знач. Разделим
обе части посл.выраж-я на лев.часть:
1=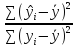 +
+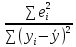 ,
,
получим
тогда исходн.форм-у. Коэф-т детерм-ции
R2
опред-ет
долю разброса завис.переменной, объяснимую
ур-нием регр-сии. Коэф-т детерм-ции: 0≤
R2≤1.
Чем ближе R2
к 1,тем лучше кач-во построен.регр-сии.
Судить о кач-ве ур-ния регр-сии можно и
по ср.ошибке аппроксимации,кот.опред-ся:Ā= ∑
∑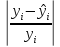 *100%,если
Ā≤10%,
то построен.ур-ние регр-сии качеств-но.
*100%,если
Ā≤10%,
то построен.ур-ние регр-сии качеств-но.
13. Расчет коэф-в множ. Регр-ии.
Данные набл-ий и соотв. коэф-ты в матрич. форме:
Y=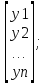 X=
X= B=
B=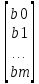 ;
e=
;
e=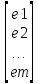
Ф-ию
Q=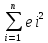 в матрич. форме можно предст-ть как
произв. вектор-строки
в матрич. форме можно предст-ть как
произв. вектор-строки на вектор-столбец е. Вектор-столб. Е
можно запис. в виде: е=У-ХВ. Тогда исход.
ф-июQ
запиш. в виде: Q=
на вектор-столбец е. Вектор-столб. Е
можно запис. в виде: е=У-ХВ. Тогда исход.
ф-июQ
запиш. в виде: Q=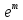 *е=
*е=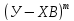 *(У-ХВ)=
*(У-ХВ)=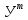 *У-
*У-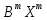 У-
У-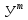 ХВ+
ХВ+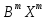 ХВ=
ХВ=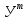 *У-2
*У-2 У+
У+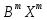 ХВ.
Мат-ки док-но, что вектор-столб част-х
произв-х ф-ииQ
по оцен. парам-м имеет вид:
ХВ.
Мат-ки док-но, что вектор-столб част-х
произв-х ф-ииQ
по оцен. парам-м имеет вид:
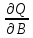 =
-2
=
-2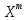 У+2
У+2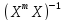 B.
Приравняв
B.
Приравняв
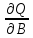 =
0 получим ф-лу для вычис-я множ. лин-ой
регр-ии:
=
0 получим ф-лу для вычис-я множ. лин-ой
регр-ии:
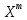 У=
У=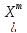 Х)В
=>
Х)В
=>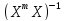 *
*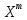 У.
У.
