
- •2. Понятие и виды коррел. И регресс. Задачи коррел. И регресс. Ан-за
- •3. Парн. Лин. Регресс.(плр)
- •5.Коэф-т корреляции
- •6.Предпос. М-да наим. Квадратов. Т. Г-м
- •7.Анализ точности опред. Оценок коэф-ов регрессии.
- •1. Понятие экон-ки. Осн. Задачи экон-ки.
- •8) Проверка гипотез относит. Коэф-тов лин. Ур-я регрес
- •9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
- •13. Расчет коэф-в множ. Регр-ии.
- •24/Обратная модель.
- •14. Дисперсии и станд. Ошибки коэф-в.
- •19. Проверка равенства двух коэффициентов детерминации.
- •20. Проверка гипотезы о совпадении уравнений регрессии для двух выборок
- •21. Статистика Дарбина-Уртсона
- •22.Логарифмические (лог-линейные) модели.
- •33. Метод лин.Комбинаций част.Критериев.
- •34. Метод ведущего критерия.
- •36. Метод равных и наим-их относит. Отклонени
- •37. Метод минимакса
- •38. Предмет и основные понятия теории игр
- •42. Решение матричных игр в смешанных стратегиях. Теорема о необходимом и достаточном условии смешанных стратегий
- •43.Теорема о преобразованиях эл-ов платежной матрицы
- •16. Пров стат значимости коэф ур-ния множ лин регрессии
- •44. Теорема о сведении плат-й матрицы к матрице с полож числами.
- •45. Сведение матричной игры к задаче линейного программирования
- •46. Игры с природой. Понятие риска сиатистика. Матрица рисков.
- •47. Критерии Байеса и Лапласа выбора наилучшей стратегии статистика
- •48. Критерии Вальда, Сэвиджа и Гурвица выбора наилучшей стратегии статистика.
- •49. Модели анализа основных финансовых операций.
- •50. Дисконтирование денежных потоков. Текущая стоимость проекта.
- •51. Чистая текущая стоимость инвестиционного проекта
- •52. Внутренняя норма прибыли проекта
- •Вопрос 53. Индекс прибыльности и период окупаемости проекта.
- •Вопрос 54. Влияние инфляции на денежные потоки проекта.
- •58. Осн. Понятия и опр. Спу
- •57.Анализ чувств-ти ден. Потоков проекта
- •17, 18. Проверка общ кач-ва ур множ рег-сии и статзначимостикоэф детерминации.
- •59. Правила построения сет. Графиков
- •60. Расч. Врем. Парам. Событ.
- •63. Оптимизация проекта по времени, если задан срок выполнения проекта
- •62. Линейный график комплекса работ (график Ганта). Диаграмма потребления ресурсов
- •61. Расч времен парам раб.
- •64. Оптимизац проекта по времени за счет вложен выделен сумм.Ср.
- •65. Оптимизация проекта по стоимости при нефиксированной величине критического пути.
- •66. Оптимизация проекта по стоимости при фиксированной величине критического пути
- •67. Оптимизация проекта по ресурсам
- •70. Основные соотношения, отражающие сущность моб.
- •71. Мат. Модель моб. Эк. Сущность коэф-тов прямых затрат (кпз).
- •72Испол.Моб в исслед.Взаимосв. Отрасл.Структур
- •73. Использование модели моб в прогноз.Цен
- •68.Принципиальная схема моб в снс.
- •69. Экономическое содержание квадрантов моб.
24/Обратная модель.
Обратной моделью(гипербола) называется модель вида: У= β0+ β1 1/Х + ε. Она сводится к линейной модели заменой 1/Х=Х*.
Данная модель применяется в тех случаях, когда неограниченное увеличение объясняющей переменной Х асимптотически приближает зависимую переменную У к к некоторому пределу β0.
12.
Множ.лин.регр-сия.Опред-е парам-в ур-ния
регр-сии.
На люб.экон.показатель чаще всего
оказыв.влияние не 1, а неск.факторов.В
этом случ.вместо парной рассм-ся
множеств.регр-ссия:М(Y/x1,x2…,xm)=f(x1,x2,…,xm).
Ур-ние множ.регр-сии в общ.виде: Y=f(β,X)+ε,
где β=( β0,
β1,…,
βm)-вектор
теоретич.коэф-тов,кот.нужно определить.
X=(X1,X2,…,Xm)-вектор
независ.переменных. Теоретич.лин.ур-ние
множ.регр-сии имеет вид:Y=
β0+β1X1+β2X2+…+βmXm+ε
или в кажд.конкр. случае: yi=
β0+
β1xi1+β2xi2+…+
βmxim+εi,
i=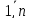 .
Число степеней свободы для множ.лин.регр-сии:
ѵ=n-m-1. Если n>m+1, то возник-ет необх-сть
оценив-ния теорет.коэф-тов регр-сии.
Будем исполь-ть метод наим.квадр-в.Должны
выполняться предпосылки Гаусса-Маркова
и еще 2 предпос-ки:а) отсутствие
мультиколлинеарности,т.е. между
независ.перемен-ми должна отсутсв-ть
сильная лин.завис-сть b)случ.отклонения
εi,
i=
.
Число степеней свободы для множ.лин.регр-сии:
ѵ=n-m-1. Если n>m+1, то возник-ет необх-сть
оценив-ния теорет.коэф-тов регр-сии.
Будем исполь-ть метод наим.квадр-в.Должны
выполняться предпосылки Гаусса-Маркова
и еще 2 предпос-ки:а) отсутствие
мультиколлинеарности,т.е. между
независ.перемен-ми должна отсутсв-ть
сильная лин.завис-сть b)случ.отклонения
εi,
i=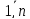 должны иметь норм.распред-ние εi
~
N(0,6).
Истинные значения коэф-тов по выборке
опред-ть невозможно, поэтому строится
импирич.ур-ние регр-сии: Ŷ= b0+b1X1+b2X2+…+bmXm.
Для каждого наблюдения мы получим:
yi=ŷi+ei,
i=
должны иметь норм.распред-ние εi
~
N(0,6).
Истинные значения коэф-тов по выборке
опред-ть невозможно, поэтому строится
импирич.ур-ние регр-сии: Ŷ= b0+b1X1+b2X2+…+bmXm.
Для каждого наблюдения мы получим:
yi=ŷi+ei,
i=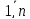 .
Для нахождения оценок b0,b1,…,bm
исполь-ся
ф-ция Q(b0,b1,…,bm)=
.
Для нахождения оценок b0,b1,…,bm
исполь-ся
ф-ция Q(b0,b1,…,bm)=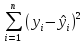 =
= →min.
Дан.ф-ция-квадратичная. Необх.условие
сущ-ния минимума-рав-во нулю всех ее
частн.производных
→min.
Дан.ф-ция-квадратичная. Необх.условие
сущ-ния минимума-рав-во нулю всех ее
частн.производных
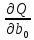 =-2
=-2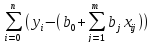 =0,
i=
=0,
i=
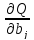 =-2
=-2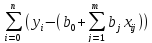 xij=0,
j=
xij=0,
j=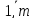 .
.
14. Дисперсии и станд. Ошибки коэф-в.
3 предпосылки для расчёта:
1)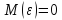
2)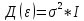
3)
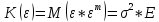 ,
где
,
где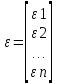 ,
,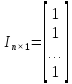 ,
,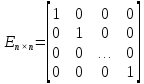 ,
,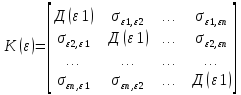
Подставим
в
 *
*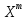 У
теор. знач-я завис-й перем-й:
У
теор. знач-я завис-й перем-й:
У=Х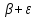 .
В=
.
В= *
*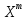 (Х
(Х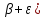 =
=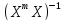 *
*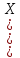 Х)
Х)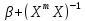 *
*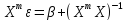 *
*
Из
послед. ф-лы => В-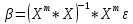 .
Строим дисперс.-ковариац-ю матрицу
вектора оц-к парам-в. К(В)=М
.
Строим дисперс.-ковариац-ю матрицу
вектора оц-к парам-в. К(В)=М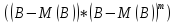 =
=
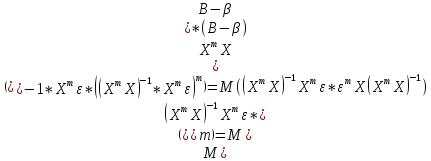 Т.к.
все независ. перем-ые
Т.к.
все независ. перем-ые
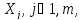 не
явл. случ. велич-ми, то получ.:
не
явл. случ. велич-ми, то получ.:
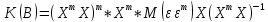 =
= =
= .
Получ., что
.
Получ., что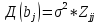 ,j=0,m,
где
,j=0,m,
где
 – диогональн. элем-т матрицы
– диогональн. элем-т матрицы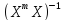 .
Знач-ие дисп-ии
.
Знач-ие дисп-ии замен-ся несмещ-ой оц-кой
замен-ся несмещ-ой оц-кой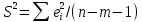 .
Поэтому по выборке опр-ем выборочн.
дисперсии эмпирич. коэф. регрессии.
.
Поэтому по выборке опр-ем выборочн.
дисперсии эмпирич. коэф. регрессии.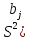 )=
)= ,j=0,m.
Как и в парной регр-ии
,j=0,m.
Как и в парной регр-ии
 – стандарт. ош-ка регр-ии;
– стандарт. ош-ка регр-ии;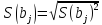 -станд. ош-ка коэф-та регр-ии.
-станд. ош-ка коэф-та регр-ии.
15.
Интерваль. оц-ки коэф-в теор-го ур-ния
множ-й регр-сии. Для
опр-ия интервал. оц-к строится t-статистика:
t
=
 .
Она имеет число степ-ей свободы
.
Она имеет число степ-ей свободы
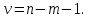 По выбран. ур-ню значимости
По выбран. ур-ню значимости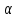 опр-ем
опр-ем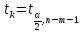 ,
которое удовлетвор. соотнош-ю:
,
которое удовлетвор. соотнош-ю: )
= 1-
)
= 1- .
Преобраз-м и получим доверит. интервалы
вида:
.
Преобраз-м и получим доверит. интервалы
вида: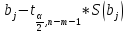 <
<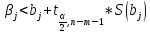 ,
где
,
где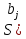 )=
)=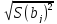 =
=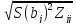 =
= . Аналог-но в парн регр-ии можно построить
в матрич. форме оц-ку для ср. знач. завис-ей
перемен-й, когда Х=
. Аналог-но в парн регр-ии можно построить
в матрич. форме оц-ку для ср. знач. завис-ей
перемен-й, когда Х=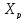 .
.
19. Проверка равенства двух коэффициентов детерминации.
Пусть построенное по n наблюд-ям урав-е регр-ии имеет вид:
 и
коэф-т детерминации для этой модели
равен
и
коэф-т детерминации для этой модели
равен
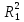 .
Исключим из рассм-нияk
объясняющих перем-ых. По первонач. n
наблюд-ям для оставшихся факторов
построим другое урав-е регр-и:
.
Исключим из рассм-нияk
объясняющих перем-ых. По первонач. n
наблюд-ям для оставшихся факторов
построим другое урав-е регр-и:
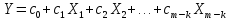 , для
кот. коэф-т детерм-ции равен
, для
кот. коэф-т детерм-ции равен
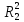 .
Очевидно, что
.
Очевидно, что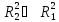 .
.
Возн-ет
вопрос: существенно ли ухуд-сь кач-во
описания поведения зависимой перем-ой
Y.
На него можно ответить, проверяя гипотезу
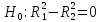 и используя статистику:
и используя статистику:

В
случае справед-ти
 F имеет распред-ие Фишера с числами
степеней свободы
F имеет распред-ие Фишера с числами
степеней свободы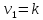 ,
,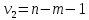 .
.
По
таблицам критич. точек распред-ия Фишера
находят
 .
.
Если
F>Fкp.,
то нулевая гипотеза о равенстве коэфф-ов
детерминации должна быть отклонена,
т.е. одновременное исключение из рассм-ия
k
объясняющих перем-ых некорректно, так
как
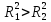 (общее кач-во первонач. урав-я регр-ии
лучше кач-ва урав-я регр-ии с отброш.
перем-ыми.
(общее кач-во первонач. урав-я регр-ии
лучше кач-ва урав-я регр-ии с отброш.
перем-ыми.
Если же F<Fкр., то одноврем-ое отбрас-е k объясняющих перем-ых не привело к существ. ухудш-ю общего кач-ва урав-я регр-ии, и оно вполне допустимо.
Аналогичные рассуждения могут быть использованы и по поводу обоснованности включения новых k объясняющих переменных. В этом случае рассчитывается F-статистика

Если она > Fкp. то включение новых перем-ых оправдано, и наоборот.
