33. Метод лин.Комбинаций част.Критериев.

При решении задач данным методом вводится вектор весовых коэф.,кот.характ.важность соотвюкритерия.

α=(α1,α2,…αк), αк>0

Тогда целевая ф-ция будет представлять собой един.частных критериев,умноженных на весовые коэф.При этом критерии обязат.должны быть нормированы.

maxF(x)=Сумм αк*fк(x)

λi(x){<= >=}bi,i=1,m

xj>=0,j=1,n

34. Метод ведущего критерия.

Этот метод явл.частным случаем метода последовательных уступок.В этом методе все критерии,кроме маиого важного,переводятся в разряд ограничений.

Умножив все критерии минимизации ф-ции на -1 и обозначив через ß=(ß2,ß3..ßк)нижние границы соотв.критериев,тогда модель задачи будет меть вид:

maxF(x)=f1(x)

fk(x)>=ßk, k=2,k

λi(x){<=,=,>=}bi,i=1,m

xj>=0,j=1,n

Будем решать задачу по к критериям:

max f₁ =

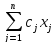
max f₂ =

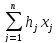
min f_k =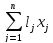 , k=3,k

( ≤ , = , ≥ ) b_i , i=1,m

x_j ≥ 0, j=1,n

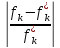
Запишем условия равенства относит.отклонений критериев от их экстримальн.значений.

==…=

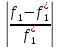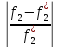Рассмотрим 4 первых критерия. По условию задачи f₁ и f₂ максимизир-ся, а f₃, f₄-минимизир-ся. Проанализируем знач-я 2-х первых критериев.

Если 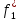<0 иf^*₂<0 , то

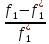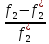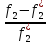>0 и >0 Еслиf₁^*>0 и f₂^*>0 , то <0 и <0.

Поэтому в равенстве относит.отклонений этих критериев модуль абсолютных величин можно опустить. Тогда получим:

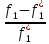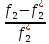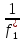= => f₁-1= 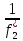f₂-1Введем обознач: d₁=,d₂ = 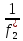=>d₁f₁-d₂f₂=0

Для критериев f₃, f₄ получим точно такое же уравнение, т.к. направления их оптимизации совпадают.Рассмотрим критерии с противоположными направлениями оптимизации f₁и f₃.Если f₁^*<0,

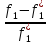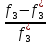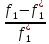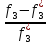f₃^*<0, то >0,<0. Еслиf₁^*>0, f₃^*>0, то <0,>0.

Поэтому при опускании знака модуль перед одним из выражений надопоставить «-». Получим: 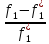= -=>d₁f₁+d₃f₃=2

Т.о., для нахождения компромиссного решения методом равных и наим. относ. отклонений необх. оптимизир-е критерии включить в число неизвестных задачи и к основным ограничениям добавить след. ограничения: d₁f₁-d₂f₂=0 – для всех f_k, кот. как и f₁ максимизир-ся; d₁f₁+d₃f₃=2 - для всех f_k, кот.

36. Метод равных и наим-их относит. Отклонени

Будем решать задачу по к критериям:

max f₁ =

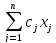
max f₂ =

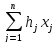
min f_k =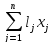 , k=3,k

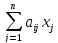( ≤ , = , ≥ ) b_i , i=1,m

x_j ≥ 0, j=1,n

Запишем условия равенства относит.отклонений критериев от их экстримальн.значений.

==…=

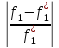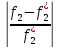Рассмотрим 4 первых критерия. По условию задачи f₁ и f₂ максимизир-ся, а f₃, f₄-минимизир-ся. Проанализируем знач-я 2-х первых критериев.Если

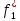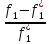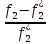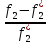<0 и f^*₂<0 , то >0 и>0 Еслиf₁^*>0 и f₂^*>0 , то <0 и <0.

Поэтому в равенстве относит.отклонений этих критериев модуль абсолютных величин можно опустить. Тогда получим:

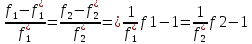
Введем обозначения: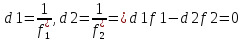

Для критериев f₃, f₄ получим точно такое же уравнение, т.к. направления их оптимизации совпадают.

Рассмотрим критерии с противоположными направлениями оптимизации f₁и f₃.Если f₁^*<0,

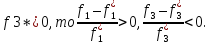
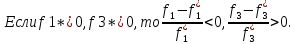
Поэтому при опускании знака модуль перед одним из выражений надо поставить «-». Получим: = -=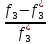>d₁f₁+d₃f₃=2

Т.о., для нахождения компромиссного решения методом равных и наим. относ. отклонений необх. оптимизир-е критерии включить в число неизвестных задачи и к основным ограничениям добавить след. ограничения: d₁f₁-d₂f₂=0 – для всех f_k, кот. как и f₁ максимизир-ся; d₁f₁+d₃f₃=2 - для всех f_k, кот. минимизир-ся. В качестве ЦФ можно взять любую