20. Проверка гипотезы о совпадении уравнений регрессии для двух выборок

Одним из распростран. тестов проверки данной гипотезы явл-ся тест Чоу, суть кот. состоит в след.

Пусть имеются две выборки объемами 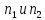.Для кажд. из этих выборок оценено урав-е регр-ии вида:

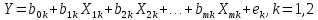
Провер-ся нулевая гипотеза о рав-ве др. другу соотв. коэф-ов регр-ии:

Пусть суммы (k = 1, 2) квадратов отклонений знач-ийот линий регр-ии равны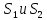соотв-но для 1-ого и 2-ого урав-ий регр-ии.

Пусть по объединенной выборке объема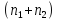оценено еще одно урав-е регр-ии, для кот. сумма квадратов отклоненийот урав-я регр-ии равна.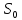

Для проверки Н₀ в этом случае строится след. F-статистика:

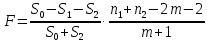
В случае справедливости Н₀ построенная F-статистика имеет распред-ие Фишера с числами степеней свободы .

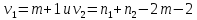Очевидно, F-статистика близка к нулю, если и это фактически означает, что уравнения регрессии для обеих выборок практически одинаковы. В этом случае F < Fкp. Если же F > Fкp., то нулевая гипотеза отклоняется.

21. Статистика Дарбина-Уртсона

Прим-ся для анализа коррелируемости случ. отк-ний. Опр-ся по формуле:

Для больших значений n счит-ся, что , тогда:

=

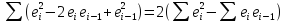
1 случай. Если , то,DW = 0

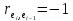2 случай. , то,DW = 4

3 случай.

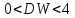
Т.к. абсолютн. значение случ. откл-ний в среднем одинаково, то:

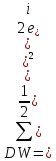
Поэтому необходим. условием незав-ти случ. откл-ний явл-ся близость к 2 значения DW.

“Грубым” правилом можно считать отсутствия автокорр-ции, если 1,5<DW<2,5.

22.Логарифмические (лог-линейные) модели.

Пусть некоторая экономическая зависимость моделируется степенным уравнением:

У=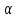Х^β (1), где β и α- параметры модели подлежащие определению.

Функция (1) может отражать зависимость спроса У от его цены Х(β<0) или от дохода Х(β>0,функция Энгеля); зависимость объема выпуска У от использования ресурса Х(0<β<1, производственная функция).

Модель (1) не является линейной функцией относительно Х. производная зависимость переменной У по Х, указывающая на изменение У по отношению к изменению Х, будет зависеть от Х: dY/dX=αβХ^β-1,что присуще нелинейным моделям.

Стандартным и широко используемым подходом к анализу функций данного рода является логарифмирование по экспоненте(е=2,71828).

Прологарифмировав обе части (1), получим:

lnY=lnα+βlnX (2).

Введем замену lnα=β₀ ,β=β₁,тогда (2) примет вид:

lnY=β₀+ β₁ lnХ (3).

С целью статистической оценки коэф. Добавим в модель случайное слагаемое ε и получим двойную логарифмическую модель-зависимая и объясняющая переменные заданы в логарифмическом виде:

lnY=β₀+ β₁ lnХ+ε (4).

Не являясь линейным относительно Х и У, данное уравнение является линейным относительно lnXи lnУ, а также относительно параметров β₀и β₁. Вводя замены lnX=Х^*и lnУ=У^*, (4) можно представить в виде:

У^*=β₀+ β₁Х^*+ε (5).

Модель (5)является линейной моделью. Если выполняются предпосылки классической линейной модели, то по МНК можно определить наилучшие линейные несмещенные оценки коэф. β₀и β₁.

Отметим, что коэф.β₁ определяет эластичность переменной У по переменной Х, т.е.процентное изменение У для данного процентного изменения Х.

В случае парной регрессии обоснованность использования логарифмической модели проверить достаточно просто. Вместо наблюдений (х_i,у_i) рассматриваются наблюдения (lnх_i, lnу_i). Вновь полученные точки наносятся на корреляционное поле. Если их расположение соответствует прямой линии, то произведенная замена удачна и использование логарифмической модели обосновано.

Данная модель данная модель легко обобщается на большее число переменных. Для степенного уравнения m переменных У=αХ₁^β1*…*Х_m^βm двойная логарифмическая модель будет иметь вид:

lnУ= β₀+β₁ lnХ₁+…+β_m lnХ_m+ε, где β₀= lnα.

Здесь коэф.β₁,…, β_m являются эластичностями переменной У по переменным Х₁,…, Х_m соответственно.Часто данная модель используется при анализе производительных функций.

25 - Степенная модель

Степенной моделью называется модель вида Y=β₀+β₁X+β₂X²+…+β_mX^m+ε.

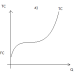
Например, кубическая функция Y=β₀+β₁X+β₂X²+β₃X³+ε в микроэкономике моделирует зависимость издержек TC от объёма выпуска Q (рис. а).

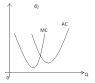
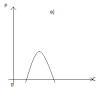
Квадратичная функция (парабола) Y=β₀+β₁X+β₂X² +ε может отражать зависимость между объёмом выпуска Q и средними AC либо предельными MC издержками (рис. б), или между расходами на рекламу C и прибылью P (рис. в) и т.д.

Модель является линейной относительно коэффициентов регрессии β₀, β₁,…β_m.

Следовательно, её можно свести к линейной регрессионной модели. Заменяя X на X₁, X² на X₂, X^m на X_m, получаем модель множественной линейной регрессии с m переменными X₁, X₂,….X_m:

Y=β₀+β₁X₁+β₂X₂+…+β_mX_m+ε.

23/Полулогарифмические модели.

Полулогарифмическими моделями называют модели вида:

lnУ=β₀+ β₁Х+ ε

У= β₀+ β₁ lnХ+ε.

Такие модели обычно используются в тех случаях, когда необходимо определятьтемп роста или прироста каких-либо экономических показателей.

Лог-линейная модель.Рассмотрим зависимость У=У₀ (1+r)^t,

Где У₀ – начальная величина переменной У (начальный капитал), r – процентная ставка, У₁ – значение переменной У в момент времени t. Модель легко сводится к полулогарифмической модели:

lnУ= lnУ₀+ t ln(1+r). обозначим lnУ₀=β₀, ln(1+r)=β₁,тогда:lnУ_t=β₀+ β₁t+ ε_t.

случайное слагаемое ε_t – возможность изменения процентной ставки.

Заменой lnУ_t=У_t* полулогарифмическая модель легко сводится к линейной модели.

Коэф.β₁ имеет смысл темпа прироста переменной У по переменной Х,т.е.характеризует отношение относительного изменения У к абсолютному изменению Х. умножив β₁ на 100, получим процентное изменение переменной У. поэтому полулогарифмическая модель обычно используется для измерения темпа прироста экономических показателей.

Линейно-логарифмическая модель.

Рассмотрим линейно-логарифмическую модель: У= β₀+ β₁ lnХ + ε.

Она сводится к сводится к линейной модели заменой lnX=Х^*.

В данной модели коэф.β₁ определяет изменение переменной У вследствие единичного относительного прироста Х (например на 1%), т.е.характеризует отношение абсолютного изменения У к относительному изменению Х.Данная модель обычно используется в тех случаях, когда необходимо исследовать влияние процентного изменения независимой переменной на абсолютное изменение зависимой переменной.

26 - Показательная модель

Показательная модель: Y=β₀e^β1X

Важным её приложением является ситуация, когда анализируется изменение переменной Y с постоянным темпом прироста во времени. В этом случае переменная X символически заменяется переменной t: Y= β₀e^β1t . Данная функция путём логарифмирования сводится к лог-линейной модели: lnY=lnβ₀+β₁t.

В общем случае Y=β₀a^β1X , где а – произвольная положительная константа, а≠1.

Данная функция сводится к исходной вследствие тождества: a^β1X=e^β1Xlna.

Ряд экономических показателей моделируется через функции, являющиеся композицией перечисленных функции, что позволяет свести их к линейным. Например, производственная функция Кобба-Дугласа с учётом научно-технического рогресса:

Y=AK^aL^βe^γt

Пролагарифмируем данную функцию, получим соотношение:

lnY=lnA+aLnK+βlnL+γt, которое сводится к линейному заменами. lnY=y, lnA=a, lnK=k, lnL=l

27 - Преобразование случайного отклонения

Как отмечалось ранее, для получения качественных оценок существенную роль играет выполнимость предпосылок МНК для случайных отклонений. Наиболее важные из них требуют, чтобы отклонение ε_i, являлись нормально распределёнными случайными величинами с нулевым математическим ожиданием и постоянной дисперсией ϭ², а также не коррелировали друг с другом: ε_i~N(0, ϭ²), cov(ε_i ,ε_j)=0 при i≠j, i,j=1,n. При невыполнимости указанных предпосылок оценки, полученные по МНК, не будут обладать свойствами BLUE-оценок.

В случаях, не требующих совокупного логарифмирования с аддитивным случайным членом, выполнимость предпосылок МНК имеет место, а следовательно, проблем с оцениваем не возникает.

Для описания возможных проблем со случайным отклонением воспользуемся степенной моделью Y=AX^β, выполнив её случайным членом. Рассмотрим три случая:

Y=AX^βe^ε (1)

Y=AX^βε (2)

Y=AX^β+ε (3)

Данные модели являются нелинейными относительно параметра β. Прологарифмировав каждое из этих соотношений, получим:

lnY=lnA+βlnX+ε (4)

lnY=lnA+βlnX+lnε (5)

lnY=ln(AX^β+ ε) (6)

Использование (4) для оценки параметров в (1) не вызывает осложнений, связанных со случайным отклонением.

Преобразование (2) в (5) приводит к преобразованию случайных отклонений ε_i в ln ε_i . Использование МНК в (5) для нахождения BLUE-оценок параметров требует, чтобы отклонение v_i= ln ε_i, удовлетворяли предпосылкам МНК: v_i~ N(0, ϭ²). Но это возможно только в случае логарифмически нормального распределения СВ ε_i с M(ε_i)=e^ ϭ²/2 и D(ε_i)= e^ ϭ²(e^ ϭ²-1) .

Логарифмирование соотношения (6) не приводит к линеаризации соотношения относительно параметров. В этом случае для нахождения оценок необходимо использовать определённые интерационные процедуры оценки нелинейных регрессий.

Таким образом, при использовании преобразований с целью нахождения оценок необходимо особое внимание уделять рассмотрению свойств случайных отклонений, чтобы полученные в результате оценки имели высокую статистическую значимость.

30 – Постановка и мат. модель задачи векторной оптимизации

Многие экономико-управленческие задачи являються многоцелевыми, в силу этого решение по одному критерию может оказаться не наилучшим по другим. Для решен подобн задач исп метод векторн оптимизац.

Множество критериев можно представить в виде векторной целевой ф-ии:

F(x) = (f₁(x)f₂(x),…, f_k(x))

Для минимизации частного критерия f_k(x) достаточно максимизировать - f_k(x), т. к.

min f_k(x) = max (-f_k(x)), поэтому каждый компонент векторного критерия максимизируется.

Задача: 1. max F (x) = (f₁(x)f₂(x),…, f_k(x))

2. φ_i(x) {<=,=,>=}b, i= 1,n

3. x_ij >=0, j=1,n

Будем рассматривать эту задачу для случая, когда оптимальные решения x_k, k= 1,k, полученные при решении по каждому критерию не совпадают. Найти решения, при которых значения всех критериев одновременно будет наилучшим можно в области компромисса, кот в ОДР.

Решения, которые доставляют критериям наилучшие значения называются – эффективными, компромиссными, оптимальными по Паретто.

План Х₁ не хуже плана Х₂, если f_k(x₁)>=f_k(x₂), k=1,n. Если среди последних неравенств хотя бы одно строгое, то план Х₁ называется предпочтительнее плана Х_2./ План Х₁ оптимален по Паретто, если он допустим и не существует другого плана Х₂, для которого f_k(x₁)>=f_k(x₂), k=1,n и хотя бы для 1-го критерия выполняется строгое неравенство.

31 – Основные проблемы, возникающие при решении задач векторной оптимизации.

Проблема нормализации. Возникает в связи с тем, что локальные критерии имеют различные ед-цы и масштабы измерения, что делает невозможным их непосредственное сравнение. Для этого приходится приводить их к единому масштабу и безразмерному виду – нормировать. Самые распространённые способы нормирования: - замена абсолютных значений критериев их безразмерными относительными величинами: f_k = f_k/f*_k, k=1,n; - замена абсолютных значений критериев их относительными значениями отклонений от оптимальных значений

1. Проблема учёта приоритетов критерия. Здесь приходится находить как математическое, так и специальное влияние критерия на решение задачи.

2. Проблема определения области компромисса.

32 – методы решения многоцелевых задач

Методы решения многоцелевых задач делятся на:

-методы, кот основаны на свёртывании критериев -методы, в кот используются ограничения на критерии, -методы, которые основаны на отыскании компромиссного решения.

Наиболее распространёнными среди них являются:

1.Метод линейной комбинации частных критериев 2.Метод оследовательных уступок 3.Метод ведущего критерия 4.Метод равных и наименьших относительных отклонений