2.9. Векторное пространство

Для построения общей теории систем линейных уравнений не достаточно рассмотренного нами ранее аппарата. Помимо определителей и матриц, в теории используется еще одно понятие, представляющее, быть может, еще больший общематематический интерес, а именно понятие многомерного векторного пространства.

Известно, что всякая точка плоскости определяется (при заданных осях координат) своими двумя координатами, т.е. упорядоченным набором двух действительных чисел; всякий вектор на плоскости определяется своими двумя компонентами, т.е. снова упорядоченным набором двух действительных чисел. Аналогично всякая точка трехмерного пространства и всякий вектор в нем определяются упорядоченным набором трех действительных чисел.

В геометрии, а также в механике и физике часто приходится, однако, изучать такие объекты, для задания которых недостаточно трех действительных чисел. Так, рассмотрим совокупность шаров в трехмерном пространстве. Для того, чтобы шар был полностью определен, надо задать координаты его центра и радиус, т.е. задать упорядоченный набор четырех действительных чисел, из которых, впрочем, последнее (радиус) может принимать лишь положительные значения. Рассмотрим, с другой стороны, различные положения твердого тела в пространстве. Положение тела будет вполне определено, если будут указаны координаты его центра тяжести (три действительных числа), направление некоторой фиксированной оси, проходящей через центр тяжести (два числа - два из трех направляющих косинусов), и наконец, угол поворота вокруг этой оси. Таким образом, положение твердого тела в пространстве определяется упорядоченным набором из шести действительных чисел. Эти примеры указывают на целесообразность рассмотрения совокупности всевозможных упорядоченных наборов из n действительных чисел. Эта совокупность после введения в нее операций сложения и умножения на число (что мы сделаем ниже) и носит название n-мерного векторного пространства. Таким образом, n-мерное векторное пространство есть лишь алгебраическое образование, сохраняющее некоторые простейшие свойства совокупности векторов трехмерного пространства, выходящих из начала координат.

 Упорядоченный набор n чисел

 (2.34)

называется 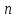-мерным вектором. Числа  называются компонентами (координатами) вектора.

Для обозначения векторов будем использовать курсив.

Векторы и

 (2.35)

называются равными в том и только том случае, если совпадают их компоненты, стоящие на одинаковых местах, т.е. если

при .

В качестве примеров векторов укажем следующие:

1. Векторы - отрезки, выходящие из начала координат на плоскости или в трехмерном пространстве, будут при фиксированной системе координат соответственно двух - и трехмерными векторами в смысле данного выше определения,

2. Коэффициенты всякого линейного уравнения с n неизвестными составляют n-мерный вектор.

3. Всякое решение любой системы линейных уравнений с n неизвестными будет n-мерным вектором.

4. Если дана матрица из s строк и n столбцов, то ее строки будут n-мерными векторами, столбцы - s-мерными векторами.

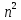5. Сама матрица размерами может рассматриваться как-мерный вектор: достаточно прочесть элементы матрицы подряд, строчку за строчкой; в частности, каждая квадратная матрица порядкаможет рассматриваться как-мерный вектор, причем, очевидно, всякий-мерный вектор может быть получен этим путем из некоторой квадратной матрицы порядка.

 Суммой векторов  (2.34)  и  (2.35)  называется вектор

 , (2.36)

компоненты которого суть суммы соответствующих компонент слагаемых векторов.

Сложение векторов коммутативно и ассоциативно ввиду коммутативности и ассоциативности операции сложения чисел.

Роль нуля играет нулевой вектор :

= .

Действительно,  

Назовем противоположным  вектору (2.34) вектор

.

Очевидно, что  . Теперь легко видеть, что для сложения векторов существует обратная операция - вычитание векторов:разностью векторов  (2.34)  и (2.35)  называется вектор

= .

Сложение -мерных векторов, определяемое формулой (2.36), возникло из сложения векторов на плоскости и в трехмерном пространстве. На плоскости и в трехмерном пространстве используется так же умножение вектора на действительное число (на скаляр): умножение векторана числоозначает прирастяжение  векторавраз (сжатие при), а прирастяжение враз и изменение направления на противоположное. Переходя к общему случаю, мы получаем определение:

 произведением вектора  (2.34) 1 на число  называется вектор

,

компоненты которого равны произведению на соответствующих  компонент вектора.

Из этого определения вытекают следующие важные свойства:

;

;

;

.

Эти свойства непосредственно следуют из определение операций сложения и умножения на число.

Столь же легко проверяются следующие свойства:

;

;

;

если  то или, или.

Совокупность всех -мерных векторов с действительными компонентами, рассматриваемая с определенными в ней операциями сложения векторов и умножения вектора на действительное число, называетсямерным векторным пространством.

Так, векторы-отрезки, выходящие из начала координат на плоскости или в трехмерном пространстве, составляют при фиксированной системе координат двумерное и, соответственно, трехмерное векторные пространства.

Рассмотрим еще один пример. Левая часть линейного уравнения от неизвестных, т.е. выражение вида

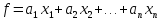
называется линейной формой от неизвестных . Линейная формавполне определяется векторомиз своих коэффициентов; обратно, всякий -мерный вектор однозначно определяет некоторую линейную форму. Сложение векторов и умножение вектора на число превращаются в соответствующие операции над линейными формами; эти операции широко нами использовались при рассмотрении метода Гаусса.

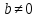Вектор  называетсяпропорциональным вектору  , если существует такое число, чтоВ частности, нулевой вектор пропорционален любому вектору ввиду равенства. Если жеи, откуда, то, т.е. для ненулевых векторов пропорциональность обладает свойством симметричности.

Обобщим понятие пропорциональности.

Вектор  называетсялинейной комбинацией векторов  , если существуют такие числа,, …,, что

.

Таким образом, j-я компонента вектора   равна

.

Система векторов

  (2.37)

называется линейно зависимой, если хотя бы один из них является линейной комбинацией остальных векторов системы (2.37), и линейно независимой  - в противоположном случае.

Дадим другую форму этого весьма важного определения: система векторов (2.37) линейно зависима, если существуют такие числа ,, …,, хотя бы одно из которых отлично от нуля, что имеет место равенство

(2.38)

Докажем эквивалентность этих двух определений. Пусть, например, вектор  из системы векторов (2.37) есть линейная комбинация остальных векторов, тогда

.

Отсюда вытекает равенство  т.е. равенство вида (2.38), при этом коэффициент приравенОбратно, пусть векторы (2.37) связаны соотношением (2.38), в котором, например,Тогда

т.е. вектор оказался линейной комбинацией векторов.

Второе из данных определений применимо и в случае r=1.

Подсистемой системы векторов  (2.37) назовем любой набор векторов, каждый из которых входит в систему (2.37).

Имеет место следующее утверждение.

Если некоторая подсистема системы векторов  (2.37)  линейно зависима, то и вся система  (2.37)  линейно зависима.

Из этого свойства вытекает линейная зависимость всякой системы векторов, содержащей два одинаковых вектора, или, более обще, два пропорциональных вектора, а так же всякой системы, содержащей нулевой вектор.

Сколько же векторов может содержать линейно независимая система -мерных векторов? Для ответа на эти вопросы рассмотрим в-мерном векторном пространстве векторы

),

,

. . . . . (2.39)

,

называемые единичными векторами  этого пространства. Система единичных векторов линейно независима: пусть

;

так как левая часть этого равенства равна вектору , то

,

т.е.  , так как все компоненты нулевого вектора равны нулю.

Мы нашли в n-мерном векторном пространстве одну линейно независимую систему, состоящую из векторов.

Теорема 2.4. Всякие векторов-мерного векторного  пространства составляют при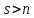линейно зависимую систему.

Пусть нам даны векторы

,

,

. . . .

.

Нам надо подобрать такие числа , не все равные нулю, что

. (2.40)

Переходя от равенства (2.40) к соответствующим равенствам между компонентами, получаем

. . . . . . (2.41)

Равенства (2.41) образуют систему однородных линейных уравнений относительнонеизвестных. Число уравнений в этой системе меньше числа неизвестных, а решение она имеет (нулевое), т.е. она совместная, значит она имеет и ненулевое решение. Таким образом, можно подобрать такие, что не все они равны нулю одновременно и удовлетворяют соотношению (2.40).

Назовем линейно независимую систему векторов

 (2.42)

максимальной линейно независимой системой,  если добавление к ней любого -мерного векторадает уже линейно зависимую систему. Так как во всякой линейной зависимости, связывающей векторы, коэффициент придолжен быть отличным от нуля - иначе система (2.42) была бы линейно зависимой, - то векторлинейно выражается через векторы (2.42). Поэтому система векторов (2.42) тогда и только тогда будет максимальной линейно независимой системой, если система векторов (2.42) линейно независима, а любой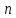-мерный векторявляется их линейной комбинацией. Отсюда вытекает, что  в-мерном пространстве  всякая линейно независимая система извекторов будет максимальной, и что любая максимальная линейно независимая система векторов этого пространства состоит не более чем из n векторов.

Очевидно, что всякая линейно независимая система мерных векторов содержится хотя бы в одной максимальной линейно независимой системе. Так как система, состоящая из одного ненулевого вектора, линейно независима, то мы получаем, что всякий ненулевой вектор содержится в некоторой максимальной линейно независимой системе, а поэтому в-мерном векторном пространстве существует бесконечно много различных максимальных линейно независимых систем векторов.

Оказывается (доказательство мы опускаем), что в -мерном векторном пространстве не существует максимальных линейно независимых систем с числом векторов в них меньшим.

Определение -мерного векторного пространства начиналось с определения-мерного вектора как упорядоченной системы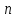чисел (координат). Целесообразно дать "бескоординатное" определение векторного пространства.

Такое определение вводится аксиоматически, в нем ничего не говорится о свойствах отдельного вектора, но перечисляются те свойства, которым должны удовлетворять операции над ними.

Пусть дано множество ; его элементы будем обозначать малыми латинскими буквами. Пусть в множествеопределена  операция сложения, ставящая в соответствие каждой паре элементоводнозначно определенный элемент, называемый их суммой и обозначаемый, и  операция умножения на действительное число, ставящая в соответствие каждому элементуи действительному числуоднозначно определенный элемент, обозначаемыйи называемый произведениемна.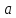

Элементы множества будем называтьвекторами , а само множество действительным линейным пространством,  если указанные операции обладают следующими свойствами:

1. Сложение коммутативно:  

2. Сложение ассоциативно: .

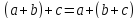3. В существует  нулевой элемент, удовлетворяющий условию:0 для всякого.

Легко доказывается единственность нулевого элемента.

4. Для всякого элемента  существует  противоположный элемент, удовлетворяющий условию:.

Заметим, что противоположный элемент единственный.

Из перечисленных аксиом выводится существование и единственность разности т.е. такого элемента.

Следующие аксиомы касаются умножения элементов из на числа. Для любых элементов, любых действительных чисели действительного числадолжны выполняться равенства:

5. 

Примерами действительных линейных пространств являются -мерные действительные векторные пространства, рассмотренные в начале параграфа. Существуют примеры бесконечномерных линейных пространств: множества бесконечных последовательностей действительных чисел с естественным образом введенными операциями сложения и умножения на число; множество действительных функций одной переменной, заданных на отрезкеи т.д.

Для линейных пространств вводятся понятия линейной зависимости и независимости системы векторов, понятие максимальной линейно независимой системы, что позволяет перейти к координатной форме задания элементов множества и обобщить соответствующие результаты, полученные в теории векторных пространств. Но понятие-мерного линейного пространства не в полной мере обобщает понятия плоскости или трехмерного пространства. В линейном пространстве не определены ни длина вектора, ни угол между векторами. Поэтому в нем не возможно развитие той богатой геометрической теории, которая хорошо знакома читателю для плоскости и пространства.

Рассматривая в следующей главе элементы векторной алгебры, в которой под вектором понимается направленный отрезок на плоскости или в трехмерном пространстве, мы познакомимся с понятием скалярного произведения двух векторов, которое равно произведению длин векторов-сомножителей на косинус угла между ними. Там же доказывается, что скалярное произведение равно сумме произведений соответствующих координат сомножителей: если  и   то

.

Оказывается, что длина вектора  обозначаемая, выражается через скалярное произведение:

, (2.43)

а косинус угла  между векторамиидается формулой:

Воспользуемся этими соображениями и введем в -мерном линейном пространствескалярное произведение.

Будем говорить, что в пространстве определено скалярное произведение, если всякой паре векторовизпоставлено в соответствие действительное число, обозначаемое символоми называемое скалярным произведением векторов, причем выполняются следующие условия (здесьпроизвольные векторы из,- любое действительное число):

1

2.

3. .

4. Если  , то(скалярный квадрат вектора, отличного от нулевого, строго больше нуля).

Если в -мерном линейном пространстве определено скалярное произведение, то оно называется-мерным евклидовым пространством  и обозначается .

Любое -мерное линейное пространство можно превратить в евклидово, положив

 .

где   и  .

Введя скалярное произведение, мы получили возможность говорить о длине векторов и об углах между ними, которые вычисляются по формулам, аналогичным (2.43), (2.44).

По аналогии с геометрией на плоскости и в пространстве будем называть векторы  иортогональными, если их скалярное произведение равно нулю (угол между ними прямой, если, конечно, среди них нет нулевого). Система векторов называется  ортогональной системой, если все векторы этой системы попарно ортогональны, всякая такая система линейно независима.

Система векторов называется ортонормированной,  если она ортогональная и длина каждого из ее векторов равна единице.

Максимальной линейно независимой ортонормированной системой векторов в -мерном евклидовом пространстве является система (2.39), которая, как правило, и используется для задания системы координат в этом пространстве.

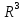Евклидовыми пространствами иявляются соответственно плоскость и пространство с заданными в них декартовыми системами координат.

На этом мы заканчиваем рассмотрение вопросов линейной алгебры. Желающих расширить свой кругозор в этой области математики мы отсылает к литературе (см. [3-6]).