4.2. Различные формы уравнения прямой на плоскости

Ранее было показано, что, выбрав определенную систему координат на плоскости, мы можем геометрическое свойство, характеризующее точки рассматриваемой линии, выразить аналитически уравнением между текущими координатами. Изучим теперь более внимательно уравнения прямых линий (прямых).

Чтобы составить уравнение прямой в декартовых координатах, надо каким-то образом задать условия, определяющие ее положение относительно координатных осей.

Назовем углом наклона прямой к оси Ox  угол, на который нужно повернуть ось Ox, чтобы она совпала с данной прямой (или оказалась параллельна ей). Этот угол будем рассматривать с учетом знака (он определяется направлением поворота: против или по часовой стрелке). Добавочный поворот оси на снова совместит ее с прямой, т.е. угол наклона прямой к оси Ox определен не однозначно. Его же тангенс определяется однозначно.

Тангенс угла наклона прямой к оси Ox называется угловым  коэффициентом прямой.

Угловой коэффициент характеризует направление прямой (мы здесь не различаем двух взаимно противоположных направлений прямой). Если угловой коэффициент прямой равен нулю, то прямая параллельна оси абсцисс. Заметим, что прямая, перпендикулярная к оси Ox, не имеет углового коэффициента.

Рассмотрим прямую, не параллельную оси ординат. Ее положение на плоскости будет вполне определено, если задать угол ее наклона к оси абсцисс и величину отрезка, отсекаемого ею на оси ординат, т.е. величину направленного отрезка (рис.4.2).

Рис.4.2. Уравнение прямой с угловым коэффициентом.

Рассмотрим направленный отрезок . Координаты его начала и конца естьи, тогда, отсюда, полагая, получаемили

. (4.2)

Этому уравнению удовлетворяют лишь координаты точек рассматриваемой прямой; оно нарушается, если точка не лежит на прямой. Таким образом, полученное уравнение является уравнением заданной прямой линии. Оно называется уравнением прямой с угловым коэффициентом. 

Пусть прямая теперь параллельна оси Oy, и пусть - абсцисса точки пересечения этой прямой с осью Ox (рис.4.3). Очевидно, что любая точка прямой имеет абсциссу, равную; если же точка не лежит на прямой, то ее абсцисса будет отлична от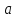. Следовательно, рассматриваемая прямая имеет уравнение

(4.3)

Так как уравнения (4.2) и (4.3) являются уравнениями первой степени относительно переменных то тем самым мы доказали, что в декартовой системе координат всякая прямая может быть представлена уравнением первой степени.

В частности, если прямая проходит через начало координат, то и ее уравнение будет иметь вид:.

Если прямая параллельна оси абсцисс, то ее угловой , и уравнение прямой будет.

Рассмотрим теперь уравнение первой степени общего вида:

. (4.4)

(здесь - произвольные числа; при этом конечно, коэффициенты при переменных не могут одновременно равняться нулю иначе (4.4) не было бы уравнением). Покажем, что это уравнение определяет прямую. Установим, геометрическое место точек плоскости, координаты которых удовлетворяют этому уравнению.

Разрешим уравнение (4.4) относительно , предполагая, что. Получим:

,

где . Но это есть уравнение прямой с угловым коэффициентом.

Мы предполагали, что . Если жето уравнение (4.4) примет вид. Решая его относительно x, получим:, откуда, вводя обозначениебудем иметь:. Но, как мы видели ранее, это есть уравнением прямой, параллельной оси ординат.

 Таким образом, мы показали, что  всякое уравнение первой степени относительно текущих координат определяет прямую.  Поэтому уравнение (4.4) называется общим уравнением прямой. 

Подводя итог, мы можем сказать, что прямая, и только она, может быть представлена в декартовой системе координат уравнением первой степени относительно текущих координат

Заметим, что для приведения уравнения первой степени к виду (4.2) нужно решить его относительно . Тогда коэффициент прив таком уравнении будет угловым коэффициентом прямой, а свободный член будет давать величину отрезка, отсекаемого прямой на оси ординат. Этот вид уравнения прямой особенно важен: график линейной функции отто есть многочлена первой степени, есть прямая линия, и обратно, если графиком некоторой функции отявляется прямая, то эта функция может быть записана в виде многочлена первой степени от. Отсюда происходит название: линейная функция ("прямолинейная").

Пример 4.5. Написать уравнение с угловым коэффициентом для прямой, заданной уравнением Решая это уравнение относительно, получим:

Посмотрим, какое положение занимает прямая, когда один или два коэффициента в уравнении (4.4) обращаются в нуль.

1. . В этом случае уравнение (4.4) имеет вид:и определяет прямую, проходящую через начало координат, так как это уравнение удовлетворяется при.

2. При получаем:Эта прямая параллельна оси абсцисс и проходит через точку

3. При . Эта прямая, параллельна оси ординат и проходит через точку

4. При C=B=0 уравнение (4.4) принимает вид: Ax=0 или x=0, и прямая совпадает с осью ординат.

5. При C=A=0 уравнение (4.4) приводится к виду , и прямая совпадает с осью абсцисс.

Мы уже говорили, что положение прямой по отношению к осям координат можно определить различными способами. В зависимости т этого будем получать различные формы ее уравнения.

Пусть нам известно, что искомая прямая проходит через точкуи перпендикулярна вектору(рис.4.4). Рассмотрим текущую точкуна этой прямой и вектор. Из условия следует, что он перпендикулярен вектору, т.е. скалярное произ-

ведение . Так как, то мы получаем, что для любой точки прямой должно выполняться уравнение:

или

. (4.5)

Рассмотрим прямую, пересекающую обе координатные оси и не проходящую через начало координат. Ее положение можно определить, указав величины a и b отрезков, отсекаемых прямой соответственно на осях Ox и Oy (рис. 4.5).

Уравнение этой прямой можно записать в виде где ни один из коэффициентов не равен нулю. Обозначим через M и N точки пересечения данной прямой с осями координат, тогда для точки M имеем:, т.е.; для точки N:Подставляя эти значения дляв исходное уравнение, получаем:. Деля обе части этого уравнения на(по предположению), найдем, что-x/a-y/b+1=0, или

. (4.6)

Уравнение прямой, записанное в форме (4.6), называется уравнением в отрезках.

Пример 4.6. Уравнение прямой написать в отрезках.

Найдем координаты точек пересечения рассматриваемой прямой с осями координат: так как точка лежит на этой прямой, то, откудалежит на прямой, то. Тогда искомое уравнение будет

.

Чтобы построить прямую, достаточно нанести на чертеж две какие-нибудь ее точки. Для отыскания координат точки, лежащей на прямой, выбираем произвольное значение одной из координат и по уравнению прямой находим соответствующее значение второй из координат. Лучше выбирать точки на осях координат.

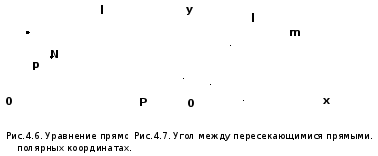
Пример 4.7. Построить прямую, имеющую уравнение 2x-y-3=0.

Положим, например, Следовательно, точка (1;-1) лежит на прямой. Аналогично, полагая, например,также лежащую на прямой.

Рассмотрим полярную систему координат. Положение прямой на плоскости будет вполне определено, если задать ее расстояние и уголмежду полярной осью и осью, проходящей через полюс перпендикулярно к рассматриваемой прямой (рис. 4.6). Положительным направлением осибудем считать направление от полюса к данной прямой (если прямая проходит через полюс, то положительное направление осиможет быть выбрано любым). Очевидно, что все точки прямой и только они обладают свойством: проекция на осьвектора, проведенного из полюса в точку M прямой линии, равна. 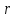Обозначим черезиполярные координаты точки на рассматриваемой прямой, тогда

.

Мы получили  уравнение прямой в полярных координатах.