5.5. Основные задачи о положении прямой

Рассмотрим теперь некоторые задачи о положении прямой.

Углом между прямыми в пространстве называется любой из  углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным прямым. При этом условимся брать угол в пределах от 0 до  .

Рассмотрим уравнения двух прямых:

очевидно, за угол  между ними можно принять угол между их направляющими векторамииили угол, дополняющий его до. Поэтому

в формуле (5.27) можно брать любой знак, что соответствует выбору одного из двух различных углов между данными прямыми.

Пример 5.12. Найти угол между прямыми /(-1). Для первой прямой направляющие коэффициенты будут:,,, а для второй:,,. Следовательно:

Откуда или.

Для перпендикулярных прямых =0, и из формулы (5.27) мы получаемусловие перпендикулярности двух прямых: 

.

Условием параллельности прямых  будет выполнение равенств:

.

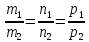Это условие можно получить, заметив, что направляющие векторы прямых коллинеарны.

Рассмотрим задачу о нахождении уравнений прямой, проходящей через две заданные точки  и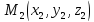. Будем искать эти уравнения в канонической форме.

Для решения задачи достаточно знать координаты одной из точек, лежащих на прямой, и направляющий вектор. Возьмем, например, точку . За направляющий же вектор прямой примем вектор. Проекции его на координатные оси равны

.

Уравнения искомой прямой примут вид:

5.6. Задачи на взаимное расположение прямой и плоскости

Пусть прямая и плоскость заданы уравнениями::

(5.28)

Найдем угол между ними. Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Найдем синус этого угла , при этом в дальнейшем будем считать, что, потому что синусы смежных углов равны. Уголбудет углом между прямой и перпендикуляром к плоскости. Его косинус найдем по координатамнормали к плоскости и координатамнаправляющего вектора данной прямой; так как, то мы получим

Числитель берется по абсолютной величине, так как

В случае параллельности прямой и плоскости: угол между ними равен нулю, следовательно, , и формула (5.29) дает необходимое и достаточное условие параллельности:.

Условие перпендикулярности прямой и плоскости  0совпадает с условием параллельности этой прямой и перпендикуляра к плоскости: .

Найдем теперь координаты точки пересечения прямой с плоскостью, для чего надо совместно решить уравнения (5.28).

Так как все три отношения в уравнениях прямой равны, то мы можем эти уравнения записать в виде:

где - неизвестный параметр. В результате мы получим четыре уравнения первой степени с четырьмя неизвестными:

Из первых трех уравнений находим:

(5.30)

Подставляя эти значения в четвертое уравнение, получаем:

или

,

откуда находим:

.

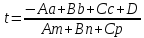Подставляя найденное значение в формулы (5.30), найдем координаты искомой точки. Если, тоимеет определенное конечное значение; следовательно, в этом случае прямая пересекает плоскость в одной точке.

В случае, когда ипрямая параллельна плоскости (в силу первого равенства), а точкачерез которую проходит прямая, лежит вне плоскости, следовательно, прямая не имеет общих точек с плоскостью.

Если то прямая параллельна данной плоскости и проходит через точкулежащую в этой плоскости (в силу второго равенства), следовательно прямая вся лежит в данной плоскости.

Рассмотрим две прямые, заданные уравнениями:

Обозначим направляющий вектор первой из них через  , второй - через. Как видно из уравнений прямых, первая из них проходит через точкус радиусом-вектором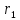, вторая - через точкус радиусом-вектором. Рассмотрим вектор, его проекциями будут:. Из геометрических соображений ясно, что данные прямые лежат в одной плоскости в том и только том случае, если три векторакомпланарны. Следовательно, искомое условие принадлежности двух прямых плоскости заключается в равенстве нулю смешанного произведения этих трех векторов:

или, в проекциях:

.