5.3. Основные задачи о положении плоскости

Пусть уравнения двух данных плоскостей будут

и .

Углом между двумя плоскостями  называется любой из двух смежных двугранных углов, образованных этими плоскостями (в случае параллельности плоскостей угол между ними можно считать равным или по желанию). Один из этих двугранных углов равен углумежду нормалями () и () к данным плоскостям (рис.5.5). Он определяется по известной формуле:

В случае перпендикулярности двух рассматриваемых плоскостей угол между ними равен , т.е.. Поэтому из формулы (5.15) получаемусловие перпендикулярности плоскостей

(5.16)

Условие параллельности плоскостей  в векторной форме может быть записано так: , гдеи- нормали к данным плоскостям. Переходя к проекциям, перепишем это условие в виде:

, что равносильно условию

Пример 5.7. Показать, что плоскост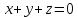и иперпендикулярны между собой. Условие перпендикулярности здесь выполняется:

.

Составим  уравнение плоскости, проходящей через данную точку параллельно данной плоскости.  Пусть даны точка и плоскость, заданная уравнениемНапишем уравнение произвольной плоскости, проходящей через данную точку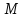:. Чтобы эта плоскость была параллельна данной плоскости, нужно выполнить условие:Следовательно, можно взять. Подставляя эти значения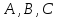в уравнение плоскости, получим искомое уравнение:

. (5.17)

Пример 5.8. Составить уравнение плоскости, проходящей через начало координат параллельно плоскости . Здесь. Следовательно, с учетом (5.17) уравнение искомой плоскости будет:.

Составим  уравнение плоскости, проходящей через две данные точки перпендикулярно к данной плоскости. Пусть даны две точки ,и плоскость. Уравнение плоскости, проходящей через точку, имеет вид:

. (5.18)

Условиями прохождения этой плоскости через точку и перпендикулярности к данной плоскости будут:

(5.19)

Остается выразить из (5.19) отношения двух каких-то коэффициентов к третьему и подставить их в уравнение (5.19).

Пример 5.9. Составить уравнение плоскости, проходящей через точки (1;1;1) и (4;2;-1) перпендикулярно к плоскости . Уравнение плоскости, проходящей через первую точку:

. (5.20)

Условиями прохождения этой плоскости через вторую точку и перпендикулярности к данной плоскости являются: Откудаи. Отсюда находим, что. Разделив уравнение (5.20) наи подставив в него найденные значения для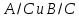получим:

или

.

Это и есть уравнение искомой плоскости.

Рассмотрим задачу об определении расстояния от точки до плоскости.

Отклонением данной точки от данной плоскости  называется длина перпендикуляра, опущенного из этой точки на плоскость, взятая со знаком плюс, если точка и начало координат лежат по разные стороны от данной плоскости, и со знаком минус, если они лежат по одну сторону от плоскости; для точек, лежащих на плоскости, отклонение равно нулю.  Расстояние от точки до плоскости  равно абсолютной величине отклонения.

Пусть требуется найти расстояние от данной точки , имеющей радиус-вектор, до плоскости, заданной нормальным векторным уравнением(рис.5.6).

Вектор параллелен единичному вектору, следовательно,. Множитель, взятый по абсолютной величине, дает искомое расстояние. Знак жебудет положительным, если векторы имеют одинаковое направление, и отрицательным, если их направления противоположны, т.е. d есть отклонение от плоскости.

Заметив это, из рис.5.6 усматриваем, что или.  Так как, с другой стороны, точкалежит на плоскости, то радиус-векторэтой точки должен удовлетворять уравнению этой плоскости, т.е.или, откуда

Выражая скалярное произведение  через проекции сомножителей, получим в координатах

,

т.е. чтобы найти отклонение точки от плоскости, надо в левую часть ее нормального уравнения в канонической форме подставить вместо текущих координат координаты данной точки. Расстояние от точки до плоскости равно абсолютной величине отклонения.

Пример 5.10. Найти расстояние от точки (1;2;3) до плоскости . Напишем нормальное уравнение этой плоскости, умножив данное уравнение на нормирующий множитель

получим: . Отклонение точки от плоскости равно

.

Знак минус означает, что данная точка и начало координат лежат по одну сторону от данной плоскости. Искомое расстояние равно 2/3.