3.3. Скалярное произведение векторов

В механике и физике часто приходится иметь дело со следующей задачей: найти работу силы , если точка, на которую действует эта сила, совершает перемещение, равное вектору.

Если точка движется по направлению силы, то, работа силы равна произведению величины силы на длину перемещения. Если же точка движется под углом к направлению силы, то работает только та составляющая силы, направление которой совпадает с направлением перемещения. Проектируя силу на это направление, получаем:. Следовательно, работа силы будет равна:По двум данным вектораммы определили скаляр, называемый скалярным произведением этих векторов.

 Скалярным произведением векторов a и b называют число,  равное произведению их модулей на косинус угла между ними. Обозначать скалярное произведение векторов будем через:

 (3.9)

Свойства скалярного произведения.

1) Скалярное произведение коммутативно, т.е.  .

2)  

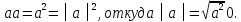
3)   тогда и только тогда, когда векторы  ортогональны или хотя бы один из них равен нулю.

Эти свойства вытекают непосредственно из определения.

4) Скалярное произведение двух векторов равно произведению модуля одного на проекцию другого на направление первого, то есть .

Это вытекает из определений скалярного произведения и проекции вектора на ось.

5) Для любых векторов  и любых чиселивыполнено равенство (распределительный закон):

, в частности и.

  6) Скалярное произведение векторов равно сумме произведений их соответствующих координат: если  ито

 (3.10)

Действительно,  b тогда

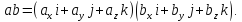
Используя распределительный закон, получаем, что

Последнее равенство получилось так, как  .

7) Косинус угла между двумя векторами  0 равен:

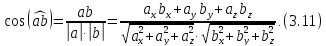Отметим, что для перпендикулярности векторовнеобходимо и достаточно чтобы выполнялось условие:

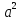Пример 3.8. Векторы ,4. Найти а) , б)  , в) .

Имеем:   a)  б) 

в) (3

Пример 3.9. Векторы образуют угол; зная, чтоугол между векторами.

Имеем:  . Воспользуемся равенством (3.11):

3.4. Векторное произведение двух векторов

Векторным произведением двух называется вектор, длина которого равна площади параллелограмма, построенного на векторах,  перпендикулярный к плоскости этих векторов и направленный так, чтобы кратчайший поворот отвокруг полученного векторапредставлялся происходящим против часовой стрелки, если смотреть из конца вектора(рис.3.13).

Из этого определения следует, что длина вектора  равна:

 . (3.12)

Векторное произведение Векторное произведение равно нулевому вектору в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы параллельны,  т.е. если векторы коллинеарны.

Таким образом, условием коллинеарности векторов будет:

. (3.13)

В частности, всегда  .

Замечание 3.2. Условие (3.13) коллинеарности двух векторов можно заменить следующим:, где-некоторое число (считая).

Если векторы a и b взаимно перпендикулярны, то sin( )=1, и, значит, длина вектора-произведения равна произведению длин векторов сомножителей, т.е. в этом случае

Пример 3.10. Проверить справедливость равенства .

Векторы  направлены по осям координат Ox и Oy, тогда векторбудет направлен по оси Oz. С другой стороны, его длина равна площади прямоугольника, построенного на векторах, т.е. 1. Следовательно,.

Отметим, что аналогично доказывается, что

.

Пример 3.11. Показать, что

Действительно,

 складывая эти два равенства, находим:

.

В механике важное значение имеет понятие момента относительно данной точки. Если силаприложена к точке A (рис. 3.14), то моментом силыотносительно точки O называется вектор, определяемый формулой

,

где есть радиус-вектор точки приложения. Из определения векторного произведения следует, что величина момента равна величине силы, умноженной на расстояние OP точки O от прямой, вдоль которой действует сила ( расстоянием от точки до прямой называется длина перпендикуляра, опущенного из точки на прямую).

Свойства векторного произведения.

1. При перестановке сомножителей векторное произведение умножается на (-1), т.е.  .

В самом деле, площадь параллелограмма, построенного на векторах 2  , не меняется при перестановке. Поэтому векторыиимеют одинаковые длины и коллинеарны. Их же направления противоположны.

2. , т.е. чтобы умножить векторное произведение векторов на число, достаточно умножить на это число один из сомножителей.

3.Векторное произведение подчиняется распределительному (дистрибутивному) закону, т.е. .

Для доказательства заметим сначала, что произведение  a, где  - единичный вектор (), можно построить так (рис.3.15а). Спроектируем векторна плоскость, перпендикулярную к, и полученную вектор-проекцию, повернем в этой плоскости вокруг точкипо часовой стрелке на(если смотреть на плоскость с конца вектора).

Полученный вектор и равенВ самом деле,

,

где  -угол между векторами; векторперпендикулярен к векторамии направлен в ту сторону, из которой кратчайший поворот откпредставляется совершающимся против часовой стрелки. Итак,.

Пусть теперь даны единичный вектор  , перпендикулярная к нему плоскостьи треугольник(рис.3.16б), в котором

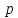Спроектируем треугольник на плоскостьи повернем эту проекциюв плоскостипо часовой стрелке на.

Получим треугольник , в котором по ранее доказанному

.

Так как , то

(3.14)

Заметив, что 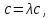 умножим теперь обе части равенства (3.14) на скаляр. Применив свойство 2 векторного произведения, получим:

или ( ), что и требовалось доказать.

Пример 3.12. Показать, что 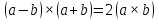, и выяснить геометрический смысл этого равенства. В самом деле:

.

Это равенство означает, что удвоенная площадь параллелограмма, построенного на векторах равна площади параллелограмма, построенного на его диагоналях.

4. Рассмотрим, как векторное произведение векторов

 и  выражается через их координаты:

Так как

пример 3.10), то

. (3.15)

Формулу (3.15) легко запомнить, если воспользоваться определителем третьего порядка. Если формальную конструкцию

расписать по правилам вычисления определителя третьего порядка, то получится правая часть равенства (3.15), поэтому имеет место следующее формальное равенство: