4.3. Основные задачи на прямую на плоскости

Изучим некоторые вопросы, связанные с взаимным положением двух прямых, а также прямой и точек, лежащих в одной плоскости.

Пусть даны две прямые . Углом между этими прямыми, рассматриваемыми в указанном порядке, называется тот угол, на который нужно повернуть прямуючтобы она совпала с прямой(или стала ей параллельна). Знак угла устанавливается по обычному правилу. Так как при добавочном повороте на уголпрямая снова займет начальное положение, то угол между нашими прямыми определяется не однозначно (с точностью до слагаемого, кратного). Одно из значений угла всегда можно выбрать так, чтобы оно было не отрицательным и меньшим. Практически это значение угла обычно и рассматривается.

Пусть прямые заданы соответственно уравнениями

Обозначим 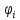 , i=1,2, угол наклона соответствующей прямой к оси абсцисс и черезугол, на который надо повернуть первую прямую до ее совпадения со второй (рис.4.7). Тогдаи

если прямые не являются перпендикулярными.

Заметив, что , получим:

Формула (4.7) определяет тангенс угла, образованного вращением вокруг точки M прямой с угловым коэффициентом 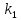до совмещения ее с прямой, угловой коэффициент которой

Если речь идет об угле между двумя прямыми и не указан порядок, в котором они рассматриваются, то можно установить этот порядок произвольно. Очевидно, изменение порядка повлечет изменение знака для тангенса угла.

Если хотя бы одна из данных прямых параллельна оси ординат, то формула (4.7) не имеет смысла. В этом случае, считая, например, что параллельна оси ординат вторая прямая, угол между ними вычислим по формуле:

.

Пример 4.8. Найти угол между прямыми

Перенумеруем прямые в том порядке как они заданы. Тогда угловой коэффициент первой прямой равен 2, а для второй -3. Получаем , откуда

Установим теперь условия параллельности и перпендикулярности двух прямых, лежащих на плоскости.

Прямые параллельны в том и только том случае, если равны тангенсы углов их наклона к оси абсцисс, т. е. когда

. (4.8)

Итак, необходимым и достаточным условием параллельности двух прямых является равенство их угловых коэффициентов.

В случае перпендикулярности прямых (и только в этом случае) можно считать, что . Отсюда следует, что. Или, откуда, или

(4.9)

Таким образом,  необходимым и достаточным условием перпендикулярности двух прямых является равенство -1 произведения угловых коэффициентов этих прямых.

Пример 4.9. Прямые параллельны.

Пример 4.10. При каком значении уравнениеопределяет прямую, перпендикулярную прямой

Построим теперь уравнение прямой, проходящей через заданную точку в направлении, определяемом угловым коэффициентом. Ее уравнение будем искать в виде yлежит на данной прямой, то ее координаты должны удовлетворять этому уравнению, т.е. должно выполняться равенство:

,

Вычитая последнее равенство из уравнения , получим:

. (4.10)

Ясно, что в форме (4.10) можно записать уравнение прямой, не параллельной оси ординат. Если прямая проходит через точку параллельно оси ординат, то ее уравнение будет иметь вид:

.

Совокупность всех прямых, проходящих через некоторую точку называется пучком , а общая их точка - центром пучка.

Если в уравнении (4.10) под понимать величину, принимающую всевозможные числовые значения, то это уравнение будет определять пучок прямых с центром в точке. В форме (4.10) можно записать уравнение любой прямой из рассматриваемого пучка, кроме прямой, параллельной оси ординат.

Пример 4.11. Составить уравнение прямой, проходящей через точку (-3;4) и наклоненной к оси Ox под углом в 135 градусов.

Имеем: ,следовательно, искомое уравнение будет

Пример 4.12. Найти уравнение прямой, проходящей через точку (1;2) параллельно прямой . Угловой коэффициент искомой прямой равен 2/3, а ее уравнение:

Пример 4.13. Найти уравнение прямой, проходящей через точку (-1,1) и перпендикулярной к прямой . Имеем: ее угловой коэффициент равен -1/3, и уравнение:

Пример 4.14. Написать уравнение прямой, проходящей через точку (2;-1) и составляющей угол в с прямой. Угловой коэффициент искомой прямой будем искать, используя формулу (4.7). Задача имеет два решения. Для получения одного из них будем считать5/2,- коэффициент искомой прямой. Имеем:откудаи искомое уравнение суть). Положив=5/2, получим уравнение:.

Пусть на плоскости даны две прямые, заданные уравнениями:

и . (4.11)

Возможны три различных случая их взаимного расположения: прямые пересекаются (то есть имеют одну общую точку), прямые параллельны и не совпадают, прямые совпадают.

Если прямые пересекаются, то координаты точки их пересечения должны удовлетворять обоим уравнениям (4.11). Решая эту систему уравнений, находим, что

Таким образом, если , то прямые пересекаются.

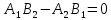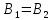Если , то формулы (4.12) не имеют смысла. В этом случае прямые параллельны. Действительно, из условияследует, чтот.е.(если, то прямые параллельны оси Oy и, значит, параллельны между собой). Условиеможно записать в виде 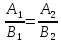0. Итак, если  в уравнениях прямых соответствующие коэффициенты при координатах пропорциональны, то прямые параллельны.

Параллельные прямые в частности могут совпадать. Если , то коэффициенты уравнений при неизвестных и их свободные члены пропорциональны, т.е уравнения (4.15) равносильные. Следовательно, рассматриваемые параллельные прямые совпадают. Если, то параллельные прямые не будут совпадать.

 Необходимым и достаточным условием совпадения двух прямых является пропорциональность соответствующих коэффициентов их уравнений.

Пример 4.15. Найти точку пересечения прямых . Решая совместно эти уравнения, найдем координаты точки пересечения этих прямых:

Пример 4.16. Прямые параллельны, так как

Постоим теперь уравнение прямой, проходящей через две заданные точки.

Пусть на плоскости даны две точки и. Уравнение пучка прямых, проходящих через току, имеет вид:

=, (4.13)

где - параметр. Чтобы выделить из этого пучка прямую, проходящую через точку, потребуем, чтобы координаты этой точки удовлетворяли уравнению (4.13):

. (4.14)

Из равенства (4.14) определим ) и подставим его в (4.13), получим искомое уравнение:

Если данные точки лежат на прямой, параллельной оси абсцисс или оси ординат, то уравнение прямой будет соответственно иметь вид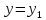или.

Пример 4.17. Найти уравнение прямой, проходящей через точки A(1,2) и B(-1,1). Ответ: .

Пусть теперь даны три точки ,. Уравнение прямой, проходящей через точки, записывается в форме (4.15). Точкалежит на этой прямой в том и только том случае, когда ее координаты удовлетворяют этому уравнению. Тогда необходимым и достаточным условием принадлежности трех точек одной прямой является условие:

Получим теперь  уравнение прямой в нормальной форме.

Пусть на плоскости дана некоторая прямая. Проведем через начало координат прямую перпендикулярно к данной; выберем на ней положительной направление от начала координат в сторону данной прямой (если данная прямая проходит через начало координат, то положительное направление прямойможно выбрать произвольно). Положение данной прямой относительно осей координат можно охарактеризовать, указав ее расстояниеот начала координат и уголмежду осью Ox и осью(рис. 4.8).

Пусть - произвольная точка прямой. Рассмотрим векторы,,и. Так как,то

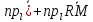+=, (4.17)

но 

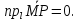
Подставляя найденные значения проекций в равенство (4.17), получим:

или

. (4.18)

Уравнение (4.18) называется  нормальным уравнением прямой.

Заметим, что нормальное уравнение прямой характеризуется двумя особенностями: его свободный член , сумма квадратов коэффициентов при текущих координатах равна единице:

.

Рассмотрим общее уравнение первой степени:

(4.19)

Приведем его к нормальному виду. Для этого обе его части умножим на так, чтобы получилось уравнение вида (4.18). Уравнение (4.19) примет вид:. Положим:

(4.20)

Из равенств (4.20) легко найдем неизвестные ,, p, выраженными через известные коэффициенты. В самом деле:

, или , откуда

В формуле (4.21) нужно брать знак, противоположный знаку свободного члена .

Признак можно выбрать произвольный.

Подставляя найденное значение в формулы (4.20), получим:

Итак, уравнение (4.19) приводится к нормальному виду умножением его на множитель , определяемый по формуле (4.21).

Вычислим теперь расстояние от точки до прямой.

Условимся называть отклонением данной точки от данной прямой число , равное длине перпендикуляра, опущенного из этой точки на прямую, взятой со знаком плюс, если точка и начало координат лежат по разные стороны от данной прямой, и со знаком минус, если они лежат по одну сторону от прямой.

Пусть прямая задана уравнением в нормальной виде

.

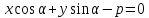Найдем отклонение точкиот этой прямой.

Рассмотрим векторы , ,,, (рис.4.9). Так как

, то как и раньше

и

Отсюда следует, что 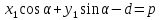, откуда

. (4.22)

Итак,  чтобы получить отклонение точки от данной прямой, нужно в левую часть нормального уравнения этой прямой подставить вместо текущих координат координаты данной точки.

Очевидно, что  расстояние точки от прямой есть абсолютная  величина отклонения и вычисляется по формуле

Пример 4.18. Найти расстояние от точки (-1,1) до прямой . Приводим это уравнение к нормальному виду: умножая его на, получаем:. Отклонение равно. Отрицательный знак дляозначает, что точка лежит с той же стороны от прямой, что и начало координат. Искомое расстояние равно