
- •2010 Г.
- •Глава 1. Элементы математической логики и теории
- •Глава 2. Элементы линейной алгебры
- •Глава 3. Векторная алгебра
- •Глава 4. Аналитическая геометрия на плоскости
- •Глава 5. Аналитическая геометрия в пространстве
- •Глава 1. Элементы математической логики и теории множеств
- •1.1. Аксиоматический метод
- •1.2. Алгебра высказываний
- •1.3. Логика предикатов
- •1.4. Множества и их элементы
- •1.5. Операции над множествами
- •1.6. Отображения множеств
- •1.7. Мощность множества
- •Глава 2. Элементы линейной алгебры
- •2.1. Системы линейных уравнений
- •2.2. Матрицы и действия над ними
- •2.3. Запись систем в матричной форме и их решение
- •2.4. Определители и их свойства
- •2.5. Правило Крамера
- •2.6. Решение системы линейных уравнений снеизвестными методом Гаусса
- •2.7. Теорема Кронекера-Капелли
- •2.8. Обратная матрица
- •2.9. Векторное пространство
- •Глава 3. Векторная алгебра
- •3.1. Система координат на прямой, на плоскости и в пространстве
- •3.2. Векторы и линейные операции над ними
- •3.3. Скалярное произведение векторов
- •3.4. Векторное произведение двух векторов
- •3.5. Смешанное произведение трех векторов
- •Глава 4. Аналитическая геометрия на плоскости
- •4.1. Уравнение линии в заданной системе координат
- •4.2. Различные формы уравнения прямой на плоскости
- •4.3. Основные задачи на прямую на плоскости
- •4.4. Окружность
- •4.5. Эллипс
- •4.6. Гипербола
- •4.7. Парабола
- •4.8. Классификация кривых второго порядка
- •4.9. Построение эллипса, гиперболы, параболы
- •4.10. Кривые второй степени и конические сечения
- •Глава 5. Аналитическая геометрия в пространстве
- •5.1. Поверхности и линии в пространстве
- •5.2. Уравнение плоскости в пространстве
- •5.3. Основные задачи о положении плоскости
- •5.4. Уравнения прямой в пространстве
- •5.5. Основные задачи о положении прямой
- •5.6. Задачи на взаимное расположение прямой и плоскости
- •5.7. Цилиндрические и конические поверхности
- •5.8. Поверхности вращения
- •5.9. Технические приложения геометрических свойств поверхности
4.9. Построение эллипса, гиперболы, параболы
Остановимся
на приемах построения кривых второго
порядка. Начнем с эллипса. Из его
уравнения определяем
 ,
изображая их отрезками
,
изображая их отрезками и
и на осях координат (рис.4.18). Из точки
на осях координат (рис.4.18). Из точки ,
как из центра, радиусом, равным
,
как из центра, радиусом, равным ,
описываем окружность, которая в
пересечении с осью Ox даст фокусы эллипса
,
описываем окружность, которая в
пересечении с осью Ox даст фокусы эллипса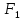 и
и ,
так как при таком построении соблюдается
зависимость
,
так как при таком построении соблюдается
зависимость .
Найдя фокусы эллипса, делим отрезок
.
Найдя фокусы эллипса, делим отрезок на
две части:
на
две части: и
и .
Затем радиусами, равными
.
Затем радиусами, равными и
и ,
описываем две окружности, принимая за
их центры соответственно фокусы
,
описываем две окружности, принимая за
их центры соответственно фокусы и
и .
Точки пересечения этих окружностей
лежат на эллипсе, так как сумма расстояний
каждой из этих точек до фокусов будет
равна
.
Точки пересечения этих окружностей
лежат на эллипсе, так как сумма расстояний
каждой из этих точек до фокусов будет
равна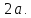 Меняя
Меняя ,
будем получать новые точки эллипса.
,
будем получать новые точки эллипса.

Рис.4.18. Построение эллипса.
Аналогично
проводится построение точек гиперболы.
Определяя из уравнения гиперболы
 изображаем их отрезками
изображаем их отрезками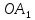 и
и на осях координат (рис.4.19). Из точки
на осях координат (рис.4.19). Из точки ,
как из центра, радиусом, равным
,
как из центра, радиусом, равным , 0
описываем окружность, которая в
пересечении с осью Ox даст фокусы гиперболы
, 0
описываем окружность, которая в
пересечении с осью Ox даст фокусы гиперболы и
и
 (так как при этом построении соблюдается
равенство
(так как при этом построении соблюдается
равенство
 ).
).
Найдя
фокусы гиперболы, описываем из них, как
из центров, две окружности радиусов
 и
и
 .
Точки
.
Точки
 и
и пересечения окружностей лежат на правой
ветви гиперболы, так как разность
расстояний каждой из этих точек до
фокусов будет равна
пересечения окружностей лежат на правой
ветви гиперболы, так как разность
расстояний каждой из этих точек до
фокусов будет равна .
Меняя
.
Меняя ,
будем получать новые точки правой ветви
гиперболы. Изменяя роль фокусов, получим
точки левой ветви гиперболы.
,
будем получать новые точки правой ветви
гиперболы. Изменяя роль фокусов, получим
точки левой ветви гиперболы.

Рис.4.19. Построение гиперболы.
Перейдем,
наконец, к построению точек параболы.
Прежде всего строим фокус и директрису
параболы, откладывая на оси Ox вправо от
 ,
такой же отрезок
,
такой же отрезок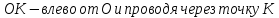 прямую, перпендикулярную к оси параболы
(рис.4.20). Параметр
прямую, перпендикулярную к оси параболы
(рис.4.20). Параметр определяется
из уравнения параболы. Проводим прямую
линию, перпендикулярную к оси параболы,
на произвольном расстоянии
определяется
из уравнения параболы. Проводим прямую
линию, перпендикулярную к оси параболы,
на произвольном расстоянии (
( )
от директрисы и из фокуса
)
от директрисы и из фокуса ,
как из центра, описываем окружность
радиуса
,
как из центра, описываем окружность
радиуса

Рис.4.20. Построение параболы.
Точки
пересечения
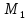 и
и проведенной прямой линии с окружностью
принадлежат параболе, так как для каждой
из этих точек расстояния до фокуса и
директрисы равны между собой.
проведенной прямой линии с окружностью
принадлежат параболе, так как для каждой
из этих точек расстояния до фокуса и
директрисы равны между собой.
4.10. Кривые второй степени и конические сечения
Эллипс, гипербола и парабола могут быть получены сечением прямого кругового конуса плоскостями. Поэтому кривые эти называют 1коническими сечениями.
Под прямым круговым конусом мы понимаем здесь поверхность, которая получается при вращении прямой вокруг некоторой оси, пересекающей эту прямую.
Рассмотрим сечения прямого кругового конуса плоскостями, не проходящими через его вершину (рис.4.21). Можно доказать, что если плоскость пересекает лишь одну полость конуса, не будучи параллельна ни одной из его образующих, то кривая сечения будет эллипсом; если же секущая плоскость будет параллельна одной из образующих конуса, то кривая сечения будет параболой. В том случае, когда плоскость пересекает обе полости конуса, в сечении будет гипербола.

Учитывая
результаты предыдущих параграфах, мы
получаем следующее общее определение
конического сечения (эллипса, гиперболы
и параболы): коническое сечение есть
геометрическое место точек, отношение
расстояний которых до данной точки
(фокуса) и до данной прямой (директрисы)
есть величина постоянная ( ). 0
При этом:
). 0
При этом:
для
эллипса 
для
параболы 
для
гиперболы 
Изученные кривые второго порядка находят весьма широкое применение в военном деле и технике. Прежде всего окружность, комментировать ее роль в нашей жизни думается особой нужды нет, упомянем лишь колесо.
Эллипс и парабола - с их помощью описываются траектории полета космических тел: по окружностям и эллипсам, например, движутся искусственные спутники, если скорость космического аппарата будет равной второй космической, то он покидает сферу притяжения Земли, двигаясь по параболе. По параболе же происходит движение тела, брошенного под углом к горизонту (в отсутствии сопротивления воздуха), в том числе артиллерийского снаряда.
Большую роль в технике играют поверхности, получаемые вращение этих кривых вокруг некоторых осей, но об этом мы поговорим, когда будем рассматривать поверхности второго порядка.
В этой главе мы познакомились с прямыми на плоскости и плоскими кривыми второй степени - окружностью, эллипсом, гиперболой и параболой. Подчеркнем, что этим полностью исчерпывается список линий степени не выше второй, т.е. наш анализ был в этом смысле полным.
