2.2. Матрицы и действия над ними

Прямоугольная таблица чисел

(2.12)

называется матрицей из строк истолбцов. Числа() называютсяэлементами матрицы.  Заметим, что в обозначении элемента матрицы использованы индексыи, указывающие соответственно номер строки и номер столбца матрицы, в которых стоит этот элемент, т.е. индексы указывают место элемента в матрице. Подчеркнем, что первый индекс указывает номер строки, второй - номер столбца. Мы в дальнейшем будем обозначать матрицы заглавными латинскими буквами,,и т.д., а их элементы, по возможности, соответствующими прописными буквами.

Матрица, состоящая из одного столбца, называется матрицей столбцом, состоящая из одной строки - матрицей строкой.

Если матрица состоит из элементови имеетстрок истолбцов, то для описания матрицыбудем часто вместо записи вида (2.12) использовать более компактную запись -.

Количество строк и число столбцовматрицы называются ее размерами. Для указания размеров такой матрицы используется запись(сначала число строк, потом число столбцов).

Рассмотрим матрицу размерами. Ее строку с номером, будем обозначать.  Ее столбец с номером, будем обозначать.

Если число строк матрицы равно числу ее столбцов, т.е. , то матрица называетсяквадратной порядка . Диагональ этой матрицы, идущая от левого верхнего угла до правого нижнего (т.е. состоящая из элементов) называетсяглавной диагональю. Квадратная матрица порядка называетсяединичной матрицей порядка, если все элементы ее главной диагонали равны единице, а все остальные - нулю. Обозначать единичную матрицу порядка будем. Таким образом,

.

Мы использовали матрицы при решении систем двух и трех уравнений, в дальнейшем мы воспользуемся ими для решения систем линейных уравнений общего вида. Но матрицы имеют еще и многочисленные другие применения, которые сделали их предметом большой самостоятельной теории, во многих своих частях выходящей за рамки нашей дисциплины. Сейчас же мы займемся основами этой теории, начинающейся с введения операций над матрицами.

Прежде всего, дадим определения равенства двух матриц. Матрица и матрицаназываютсяравными (обозначается ), еслидля любыхи. Подчеркнем, что речь идет только о матрицах одинакового размера. Таким образом, две матрицы равны, если все их соответствующие элементы равны между собой.

Следующая важная операция над матрицами, которая в дальнейшем еще не раз нам встретится, это транспонирование матриц.

Транспонированием матрицы (2.12) называется такое ее преобразование, при котором ее строки становятся ее столбцами с теми же самыми номерами, т.е. переход к матрице

(2.13)

Матрицу, получающуюся из ее транспонированием, будем обозначать.

Пример 2.4.

Суммой двух матриц иназывается матрица, всякий элемент которой равен сумме соответствующих элементов матрици:

.

Подчеркнем, что операция сложения определяется только для матриц одинакового размера.

Произведением матрицы на числоназывается матрица, получающаяся изумножением всех элементов матрицына.

Пусть ,иматрицы одинакового размера,и- некоторые числа. Введенные нами операции обладают следующими свойствами:

они коммутативны, т.е. и;

они ассоциативны, т.е. и, это свойство позволяет расставлять скобки в произвольном порядке, в том числе, обходится без них; они дистрибутивны, т.е.и .

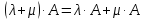Пример 2.5.

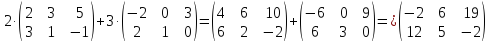
Рассмотрим еще одну операцию над матрицами - их произведение. Можно было бы произведение матриц определить по аналогии с их сложением, перемножая соответствующие элементы. Но такое умножение не находит серьезных применений. Определение произведения матриц, вводимое далее, не смотря на его кажущуюся сложность и непонятность, имеет глубокий смысл и связано с описанием линейных преобразований.

 Произведением  матрицы на матрицуназывается матрица(обозначается, элементкоторой равен сумме произведений соответствующих элементов строкиматрицына столбецматрицы:

(2.14)

Таким образом, чтобы вычислить элемент матрицы произведения, стоящий в i-ой строке и r-ом столбце необходимо взять i-ю строку первого сомножителя и "умножить" ее в соответствии с формулой (2.14) на r-й столбец второго сомножителя.

Отметим некоторые особенности введенной операции.

Умножение определено не для любых матриц, перемножать матрицы можно только если число столбцов матрицы  - первого сомножителя, равно числу строк матрицы - второго сомножителя. 

Уже из этого замечания следует, что произведение матриц не коммутативно, т.е. вообще говоря,  не верно, что .

Число строк матрицы-произведения равно числу строк первого сомножителя, число столбцов - числу столбцов второго.

Произведение матриц ассоциативно, т.е.

?,

при условии, что все указанные здесь произведения определены.

Пример 2.6.

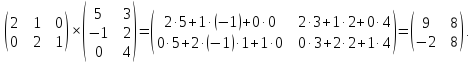
Укажем еще некоторые свойства введенных операций:

Если имеет размеры, тои.

Если матрица квадратная порядка, то, т.е. единичная матрица выступает в роли единицы при умножении чисел, такие аналогии полезно иметь в виду и в дальнейшем.

Пусть матрица является квадратной матрицей порядка. Матрицаразмераминазываетсяобратной  матрице , если

0, (2.15)

т.е. произведение матрицы на обратную (и наоборот) равно единичной матрице.

Конечно, не любая квадратная матрица имеет обратную. На вопросы об условиях существования обратной матрицы и о том, как вычисляются ее элементы мы ответим позже.

Если матрица имеет обратную, то эту обратную матрицу будем обозначать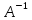0. Здесь опять просматривается аналогия с числами: число обратное числупо умножению естьили.