4.1. Уравнение линии в заданной системе координат

В декартовой системе координат каждой точке плоскости соответствует пара действительных чисел и наоборот. В аналитической геометрии всякую линию рассматривают как геометрическое место точек. В таком определении линии содержится свойство, общее для всех ее точек. Так, окружность с центром в точке O радиусом R есть геометрическое место точек плоскости, расстояние от которых до точки O равно R.

Возьмем на плоскости какую-то линию, выберем в этой плоскости декартову систему координат и рассмотрим произвольную точку этой линии. Если эта точка будет перемещаться по линии, то ее координаты будут меняться, оставаясь связанными некоторым условием, характеризующим точки линии. Таким образом, мы получаем некоторое соотношение между 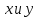, которое будет выполняться только при движении точки по линии и нарушится, если точка сойдет с линии.

Следовательно, линии на плоскости соответствует некоторое уравнение с двумя переменными уравнение между переменными, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней, называетсяуравнением данной линии.  Входящие в это уравнение координаты произвольной точки линии называются текущими координатами.

Пример 4.1. Найти уравнение прямой, делящей отрезок между точками A(1,2) и B(-3,4) пополам и перпендикулярной к нему.

Искомая прямая есть геометрическое место точек, равно удаленных от точек A и B. Следовательно, если точка M(x,y) лежит на этой прямой, то │AM│=│BM│, т.е.

откуда получаем:

.

Пример 4.2. Составить уравнение окружности радиуса R.

Выберем произвольные оси координат. Тогда центр окружности C будет иметь координаты Обозначим черезкоординаты любой точки M рассматриваемой окружности. Расстояний от любой точки M окружности до ее центра C равно радиусу R: │CM│=R. Откуда:

Если начало координат выбрано в центре окружности, то , и уравнение окружности принимает вид:.

Итак, всякая линия, рассматриваемая как геометрическое место точек, определяется уравнением, связывающим координаты ее точек. Вообще говоря, верно и обратное, всякое уравнение между двумя переменными определяет линию как геометрическое место точек, координаты которых ему удовлетворяют.

Рассмотрим уравнение . Пусть при любом значенииэто уравнение, рассматриваемое как уравнение относительно неизвестного, имеет вещественное решение. Положив, найдем соответствующее значение, обозначим егоПара чисел, рассматриваемые как декартовы координаты, определяют в декартовой системе координат на плоскости некоторую точку. Меняямы будем получать разные точки, геометрическим местом которых будет некоторая линия.

 Уравнение определяет линию как геометрическое  место точек плоскости, координаты которых ему удовлетворяют.

Пример 4.3. Построить линию, заданную уравнением

Перепишем это уравнение в виде . Очевидно, что геометрическое место точек, для которых ордината равна абсциссе, есть биссектриса первого и третьего координатных углов. Следовательно, уравнениеопределяет эту биссектрису.

Рассмотрим некоторые особые виды уравнений.

1) Уравнение содержит только одну из текущих координат. Тем не менее оно может определять некоторую линию. Например, уравнение задает прямую параллельную оси Ox, и отстоящую от нее на расстоянии двух единиц. Уравнениезадает прямую, параллельную оси ординат.

2) Левая часть уравнения разлагается на множители. Тогда, приравнивая нулю каждый из них, мы получим несколько уравнений, каждое из которых может определять некоторую линию. Например, уравнениеопределяет пару прямых- биссектрис координатных углов.

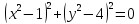3) Уравнение может определять геометрическое место нескольких отдельных точек. Например, уравнениеопределяет единственную точкууравнениезадает четыре точки (1,2), (1,-2), (-1,2), (-1,-2).

4) Может оказаться, что уравнение не определяет никакого геометрического места точек. Так уравнениене имеет вещественных корней.

Если уравнение удовлетворяется лишь в том случае, когда хотя бы одна из переменных имеет мнимое значение, то говорят, что уравнению соответствует мнимое место точек.

В связи со сказанным вытекают две задачи:

дана линия как геометрическое место точек, составить ее уравнение;

дано уравнение, связывающее координаты построить линию, определяемую этим уравнением.

В дальнейшем мы рассмотрим общее решение этих задач в отношении прямой линии. Пока же остановимся на задаче о нахождении точки пересечения двух линий, определяемых уравнениями

.

Если эти линии пересекаются, то точка их пересечения лежит на той и на другой линии. Поэтому ее координаты должны удовлетворять обоим уравнениям и, наоборот, каждая точка, координаты которой удовлетворяют обоим уравнениям, является точкой пересечения рассматриваемых линий. Следовательно, чтобы найти точки пересечения двух данных линий, нужно совместно решить их уравнения. Каждое действительное решение этой системы

уравнений даст точку пересечения. Если же система несовместна или во всех ее решениях хотя бы одно из чисел имеет мнимое значение, то это будет означать, что рассматриваемые линии не пересекаются.

В некоторых случаях при составлении уравнения линии текущие координаты не связывают одним уравнением, а каждую координату в отдельности выражают в виде функции нового переменного . Получают уравнения вида

(4.1)

Эти уравнения составляются так, чтобы значения соответствующие одному и тому же значениюявлялись бы координатами точки, лежащей на данной линии. Уравнения (4.1) называютсяпараметрическими уравнениями линии, а -параметром.  Если в уравнениях (4.1) исключить параметр , то получим уравнение между.

Пример 4.4. Составим параметрические уравнения окружности радиуса R, центр которой лежит в начале координат.

Текущие координаты точки на окружности являются функциями угла , образованного радиусом окружности с осью Ox, проведенным в данную точку. Выразим через него текущие координаты:

Это и есть параметрические уравнения окружности. При желании из них можно получить уравнение окружности в виде, известном из предыдущего. Для этого исключим параметр 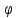. Возводя обе части каждого из уравнений в квадрат и складывая, получим

.

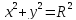Мы рассмотрели уравнения линий в декартовых координатах. Но аналогично можно говорить и о линиях в полярных координатах. Уравнением линии в полярных координатах будем называть такое уравнение между переменными и, которому удовлетворяют полярные координаты любой точки, лежащей на линии, и не удовлетворяют координаты точек, не лежащих на ней.

Пусть, например, требуется найти уравнение окружности, проходящей через полюс, центр C которой лежит на полярной оси, а радиус равен

Соединим отрезками прямой произвольную точку M окружности с полюсом и с конечной точкой D диаметра, проходящего через полюс (рис.4.1). Координатами точки M будут угол и длина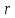отрезка OM. Вспомним, что окружность есть геометрическое место вершин прямых углов, опирающихся на ее диаметр. Следовательно, треугольник OMD - прямоугольный. Отсюда получаем

.

Это и есть искомое уравнение рассматриваемой окружности.

Рис.4.1. Окружность в полярной системе координат.

Заметим, что вид уравнения данной линии зависит от выбора полюса и полярной оси. Так, если мы выберем полюс в центре окружности радиуса то для всех точек этой окружности и только для них полярный радиус будет иметь одно и то же, это равенство и будет уравнением рассматриваемой окружности.

Пользоваться полярными координатами удобно, когда уравнение линии в полярных координатах проще, чем в декартовых.