ми. С помощью t- и F-статистики исследуют линеаризованную модель.

Вопросы для самопроверки

1.Какая модель называется линейной?

2.Какая модель называется нелинейной?

3.Приведите примеры нелинейных моделей, которые являются линейными по параметрам.

4.Какая нелинейная модель называется внутренне линейной?

5.Какая нелинейная модель называется внутренне нелинейной?

6.Что такое ошибка спецификации модели?

7.Перечислите ошибки спецификации и их последствия.

8.Остатки модели имеют некоторую закономерность от номера наблюдения. Что можно сказать о спецификации модели?

9.Какую из двух моделей:

y =α xβ ε, y =α xβ + ε,

можно привести к линейному виду?

10. Является ли полиномиальная модель линейной по параметрам?

ГЛАВА 9. ВРЕМЕННЫЕ РЯДЫ

Цель: изучение моделей тренда, стационарных рядов, нестационарных рядов и динамических моделей.

Методические указания

Внимание следует обратить на составляющие временного ряда. Заметим, что математически модели тренда обычно сводятся к линейным и нелинейным регрессионным моделям, в которых объясняющей переменной является время. Необходимо запомнить, как с помощью коэффициентов автокорреляции и частной автокорреляции распознать вид случайного процесса, и рассмотреть, как оцениваются параметры стационарных временных рядов. Затем рассмотреть расчет разностей различных порядков для приведения ряда к стационарному виду. Наконец, изучить модели с распределенными лагами и авторегрессионные модели.

161

§ 1. Общие понятия

Временной ряд (динамический ряд, ряд динамики) — это со-

вокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени.

В общем виде при исследовании экономического временного ряда yt выделяют следующие составляющие:

•тренд — плавно меняющаяся компонента, описывающая чистое влияние долговременных факторов;

•сезонная компонента — отражающая повторяемость экономических процессов в течение не очень длительного периода (года, месяца, недели);

•циклическая компонента — отражающая повторяемость экономических процессов в течение длительных периодов (например, волны экономической активности Кондратьева, демографические

«ямы»);

•случайная компонента, отражающая влияние не подающихся учету и регистрации случайных факторов.

В общем случае классическая мультипликативная модель временного ряда имеет вид:

yt = trt ×ct × st ×εt ,

(9.1)

классическая аддитивная модель временного ряда имеет вид:

yt = trt + ct + st +εt ,

(9.2)

где yt — значение исследуемой величины, trt — значение тренда, ct — значение циклического компонента, st — значение сезонного компонента, εt — значение случайного компонента, t = 1, 2, …, n — номер периода. Обе модели могут не содержать некоторых из фак-

торов trt, ct, st.

Выбор аддитивной или мультипликативной модели осуществляется на основе анализа структуры колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда. Если амплитуда колебаний приблизительно возрастает или уменьшается, строят мультипликативную модель временного ряда.

162

После изучения графика временного ряда обычно пробуют выделить тренд, сезонные и периодические компоненты. После их исключения временной ряд должен стать стационарным. Кроме того, для облегчения дальнейшего анализа иногда используются преобразования значений ряда; это позволяет приблизить распределение его значений к нормальному или стабилизировать дисперсию этих значений.

§ 2. Моделирование тренда временного ряда

Если циклические и сезонные колебания отсутствуют, то ряд содержит тренд и случайную компоненту.

Важной классической задачей при исследовании экономических временных рядов является выявление и статистическая оценка основной тенденции развития изучаемого процесса.

Одним из наиболее распространенных способов моделирования тенденции временного ряда (тренда) является построение аналитической функции, характеризующей зависимость уровней ряда y от времени t:

yt = f (t, β)+εt ,

(9.3)

где f () — функция тренда (она обычно полагается гладкой),

β — неизвестные параметры модели (их необходимо оценить),

t — время (рассматривается как независимая переменная),

εt — независимые и одинаково распределенные случайные величины (распределение полагается нормальным).

В этом случае переменная времени t замещает собой все другие факторы, от которых может зависеть переменная y. Для построения трендов чаще всего применяются следующие функции:

• линейный тренд f (t, β)= β0 + β1t ;

•гипербола f (t,β)= β0 + β1t ;

•экспоненциальный тренд f (t,β)= β0 eβ1t ;

•тренд в форме степенной функции f (t,β)= β0tβ1 ;

•полином второго и более высоких порядков;

•f (t, β)= β0 + β1t + β2 t2 +... + βm tm .

163

Параметры каждого из перечисленных трендов можно определить обычным методом наименьших квадратов (МНК) (если значения случайного члена не коррелированны), используя в качестве объясняющей переменной время t = 1, 2, …, n, а в качестве зависимой переменной — фактические уровни временного ряда yt. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации. Отказ от взаимной некоррелированности регрессионных остатков повлечет за собой необходимость применения методов устранения автокорреляции.

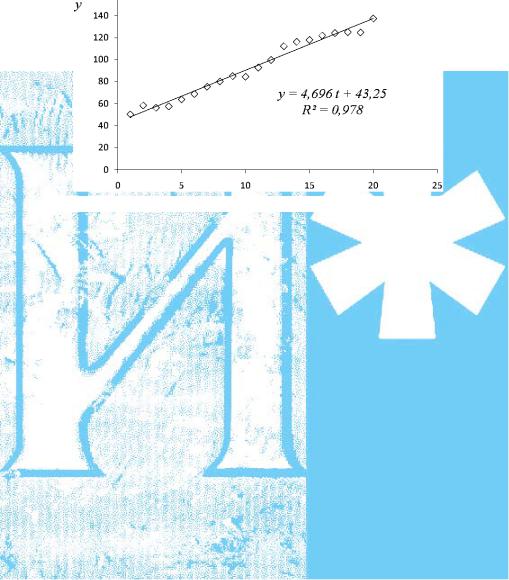
Пример 9.1. Имеются данные (табл. 9.1) о реальном доходе фирмы за ряд лет.

					Таблица 9.1
	Реальный доход фирмы yt (млн. руб.)
Год	t	yt	Год	t	yt
1989	1	50,3	1999	11	92,8
1990	2	58,4	2000	12	99,7
1991	3	56,3	2001	13	112,1
1992	4	57,6	2002	14	116,1
1993	5	63,8	2003	15	117,9
1994	6	68,8	2004	16	121,8
1995	7	75,4	2005	17	124,1
1996	8	80,1	2006	18	124,8
1997	9	85,0	2007	19	124,6
1998	10	84,4	2008	20	137,2

Исходные данные и результат моделирования показаны на рис. 9.1.

164

t

Рис. 9.1. Реальный доход фирмы (линейный тренд)

Проведем аналитическое выравнивание ряда yt с помощью линейного тренда β0 + β1t +εt . Заменив x на t, рассчитаем коэффи-

циенты b0, b1 эмпирического уравнения yˆt =b0 + b1t по формулам для случая парной линейной регрессии:

		n	n	n			n
b0 =		∑yt ×	∑t2 − ∑t × ∑t yt
		t=1	t=1	t=1		t=1		= 43,25,
						2
			n		n
		n ∑t2 − ∑t
			t=1	t=1
		n		n	n
b1 =		n ∑t yt − ∑t ×			∑yt
	t=1			t=1	t=1		= 4,696.
				n	2
		n
		n ∑t2 − ∑t
		t=1		i=1

Врезультатеполучимуравнениелинейноготренда: yˆt = 43,25 + 4,696 t .

В случае линейного тренда yˆt = b0 +b1t интервальный прогноз на глубину τ (на τ шагов вперед по времени) имеет вид:

165

n

−yˆ

2

2

∑(y

)

1

y(n +τ)= b0

+b1

(n +τ)±tα

,n−2 ×

t=1

t

t

×

+ (nn+τ−t)

,

n −2

2

n

∑(t−t)2

t=1

где tα2 , n−2 — критерий Стьюдента.

Произведем интервальный прогноз на 5 лет вперед (n +τ = 20 +

+5 = 25):

y(25(2013годãîä ))= 43,25 + 4,696 ×25 ± 2,101×

		327,07		1		(25 −10,5)2
	×		×		+			=160,7 ± 5,4.
		18		20		665

Сумма квадратов остатков рассчитывается аналогично случаю парной линейной регрессии:

n	n
∑et2	= ∑(yt −yˆt)2 = 327,07.
t=1	t=1

Если уравнение тренда имеет вид полинома:

yˆt = b0 +b1t +b2t2 +... +bm tm ,

где t = 1, 2, …, n, тогда, произведя замены, переходят к модели множественной регрессии. Соответствующие матрицы имеют вид:

y1				1	1	12 ...		1m		b0
						22 ...						= (X T X )−1 X T Y.
Y = y2		,	X =	1	2			2m ,		B = b1
...			... ...			... ...		...		...
y	n			1	n	n	2 ...	n	m	bm

§3. Тренд, сезонные колебания

ификтивные переменные

Рассмотрим модель, которая содержит тренд, сезонную компоненту и случайный фактор. Выбор аддитивной или мультипликативной модели осуществляется на основе анализа структуры колебаний. Если амплитуда колебаний приблизительно постоянна, строят адди-

166

тивную модель временного ряда. Если амплитуда колебаний приблизительно возрастает или уменьшается, строят мультипликативную модель временного ряда. Для анализа сезонной компоненты будем использовать фиктивные (бинарные) переменные.

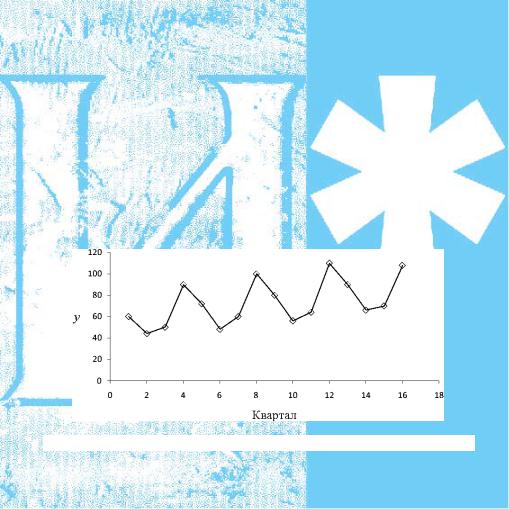
Рассмотрим построение аддитивной модели временного ряда. Пример 9.2. Пусть за несколько лет имеются поквартальные данные об объеме потребления электроэнергии yt, t — номер квар-

тала по порядку.

								Таблица 9.2
		Потребление электроэнергии (тыс. кВт × час.)
	t	yt	t	yt	t	yt	t		yt
	1	60	5	72	9	80	13		90
	2	44	6	48	10	56	14		66
	3	50	7	60	11	64	15		70
	4	90	8	100	12	110	16		108

График (рис. 9.2) свидетельствует о наличии тренда и сезонной компоненты.

Рис. 9.2. Поквартальное потребление электроэнергии Y

Для моделирования сезонных колебаний используем фиктивные переменные. Эмпирическая модель, включающая линейный тренд и сезонные колебания, имеет вид:

yt = b0 + b1t + c1 x1 + c2 x2 + c3 x3 .

167

Качественная переменная (квартал) имеет четыре альтернативы, следовательно, для ее описания необходимо использовать три

бинарных переменных x1, x2 , x3 (табл. 9.3). Имеем модель множественной линейной регрессии с четырьмя объясняющими переменными.

Таблица 9.3

Значения фиктивных переменных

	Квартал года	x1	x2	x3
	1	0	0	0
	2	1	0	0
	3	0	1	0
	4	0	0	1

Имеем модель множественной линейной регрессии, исходные матрицы и оценки параметров имеют вид:

	1	1	0	0	0				60
		2	1	0	0					44
	1
	1	3	0	1	0					50
		4	0	0	1					90
	1
	1	5	0	0	0					72
		6	1	0	0					48
	1																62 ,4
										60
	1	7	0	1	0												1,88
X =	1	8	0	0	1		, Y		100			, B	= (X T X )	−1	X T Y
		9	0	0	0			=		80						= − 23 ,88		.
	1
		10	1	0	0												− 18 ,25
	1								56								20 ,88
		11	0	1	0					64
	1
	1	12	0	0	1				110
		13	0	0	0					90
	1
	1	14	1	0	0					66
		15	0	1	0					70
	1
		16	0	0	1
	1								108

Таким образом, yˆt = 62,4 +1,88 t − 23,88 x1 −18,25 x2 + 20,88 x3 .

168

На графике (рис. 9.3) показан результат моделирования.

Рис. 9.3. Выравненные значения потребления электроэнергии

Рассмотрим построение мультипликативной модели.

Пример 9.3. Пусть за несколько лет имеются поквартальные данные о доходе фирмы (млн. руб.) yt, t — номер квартала по порядку (табл. 9.4).

									Таблица 9.4
				Доход фирмы (млн. руб.)
	t	yt	t		yt	t	yt	t		yt
	1	190	5		230	9	280	13		340
	2	158	6		195	10	230	14		285
	3	150	7		174	11	230	15		260
	4	220	8		310	12	380	16		465

Амплитуда сезонных колебаний (рис. 9.4) растет с течением времени.

Применим для моделирования мультипликативную модель. Эмпирическое уравнение имеет вид (показательная зависимость):

yt = b0 ×b1t ×c1x1 ×c2x2 ×c3x3 ,

где x1, x2 , x3 — бинарные переменные. Прологарифмировав обе части уравнения, получим аддитивную модель:

169

ln yt = lnb0 +t lnb1 + x1ln c1 + x2 ln c2 + x3ln c3, y*t = b0 +b1 t + c1 x1 + c2 x2 + c3 x3.

Рис. 9.4. Доход фирмы

Имеем модель множественной линейной регрессии с четырьмя объясняющими переменными. Оценив параметры, получим:

yˆ*t = 5,176 + 0,0516 t − 0,2323 x1 − 0,3483 x2 + 0,1111 x3.

Произведяпотенцирование, вернемсякисходноймодели(рис. 9.5): yˆt =176,98 ×1,053t ×0,7927 x1×0,7059 x2 ×1,1175 x1

170