17.8 Приплив рідини до горизонтальної свердловини в просторово анізотропному пласті за законом Дарсі

Нафтові і газові родовища в основному приурочені до пористих осадових порід, які характеризуються шаруватою будовою, що пояснюється нерівномірністю в часі та перервністю процесів осадоутворення. Скласти загальний аналітичний розв’язок задачі припливу до горизонтальної свердловини в шарово-неоднорідному пласті практично неможливо, оскільки розмаїтими можуть бути розміщення і розповсюдження по площі коефіцієнтів проникності і товщин окремих шарів, а інформація про це недостатня, особливо про розповсюдження і товщини шарів по площі. Проникність продуктивного розрізу в напрямі, перпендикулярному шаруватості, відрізняється від проникності вздовж залягання шарів. Разом з тим усім гірським породам, окрім сипких, притаманна тріщинуватість. Тріщинуватість підсиплює шарову і зональну неоднорідність колектора, причому тонкошарові проверстки більш тріщинуваті, а величина коефіцієнта тріщинної проникності порід залежить від напряму в просторі. Тут подано оцінку впливу просторової анізотропії пласта за проникністю вздовж трьох координатних осей на величину дебіту горизонтальної свердловини.

Враховуючи напрямленість коефіцієнта проникності, розглядаємо продуктивний пласт анізотропним за проникністю вздовж вертикалі (впоперек шарів) та в горизонтальній площині (вздовж шарів). Припускаючи процес фільтрації усталеним, розв’язуємо рівняння:

(17.168)

де x,y,z– просторові координати анізотропного пласта, які співпадають з головними осями тензора проникності;k_x,k_y,k_z– коефіцієнти проникності пласта вздовж відповідних осейx, y, z;p–тиск.

Припускаємо, що в круговому горизонтальному пласті з радіусом контура живлення R_крозміщено горизонтальну свердловину довжиноюL, радіусомr_сна відстанівід покрівлі пласта, товщина якого становитьh(рис. 17.15).

На поверхнях контура живлення пласта і стінки свердловини задаємо відповідно постійні пластовий p_кі вибійнийp_стиски.

Внаслідок складності задачі та з метою одержання простого розв’язку застосовуємо спочатку метод фрагментів. Усю область фільтрації поділяємо на дві зони: зону плоского руху в горизонтальній площині від колового контура живлення пласта (в круговому пласті) до еквівалентного прямокутника (в просторі – паралелепіпеда) та зону плоского руху у вертикальній площині (всередині паралелепіпеда до свердловини в обмеженому прямокутному пласті).

Оскільки горизонтальну свердловину можна розглядати гідродинамічно рівнозначною досконалій вертикальній тріщині однакової з нею довжини (див. вище), то зону навколо свердловини подаємо прямокутним паралелепіпедом, розміри якого становлять Lі 2lу горизонтальній площині таhу вертикальній площині.

Тоді приходимо до плоскої задачі фільтрації нафти в круговому пласті до прямокутника зі сторонами Lі 2l(див. рис. 17.15,б). Тут уже треба розв’язати рівняння Лапласа за відповідних граничних умов:

(17.169)

Замінюємо на площині такий прямокутник еліпсом (у просторі – паралелепіпед замінюємо еліпсоподібною вертикальною свердловиною). Велику піввісь еліпса беремо рівною a = L / 2, а малу піввісьbвизначаємо з умови рівності площ прямокутника і еліпса:

(17.170)

тобто

(17.171)

Значить, маємо приплив в анізотропному пласті до еліпсоподібної свердловини з півосями a_сіb_с.

Приплив до еліпса є рівнозначним припливу до кругової свердловини, радіус якої дорівнює півсумі півосей еліпса, тобто

(17.172)

Основним методом розв’язку таких крайових задач типу задачі Діріхле - Неймана для анізотропних середовищ є метод ізотропізуючої деформації простору. Відтак застосовуємо метод ізотропізуючої деформації простору, тобто проводимо ізотропізуючу деформацію простору за формулами (див. § 7.2):

(17.173)

де x₁,y₁,z₁– координати ізотропного середовища;с– деяка постійна.

Стосовно до горизонтальної площини знаходимо:

(17.174)

де k_г– коефіцієнт проникності ізотропного середовища в горизонтальній площині (коефіцієнт горизонтальної проникності пласта);_г– коефіцієнт анізотропії пласта за проникністю в горизонтальній площині.

Тоді фільтрацію в горизонтальній площині описуємо рівнянням Лапласа в канонічній формі:

(17.175)

Контур свердловини в допоміжному ізотропному пласті із обчисленого колового перетворюється в еліпс з півосями:

(17.176)

Еліптичну свердловину замінюємо еквівалентною круговою з радіусом

(17.177)

Радіус контура живлення анізотропного пласта становив R_к . Контур живлення як ізобара повинен бути еліпсом. Абсолютні величини півосей цього еліпса визначаємо із співвідношень:

(17.178)

звідки знаходимо півосі

(17.179)

Застосовуємо ізотропізуюче перетворення і знаходимо величину еквівалентного радіуса контура живлення пласта, тобто

(17.180)

Таким чином, ми прийшли до задачі припливу нафти до кругової свердловини радіусом r_с"у круговому ізотропному пласті радіусомR_к'з коефіцієнтом проникностіk_г . Розв’язок рівняння (17.175) за сформульованих умов виражається формулою типу формули Дюпюї:

(17.181)

або

(17.182)

де p₁– перепад тиску між контуром живлення пласта і контуром еквівалентного прямокутника,р₁=р_к–р₀;р₀– тиск на контурі еквівалентного прямокутника (див. рис. 17.15,б);

(17.183)

Із формули (17.182) за  _г= 1 випливає формула дебіту горизонтальної свердловини в ізотропному пласті, коли, наприклад, коефіцієнт горизонтальної проникності дорівнюєk_у .

Якщо у формулі (17.182) взяти l = 0, тобто коли нехтувати шириною (розкриттям) тріщини, то одержимо формулу дебіту досконалої вертикальної тріщини в анізотропному пласті:

(17.184)

з якої за _г = 1 слідує отримана вище формула В.П.Табакова (17.18).

У вертикальній площині маємо плоский фільтраційний потік (потік, що припадає на одиницю довжини свердловини Lу вертикальній площині, яка перпендикулярна до осі свердловини) в обмеженому прямокутному пласті, дві протилежні сторони (покрівля і підошва) якого є непроникними, а на двох інших задано постійний тискp₀(див. рис. 17.15,в). Оскільки ми вибрали, що вісьzспівпадає з однією з головних осей анізотропії проникності, а коефіцієнт проникності в горизонтальній площині вище охарактеризували величиною k_г , то згідно з методом фрагментів у вертикальній площині треба розв’язати рівняння:

(17.185)

Здійснюємо ізотропізуючу деформацію простору за формулами (див. § 7.2):

(17.186)

де с– деяка постійна;x₁,z₁– координати ізотропного середовища.

Із рівнянь (17.186) випливає, що постійна сможе бути вибрана довільно, якщо розв’язок містить тільки відношення лінійних величин.

Визначимо коефіцієнт проникності деформованого ізотропного середовища і постійну с. Для цього розглянемо витрату нафти за законом Дарсі в анізотропному та ізотропному пластах. В анізотропному пласті витрата нафти вздовж осіx, що співпадає з однією із осей анізотропії проникності,

(17.187)

де витрату записано із розрахунку на одиницю товщини пласта.

Аналогічно витрата нафти в ізотропному пласті

(17.188)

де k– коефіцієнт проникності ізотропного пласта.

Зрозуміло, що після здійснення ізотропізуючої деформації простору величини витрат нафти повинні залишатися незмінними, тобто q_ан =q_із . Тоді, прирівнюючи вирази (17.187) і (17.188), маємо:

(17.189)

Здійснюючи перехід до початкових координат за формулами (17.186), одержуємо:

(17.190)

звідки коефіцієнт проникності ізотропного середовища

(17.191)

тобто коефіцієнт проникності дорівнює середньогеометричній величині значин коефіцієнтів горизонтальної і вертикальної проникностей.

З іншої сторони, записуємо швидкість фільтрації вздовж осі xтак:

(17.192)

де m– коефіцієнт пористості;t– час.

Переходимо до нових координат в ізотропному пласті:

(17.193)

(17.194)

звідки знаходимо

(17.195)

або, враховуючи вираз (17.191), маємо:

(17.196)

Тоді вирази (17.186) набувають вигляду:

(17.197)

(17.198)

де – коефіцієнт анізотрпії проникності пласта у вертикальній площині.

З урахуванням виразів (17.197) і (17.198) рівняння (17.185) у нових координатах x₁iz₁набуває вигляду рівняння Лапласа в канонічній формі:

(17.199)

Задача припливу нафти в розглядуваному пласті є симетричною відносно осі z₁. Тоді можна обмежитися розглядом тільки однієї частини, наприклад правої на рис. 17.15,в. Зрозуміло, що загальна питома витрата нафтиqдо свердловини зі сторони обох контурів живлення пласта дорівнює подвоєній питомій витратіq₁зі сторони одного із контурів живлення з тискомp₀, тобтоq = 2q₁. Значить, маємо задачу плоского припливу нафти до горизонтальної свердловини в однорідному напівнескінченному пласті з прямолінійним контуром живлення.

Оскільки свердловина знаходиться між непроникними підошвою та покрівлею пласта і поблизу прямолінійного контура живлення з постійним тиском р₀, то, в подальшому, застосовуємо метод відображення джерел і стоків. Для виконання умови непроникності підошви та покрівлі пласта дзеркально відображаємо нескінченну кількість разів у них дану свердловину (див. § 6.4) і отримуємо нескінченний ланцюжок свердловин (стоків), який складається із двох нескінченних ланцюжків, у кожному з яких інтервали між свердловинами однакові і рівні подвійній товщині пласта 2h, а відповідні свердловини в першому і другому ланцюжках зміщені на відстані 2. Для виконання умови постійного тиску р₀ на контурі живлення пласта дзеркально відображаємо усі ці свердловини (стоки) в цьому контурі живлення та в його продовженнях в обидві сторони до нескінченності (див. § 6.4) і отримуємо ще два (третій і четвертий) нескінченні ланцюжки свердловин (джерел). Відтак застосовуємо метод суперпозиції джерел і стоків (див. § 6.2).

Тоді тиск у довільній точці пласта для першого і третього ланцюжків свердловин (стоків і джерел) згідно з методом суперпозиції описуємо формулою:

_(17.200)

де q – дебіт свердловини, що припадає на одиницю її довжини (для стоків і джерел беремо відповідно +q і –q); r_п1, r_п3 – відстані від вибраної довільної точки пласта відповідно до свердловин (стоків) першого ланцюжка і до свердловин (джерел) третього ланцюжка; – деяка постійна;п – номер стоку і відповідного йому джерела.

Аналогічно записуємо тиск для другого і четвертого ланцюжків свердловин:

(17.201)

а відтак результуючий тиск

(17.202)

або

(17.203)

де r_п2, r_п4 – відстані аналогічно r_п1 і r_п3; – деяка постійна;.

Якщо позначити через +q питому витрату початкового стоку (фізичної свердловини) в точці (х₁₀, z₁₀), причому х₁₀ = 0, z₁₀ = –₁ (див. рис. 17.15), то сукупність його відображень у покрівлі та підошві пласта і в контурі живлення можна записати в декартовій прямокутній системі координат так:

для стоків з витратою +q;

для джерел з витратою –q;

а тоді відстані виражаємо відомою із аналітичної геометрії формулою відстані між двома точками з заданими координатами (аналог формули Піфагора)

(17.204)

де для стоків ідля джерел;для джерел і стоків.

Звідси формула результуючого тиску в декартовій системі координат набуває вигляду:

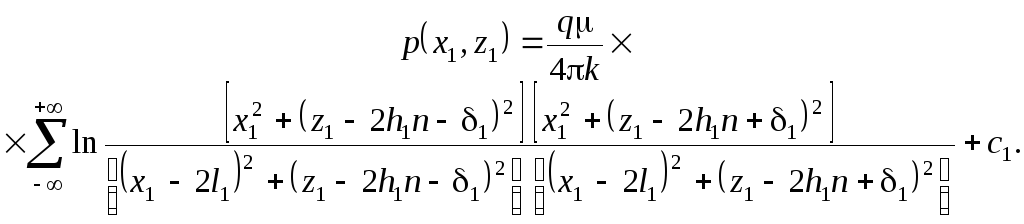_(17.205)

Цей вираз можна спростити, якщо нескінченну суму подати через логарифм нескінченного добутку і використати формули розкладання тригонометричних і гіперболічних функцій через нескінченні добутки. Так, відомо:

(17.206)

де нескінченну константу та інші кінцеві константи відкинуто.

Оскільки в наших позначеннях  = х₁, b = 2l₁,  = z₁  ₁, a = 2h₁, то розв’язок рівняння (17.199) подаємо рівнянням:

_(17.207)

а переходячи до анізотропного пласта, маємо

(17.208)

де p– тиск у довільній точці пласта з координатамиxіz; c₁– деяка постійна.

Вводимо граничні умови:

(17.209)

де r_с– радіус свердловини.

Із другої умови (17.209) знаходимо, що постійна с₁=p₀. Тоді із першої умови одержуємо:

(17.210)

де .

У рівняння (17.210) входить невідома величина l. Для обгрунтування її значини записуємо рівняння (17.208) у вигляді:

(17.211)

що характеризує розподіл тиску в пласті

(17.212)

де – частка загальної депресії тиску, причому= 0 заp =p₀і= 1 заp =p_с;

(17.213)

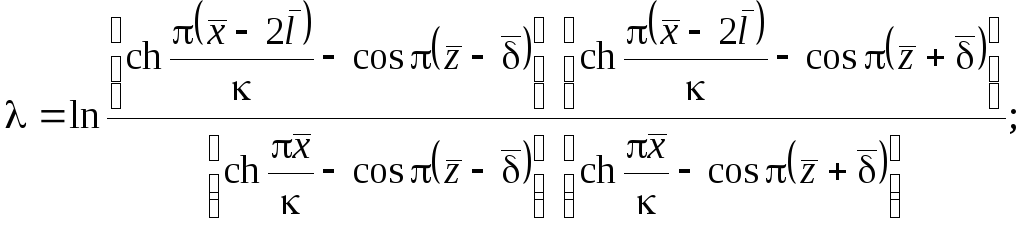(17.214)

За формулою (17.212) виконано розрахунки p, коли2; 5; 10; 50; 100;= 0,1; 0,5; 1,0; 2; 5; 10; 50; 100;0,002; 0,001. На рис. 17.16 представлено приклади розрахунків за= 1; 2; 5.

Із рисунка випливає, що при розв’язуванні задачі для однорідного пласта (= 1) є підстави брати невідому величину(абоl =h), але враховуючи анізотропію проникності, беремо = 2 (абоl = 2h). Цей висновок випливає із того, що з віддаленням від свердловини вздовж осіxрозподіл тиску щораз менше залежить від координати по осіzі заця залежність практично не спостерігається. Чим більша значина коефіцієнта анізотропії проникності пласта, тим ця залежність є відчутнішою.

Приплив нафти до горизонтальної свердловини довжиною L (аналог товщини пласта) у прямокутному, точніше, смугоподібному пласті становить

(17.215)

де p₂=p₀–p_с– перепад тиску між контуром еквівалентного паралелепіпеда (прямокутника) та контуром свердловини;=– коефіцієнт анізотропії пласта за проникністю у вертикальній площині;r_с– радіус свердловини;

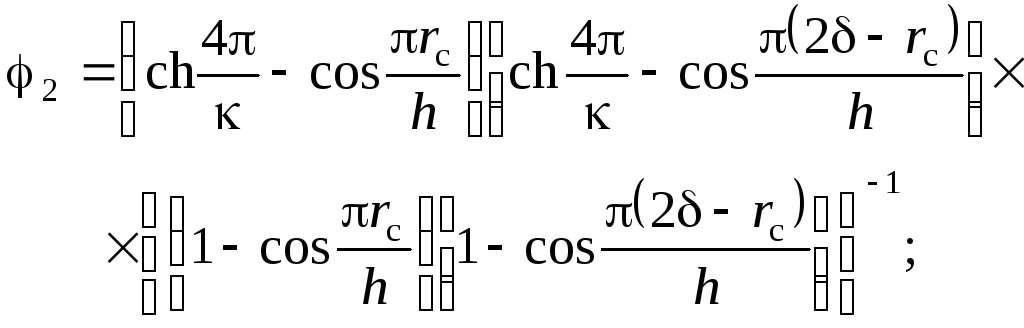_(17.216)

(17.217)

Врахуємо гідродинамічну недосконалість горизонтальної свердловини за характером розкриття пласта (див. § 7.1). Для цього поділимо потік до свердловини в еквівалентному прямокутнику на дві підзони: спочатку до фіктивної досконалої свердловини радіусом R₀ (ділянка плоского потоку у вертикальній площині), а відтак до гідродинамічно недосконалої свердловини за характером розкриття пласта (ділянка стабілізації потоку, за межами якої рух є плоским у вертикальній площині). Відповідно до цих потоків фільтраційні опори можна записати так:

(17.218)

(17.219)

де формулу для ₁ отримано із відповідної попередньої формули заміною r_c на R₀; с₂ – коефіцієнт додаткового фільтраційного опору, який враховує гідродинамічну недосконалість свердловини за характером розкриття пласта (див. § 7.3).

Тоді записуємо загальний фільтраційний опір

(17.220)

або

(17.221)

звідки

(17.222)

де – коефіцієнт додаткового фільтраційного опору рухові рідини до гідродинамічно недосконалої горизонтальної свердловини за характером розкриття пласта;

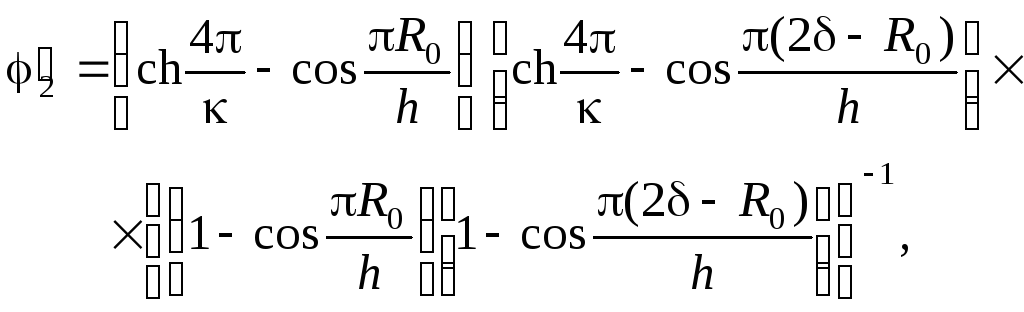_(17.223)

причому ;. Можна брати(див. § 7.4).

Приплив нафти до гідродинамічно недосконалої горизонтальної свердловини в смугоподібному пласті на підставі записаного виражається формулою:

(17.224)

де

Шуканий розв’язок задачі – формулу дебіту горизонтальної свердловини в просторово анізотропному круговому пласті за довільного її розміщення відносно покрівлі (чи підошви) пласта – на основі рівнянь (17.182) і (17.215) за правилом похідних пропорцій внаслідок нерозривності потоку одержуємо у вигляді:

(17.226)

або в разі гідродинамічної недосконалості її за характером розкриття пласта

(17.227)

де p =p₁+p₂ =p_к –p_с– депресія тиску.

Родовище може розбурюватися в сукупності вертикальними і горизонтальними свердловинами. Тоді горизонтальну свердловину доцільно представляти еквівалентною їй вертикальною свердловиною із зведеним радіусом r_с г, тобто

(17.228)

де r_с г=r_с exp (–c_г);c_г– коефіцієнт фільтраційного опору, що зумовлений горизонтальним розміщенням свердловини:

(17.229)

Спростимо формулу (17.224). Аналіз показує, що можна взяти:

(17.230)

(17.231)

(17.232)

Тоді одержуємо першу наближену формулу дебіту горизонтальної свердловини у круговому анізотропному пласті

(17.233)

або

(17.234)

Із (17.234), як частковий випадок, за = 0 з використанням наближення (17.232) одержуємо другу наближену формулу дебіту горизонтальної свердловини без урахування її розміщення відносно покрівлі пласта у вигляді:

(17.235)

Якщо взяти l= 0 і= 1 (k_г=k_в), то стосовно до однорідного пласта із формули (17.235) маємо третю наближену формулу:

(17.236)

Ця формула в третьому наближенні аналогічна формулі Ю.П. Борисова для дебіту горизонтальної свердловини в однорідному круговому пласті, тільки R₀ = r_c, c₂ = 0 ізамість lnh / (2r_с ) маємо lnh / (r_с). Формула Ю.П.Борисова, як і формула (17.236), дає велику розбіжність результатів розрахунку порівняно з формулою (17.226) в анізотропному пласті.

В.Г. Григулецький у формулі Ю.П. Борисова типу (17.236) формально замінив k_гнаk, аh наh, тобто пристосував її до анізотропного пласта. Що стосується останньої заміни, то, як це випливає із формули (17.233), вона є необгрунтованою у виразі під логарифмом, а тому недопустимою.

Нехтуючи в формулі (17.236) внутрішнім фільтраційним опором (другий, третій і четвертий доданки в знаменнику), маємо формулу В.П.Табакова для розрахунку дебіту досконалої вертикальної тріщини в однорідному круговому пласті (див. вище).

Із формул (17.224) і (17.238), опускаючи в знаменнику доданок ln [16R_к _г/(L + 8l)(1 +_г)²], одержуємо відповідно точну і наближену (в першому наближенні) формули дебіту горизонтальної свердловини, яка довільно розміщена відносно покрівлі у смугоподібному анізотропному пласті з двостороннім контуром живлення:

(17.237)

(17.238)

де l– відстань між контурами живлення пласта за симетричного розміщення свердловини між ними.

Нами зіставлено результати розрахунку дебіту горизонтальної свердловини в однорідному ізотропному (_г =  = 1) пласті за нашою формулою (17.215) і точною формулою В.П.Пилатовського (17.148). звідси зроблено висновок, що формула (17.215) порівняно з формулою (17.148) дає розбіжність величини дебіту від – 3 % до + 8 %, коли довжина горизонтальної свердловини зростає від 50 м до 200 м; R_к 750 м; h = 20 м; r_c = 0,1 м;  = h / 2.

Для врахування коефіцієнта анізотропії проникності  у вертикальній площині нами перетворено точну формулу В.П.Пилатовського (17.148) до вигляду:

_(17.239)

де  = а₀ і здійснено заміну L на L / 2 (відповідно до нових позначень).

Числовий аналіз показав, що зі збільшенням коефіцієнта анізотропії проникності  у вертикальній площині, коли коефіцієнт анізотропії проникності у горизонтальній площині _г = 1, дебіти горизонтальної свердловини, розраховані за формулами (17.215) і (17.239), зменшуються (у 1,6 рази за  = 10), а формула (17.215) дає завищення результату порівняно з формулою (17.239) до 8 %, коли  зростає від 1,0 до 10 (решта даних аналогічні попередньому).

Аналіз результатів розрахунків дебіту горизонтальної свердловини за формулою (17.215) показав, що заh= 50 м і= 0,5 hзі збільшенням довжиниLгоризонтальної свердловини до 300-500 м дебітQ зростає, а коефіцієнт фільтраційного опорус_грізко зменшується, при цьому збільшенняLпризводить практично до прямолінійного росту дебітів. В однорідному пласті (= 1) коефіцієнтс_гнабуває від’ємних значин заL> 76 м, колиh= 50 м, а якщо= 10, тос_г < 0 заL >200 м, тобто горизонтальна свердловина стає ефективнішою від вертикальної; для компенсації впливу анізотропії проникності необхідно бурити горизонтальні свердловини із щораз більшою довжиноюL.

Якщо = 20, то горизонтальна свердловина довжиною 500 м стає неефективною (с_г> 0) у порівнянні з вертикальною, заh > 70 м.

Із ростом товщини пласта hдебіт горизонтальної свердловини у круговому пласті збільшується, але за> 10 іh> 100-150 м це збільшення практично відсутнє.

Положення свердловини відносно покрівлі (аналогічно підошви) продуктивного пласта практично не впливає на величину дебіту. Вплив відчутніший за < 0,2h, особливо за великих значин коефіцієнта анізотропії проникності (> 5).

Із ростом _г відношенняQ_ /Q₁інтенсивно збільшується, особливо за великих значинL, де Q_,Q₁– дебіти відповідно за_г 1 і_г = 1.

Збільшення Lтакож призводить до росту відношенняQ_ /Q₁, однак за_г < 5 цей вплив слабко виражений. Дебіт в анізотропному пласті є значно більшим, ніж в ізотропному, коли свердловина перпендикулярна до осі, вздовж якої проникність більша.

Горизонтальна свердловина, якщо ставиться умова одержання найбільшого дебіту, повинна бути розміщена перпендикулярно до горизонтальної осі, вздовж якої проникність є найбільшою. Довжина горизонтальної ділянки стовбура свердловини повинна перевищувати товщину пласта, особливо у високоанізотропних пластах. Застосування одної горизонтальної свердловини (по товщині пласта) є неефективним у товстих (понад 50 м) і високоанізотропних (> 10) пластах.