расчетные методы дозиметрии бета-излучения

частицами, претерпевшими обратное рассеяние от плоской поверхности образца, к энергии частиц, упавших на эту поверхность. Величина Р связана с ξ: P= ξ , где – средняя энергия обратно рассеянных частиц и Е0 – энергия падающих частиц.

Рассмотрим одномерную задачу и пусть плоский источник электронов (“излучающаяплоскость”)расположенвертикальновсреде“I”.Пустьсправаотизлучающей плоскости и параллельно ей расположена плоская граница раздела двухсред,изаней(справойстороны)начинаетсядругаясреда–“2”.Величины альбедо Р1 и Р2 относятся к двум средам. Представим себе, что вместо плоской границы две среды разделяет плоскопараллельная вакуумная щель и пусть в эту щель попадает некоторая «порция” энергии W, движущаяся (с частицами) слева направо, т.е. по направлению к среде “2”. Тогда после первого обратного рассеяниявсреде“2”поглотитсяэнергия,равнаяW(1–P2),аупадётнаповерх- ность среды “I” (двигаясь влево) «порция” энергии WP2 . Эта энергия, в свою очередь, частично поглотится в среде “I” (поглощённая энергия естьWP2(1–P1) ), а частично будет двигаться вправо (эта часть равна WP1P2). Продолжая это рассмотрение дальше, нетрудно прийти к следующему результату: в среде “I”, т.е. слева от границы, поглотится суммарная энергия, равная

WP2(1–P1) (1+P1P2+					+…..)=	–( )			2	1 2
									среде “2” (справа от грани-
цы)	суммарное энергопоглощение						должнов		быть равно W(1–Р )(1+	P P +
			–
P1P2+	+…..)=			.	При этом поглощение энергии (в обеих средах) полу-
чается, как		и должно быть, равным W.

Если мысленно заменить среду “2” справа от границы – такой же, как слева, т.е. “I” (в этом случае граница делает воображаемой), то поглощение энергии в

ней, найденное по формуле – заменой P2→P1 , окажется равным . Из полученных формул нетрудно получить отношение интегральных доз справа

от границы для случаев разных и одинаковых по обе стороны от границ сред:

	( ) (	)	=	( )( – )	(7.17)
( ) ( )				–

Аналогичным способом нетрудно получить отношение энерговыделений в среде“I”(слеваотграницы)ивсреде“2”(справаотграницы)дляслучая,когда плоский источник излучения лежит на границе сред:

( )

(

)=

(– )( )

(7.18

Полученные формулы приближенные, ибо при выводе не учтена возможность изменения величин альбедо с кратностью обратного рассеяния. Кроме того, мы считаем, что величины ξ и Р соответствуют условиям насыщения.

Возможность использования полезных для целей настоящей работы соот- ношений(7.16)–(7.18)определяласьлишьоднимобстоятельством–наличием

160

Сигнальный экземпляр

данных по числовым и энергетическим альбедо электронов для разных значений Е0 и z. Кроме того, были нужны сведения о зависимостях альбедо и от угла падения θ0 электронов на мишень, ибо необходимые величины ξ и Р соответствовали изотропному электронному потоку. Нетрудно показать, что ξип и Рип (для изотропного потока)* могут быть найдены из соотношений:

Рип(z, E0)= (z,E		,θ ) Sinθ cosθ dθ	(7.19)
ξип (z, E0)=		Sin cos d ;

Таким образом, требуемые величины ξ и Р можно было определить по из-

вестным функциям ξ ( z,	) и	).
Сколько–нибудь полной	информации	об указанных функциях в существу-

ющей литературе нет. Несмотря на то, что альбедо для электронов измеряют и вычисляют начиная с 1907 г., т.е. уже более 70 лет, опубликованы только отдельные разрозненные сведения о функциональных зависимостях альбедо от

	и . .
	Для полной оценки функции ξ ( z,	) и	–	) мы воспользовались
новой, никем ранее не использованной возможностью				свойствами геометри-

ческого подобия полей рассеянных электронов для определённых комбинаций значений z и Е0 /56,38/. Эти значения даются семейством непрерывных линий (т.н. “изолиний”) на плоскости с координатными осями z (абсцисса) и E0 (ордината) /38/. На изолиниях выполняются некоторые соотношения между величинами, относящимися к обратному рассеянию электронов, и таким способом удаётся по отдельным, известным из литературы величинам альбедо для нескольких значений z и Е0, найти альбедо и для всех остальных z и Е0, не используя какой–либо дополнительной информации. Методика таких оценок –

применительно к функции ξ ( z,			)	) – изложена в /39/.
Определив функции	ξ ( z,			и		) для нужных нам z, энергий
3 МэВ и диапазона	0≤	≤π/2
					и выполнив интегрирования (8.19), мы

оценили фигурирующие в соотношениях (7.16)–(7.18) величины ξ и Р. Зависимость полученных значений Р от энергии оказалась довольно слабой. Кроме того, характер этой зависимости (медленное уменьшение Р с ростом для всех z) таков, что правые части равенств (7.17) и (7.18) получаются практически одними и теми же для всех энергий. Поэтому нормировки дозных распределений (8.17) и (8.18) зависят фактически только от атомных номеров z граничащих сред. Зависимость числового альбедо ξ от энергии электронов более сильная, чем у Р, и величины νD для разных z (от 7,2 до 48), определяемые по (8.16), варьируют вследствие этого на ±15%. Принятые нами для дальнейших расчётов дозных полей не зависящие от энергии значения νD (z) лежат внутри этих диапазонов вариации.

*) Величины Р, фигурирующие в (7.18), относятся скорее к избранному источнику, однако структура (7.18) такова, что рост всех Р, входящих в ф –му (переход к избр. источнику) почти не изменит отнощения.

161

Исходя из перечисленных выше условий (подгонка под известные дозные распределения в гомогенных и гетерогенных средах, нормировке по дозе и по флюенсу, а также “альбедные” условия), мы пришли к, по–видимому, оптимальной системе параметров, приведённой таблице 7.3.

Таблица 7.3.

Параметры двухгрупового метода расчёта доз от бета–излучения

Параметр									νD				Q
		ν	мг	)			α=				( )
Поглотитель
			–1											1,25
H2O		9 S0				1			0,4	1,1			0,5
Al		11 S–1,01				1,1			0,3	1,1			0,5	1,83
Cu	15 S –1,02					1,3			0,2	1,1			0,5	3,25
	0
Cd	22 S –1,04					1,5			0,145	1,1			0,5	5,17
	0

Величины α и νD в функции z изображены на рис.7.8.

Атомный номер поглотителя

Рис. 7.8 Величины α и νD для различных материалов

Как видно, выбранные величины ν и α отличаются от тех значений, которые были использованы ранее в эмпирической формуле (7.5), описывающей дозные поля в гомогенных средах. Приписав сейчас этой формуле определённый физический смысл, мы вынуждены изменить значения входящих в неё параметров. Необходимость изменения этих значений следует хотя бы из того обстоятельства, что при α=2 и при выражениях для ν, определяемых (7.6), величина Q, вычисляемая из Q=( ν – )/ ( ) получается различной для разных z.

Одним, в рамках принятой двухгрупповой методики расчёта с фиктив-

162

Сигнальный экземпляр

ным источником, соотношения между “направленным” и “диффузионным” флюенсом для сред с разными значениями z. Распределение флюенса от направленного компонента (в случае точечного источника) даётся, согласно

(7.12), формулой					0 ·4πr2=e–ανr , а распределение флюенса от диффузионного
вестно,				νre–νr . Интегралы по объёму от этих величин дадут, как из-
– д (r) 4πr2		=
	суммарные длины электронных треков на стадиях, соответственно, на-
правленного движения и диффузии. Вычисляя, получим отношение:
					4π		4π	=		(7.20)
Величины этого отношенияд						, характеризующие		роль диффузии в процессе

распространения электронов, указаны в последнем столбце таблицы 7.3.

В качестве примера использования формулы (8.13) и данных таблицы 7.3, на рис. 7.9. представлены функции W(r), рассчитанные ЭВМ по Спенсеру и о формуле (7.13), для квадратичного спектра эмиссии с Е0=1900 кэВ для гомогенного кадмия. Расчётом проверено, что для любого поглотителя (H2O,Al, Cu и Cd), ФТИ, вычисленные по данным Спенсера, отличаются от распределений, полученных согласно (7.13) не более чем на ±15% в диапазоне расстояний 0≤r≤S0/2. Напомним, что дозовая функция точечного источника, имеющего реальный спектр эмиссии, получается путём суперпозиции дозных распределений Wi для квадратичных спектров, входящих в разложение исходного. Таким образом, отличие от ФТИ, вычисленных согласно двухгрупповой теории, от расчёта по Спенсеру для различных спектров также не будет превышать ±15%.

W, кэВ мг–1см2

3,0

2,0

1,0

0,5

0,3

0,2

Глубина поглотителя, кадмий

Рис 7.9 ФТИ, рассчитанные по данным Спенсера /сплошная кривая/ и согласно формуле /штриховая кривая/ для квадратического спектра с Еm=1900 кэВ.

163

7.4. Примеры расчётов дозных полей по двухгрупповому методу

7.8.1. Расчёт для гомогенных сред.

Для дальнейших расчётов дозных распределений в различных средах нам понадобятся характеристики некоторых нуклидов, в том числе тех, которые были использованы в эксперименте (147Pm, 204Tl, 32P и 90Sr+90Y). В таблице 8.4. даныпараметрыквадратичныхспектров,суперпозициякоторыхдаётисходный спектр требуемого нуклида. Для получения глубинных дозных распределений в одном из четырёх поглотителей (H2O,Al, Cu и Cd) величины доз от соответствующих квадратичных спектров алгебраически складываются согласно их парциальным весам Pi. Например, требуется вычислить дозу D(a) от источника 32Р в какой – либо точке а пространства, заполненного гомогенными или гетерогенными поглотителями. Источник, в общем случае, имеет произвольную геометрическую форму. Зная дозы в данной точке а от каждого парциального квадратичного спектра в разложении спектра 32P (D1(a), D2(a), D3(a) – здесь индексы 1,2 и 3 обозначают номера парциальных спектров разложения см. табл. 8.4) имеем 32Р:

D(a)=1,47D1(а) –0,5D2(а)–0,03D3(а)

Кроме параметров парциальных спектров, в табл. 8.4 даны также другие величины, используемые для расчёта доз по двухгрупповому методу.

Таблица 7.4 Параметры парциальных спектров некоторых нуклидов и величины,

используемые для расчётов доз по двухгрупповому методу

	Рi	E0 кэВ	кэВ					Поглотитель
							H2O	Al	Cu	Cd
1	2	3	4			5	6	7	8	9
Спектр 1	+2,1	2600	770	90Sr+90Y			1350	1600	1900	2100
				S
					01	мг/см2	0,00666	0,00640	0,0068	0,0077
							2,15	1,80	1,53	1,35
				ν1мг–1см2
				W01 кэВ. мг–1см2
Спектр 2	–1,3	1820	558			S0	900	1080	1300	1430
						ν	0,100	0,0095	0,0100	0,0115
						W0	2,35	1,93	1,65	1,43
Спектр 3	+1,2	650	228			S0	250	310	370	425
						ν	0,0360	0,0335	0,0360	0,0406
						W0	3,4	2,7	2,25	1,90

164

Сигнальный экземпляр

Спектр 1	+0,82	830	770					204Tl		370		440	520	580
						S
							01		мг/см2	0,0243		0,0235	0,0254	0,0294
										3,00		2,43	2,06	1,76
						ν		мг–1см2
							1
					W кэВ. мг–1см2
					01
Спектр 2	+0,13	215	558						S0	50		62	76	90
									ν	0,180		0,170	0,181	0,204
									W0	6,10		4,90	3,90	3,25
Спектр 3	+0,05	70	228						S0	8,0		10,0	12,6	15,0
									ν	1,12		1,07	1,13	1,31
									W0	13,1		10,5	8,20	6,60
Спектр 1	+1,47	1900		580					32P		950	1140	1350	1500
						S01
									мг/см2		0,0095	0,0090	0,0096	0,0109
						ν1мг–1см2					2,32	1,90	1,61	1,41
					W01		кэВ. мг–1см2
Спектр 2	–0,50	1000		326					S0		450	560	650	740
									ν		0,0200	0,0184	0,0202	0,0228
									W0		2,80	2,26	1,91	1,66
Спектр 3	+0,03	330		120					S0		100	125	150	170
									ν		0,0900	0,0838	0,0904	0,1054
									W0		4,60	3,70	3,00	2,60
Спектр 1	+0,58	215		81,7				147Pm			50	62	76	90
						S
									мг/см2		0, 180	0,170	0,181	0,204
						ν01мг–1см2					6,10	4,90	3,90	3,25
					W		1
						01	кэВ. мг–1см2
Спектр 2	+0,24	114		46,1					S0		18	23	28	33
									ν		0,50	0,46	0,50	0,58
									W0		9,40	7,40	5,70	4,80
Спектр 3	+0,15	54		23,5					S0		5,0	6,5	8.2	9,8
									ν		1,80	1,66	1,75	2,05
									W0		16,0	12,7	9,80	8,00
Спектр 4	+0,03	22		10,5					S0		1,00	1,35	1,75	2,20
									ν		9,00	8,12	8,47	9,70
									W0		33,0	25,0	18,2	14,5

Примечания: В таблице 8.4 указаны параметры, относящиеся к квадратичным бета –спектрам; суперпозиция которых представляет собой реальный спектр какого –либо радионуклида (147Pm, 204Tl, 32Pи 90Sr+90Y).

Здесь Pi – парциальный вес квадратичного спектра в разложении исходного спектра; E0 – граничная энергия квадратичного спектра, – его средняя энергия; S0 – максимальный пробег бета– частиц этого кв. спектра в различных поглотителях, ν – коэффициенты поглощения (получены по формулам табл. 8.3); W0 – усреднённые по квадратичному спектру значения тормозных потерь в различных средах (получены по графикам рис. 8.5);

165

						где		– средняя энергия квадра-
=1 (для 90Sr+90Y				=2),	=
тичного	спектра и		– средняя		энергия	спектра	эмиссии данного нуклида.

Плоский тонкий источник Рассмотрим изотропный источник (с квадратичным спектром) в виде бес-

конечно тонкой плоскости, окружённый гомогенным поглотителем. Очевидно, что дозу Dnλ от такого источника, согласно принципу суперпозиции, можно получить интегрированием дозовой ФТИ для точечного источника Ψточ (см. 8.12) по поверхности плоского источника:

		Dnλ ≈		точdS
Здесь – поверхностная	плотность “активности”
			)			/		/.
Выполнив эту операцию, получим:							см
					–х			(7.21)
	Dnλ = W0E1(αx)+ W0( )се
Здесь x=νr , r – расстояние		от источника; константа С равна таковой для

точечного источника С= Q/ νD. Такую же формулу для диффузионного компонента дозы можно получить, решая диффузионное уравнение для плоского тонкого источника.

7.8.2. Расчёты дозных распределений в плоской геометрии для гетерогенных сред.

А. Тонкий широкий источник на границе раздела сред.

Пустьтонкийисточникрасположеннаплоскойграницеразделадвухсопри-

касающихсясред.Выражениедляплотностипотоканаправленногокомпонента
вкаждойизсредбудетиметьтакойжевид,каквслучаегомогенныхпогло-
тителей	. В среде I, характеризуемой параметрами ν1, D1, α1,							/ =		(α1 ν1r)
Аналогично для среды 2:				/ =		(α2 ν2 r)
Решим теперь		диффузионное уравнение (в плоской геометрии) для опре-

деления диффузионного компонента потока. В одномерном случае уравнение

диффузии имеет вид				д” – ν2	д = 0.
Его ограниченные решения						в каждой из сред записываются в виде:
/ = c1	;		/	= c2	(вводим две оси r с началом координат на грани-
це раздела). В	силу непрерывности плотности диффузионного потока на гра-
нице раздела (r=0) имеем:					=	/r=0 ; отсюда c1=c2=cгран/2
Величина константы сгран					находится из условия источника, согласно которо-
му суммарное число диффундирующих частиц, проходящих через единичные

элементарные площадки слева и справа от источника (токи частиц) должно

равняться его мощности, т.е. Q						:
–D1			– D2		= Q (r=0),	что приводит к Q = ν 1D1c1 + ν 2D2c2 или
с1=с2=			= .

Таким образом, полная плотность потока в среде I определится из:

166

				Сигнальный экземпляр
= (α1ν1r) + cгран –
а в среде 2 – из 2 /	=	(α2ν2r)+cгран –
сред получим:
Для доз в каждойΦиз σ			–х
= W01E1 (α1x1)+ W01	(д) cгран
= W02E1 (α2x2)+ W01	(д) cгран		–х		(7.22)

Здесь х1=ν1r; x2=ν2r

Б. Заглубленный тонкий источник

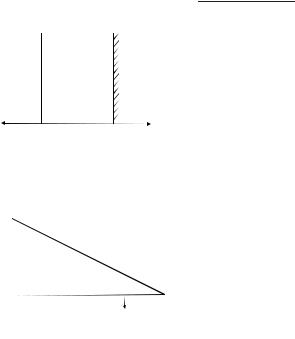
Пусть плоский тонкий источник (бесконечной протяжённости) расположен в среде “I” на расстоянии r0 от плоской границы раздела двух сред (см. рис. 8.10). Отметим, что выражения для направленных компонентов слева и справа от источника в среде “I” имеют такой же вид, как и в случае гомогенного поглотителя.

Вычислим теперь ((плотность потока в среде “2”). Очевидно, что от источника (см. рис. 8.10) в виде малой площадки dS поток нерассеянного компонента в точке а, расположенной в среде “2” за границей раздела будет равен:

dΦ = σ	ᴂ	ᴂ
		( )

1	1	2

r		0			r
						a

Рис. 7.10

Схема к расчёту доз от заглубленного плоского источника

167

Заметим,чтоизподобиятреугольников(см.рис.8.10)следует

=

и

=

.

Где y= y1+y2

и h=h1+h2

В этом случае:

ᴂ1y1+ ᴂ2y2 = y(ᴂ1

+ ᴂ2

) = y (ᴂ1

+ ᴂ2

)= y

где = ᴂ1

+ ᴂ2

Проведя интегрирование

по поверхности источника, получим:

Φ

σ

2

= σ (

h)= σ

σ(ᴂ1 + ᴂ2 )

Или, в других обозначениях, h1=r0

; h2=r–r0

:

=

ᴂ1

+ ᴂ2

)

Решим уравнение диффузии для диффузионного компонента потока и при-

менив условие источника, получим:

Плотность диффузионного потока справа от источника в среде “I” (между

источником и границей)
д (справа) = σ			д	=	σ
Плотность диффузионного потока в среде “2”: “2”:
Здесь – х1=ν1r; х2=ν2r; х01=ν1r0; ; х02=ν2r0

Константы C1 и С2 находим из условий равенства плотностей потоков и токов (–D · δΦ) диффундирующих частиц на границе раздела сред:

C1 =

C2 – = –

Окончательно, получим следующие выражения для доз D в обеих средах: слева от источника, в среде “I” :

2	/σ (лев) = W01E1(α1x1)+W01( )
справа от источника в среде “I”:
2		/σ (прав) = W01E1(α1x1)+W01( )						(7.23)
в среде “2”:
		2D2/ σ = W02E1 [α1x01+α2(x2 – x02)] + W02( )с2
В этих формулах константы определяются из условия						Q=0,5

В. Источник в виде полупространства

Представим себе полупространство с плоской границей, равномерно заполненное бета – излучающими источниками с плотностью “активности”

τ [ мг ]. Между поверхностью источника и границей раздела сред находит-

168

Сигнальный экземпляр

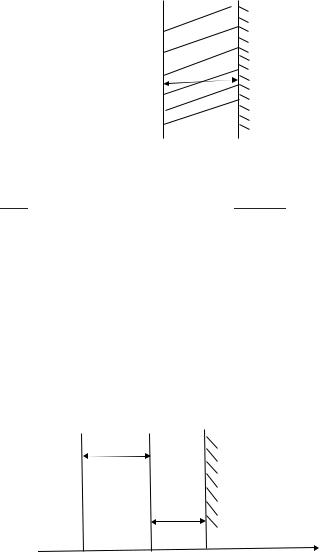
сяблокконечнойтолщиныr0 изтогожематериала,чтоиисточник.Заграницей раздела – среда с другим атомным номером (см. рис. 8.11). Начало координат

– на поверхности источника. Дозу в каждой точке сред I и 2 можно получить интегрированием (8.23) по толщине источника.

среда 1

среда 2

0

Рис. 7. 11

						=W02				[α1x01+α2(x2 – x02)]+ W02( )					(8.24)
где х		=ν		r	; х			=ν	r	; х	=ν	r;Ф– функция Кинга, табулированная, например в
/40/.	01	1		0			02	2	0	2	2	Φ

Г. Источник в виде блока (слоя) конечной толщины

Если источник имеет вид блока конечной толщины h и погружен в полу-

бесконечное пространство, содержащее среду I на расстоянии r0		от границы
раздела сред, то доза в среде “2” определится из очевидного соотношения:
Dблок,2= D2(r01∞) – D2(r0+h1∞)		(7.25)
среда 1
h	граница
	среда 2
	r0

0	r

Рис. 7.12

гдеD2 (r01∞)иD2 (r0+h1∞)–дозыотполубесконечныхисточников,находящихся на расстоянии r0 и r0+h от границы раздела и определяемые по формуле (7.24).

169