§ 5.4. Примеры решения уравнения Шредингера

Пример 1. Свободная частица. Для нее U=0, и уравнение Шредингера имеет вид, знакомый нам по гармоническому осциллятору: . Его решение - гармоническая функция =Аsin(kx+φ₀), где А и φ₀ – постоянные, k =. Учитывая, что 2mE=p², получаем: k=, где λ – длина волны де Бройля (см. формулу 5.1). Таким образом, из уравнения Шредингера следует, что свободная частица – та самая гармоническая волна де Бройля.

Пример 2. Частица в бесконечно глубокой потенциальной яме (БГПЯ).

Потенциальной ямой называется область пространства, где потенциальная энергия достигает минимума. БГПЯ представляет собой бесконечно глубокий колодец с отвесными стенками:

U=  для х<0

U= 0 для х≤0≤а

U=  для х>0

Понятно, что частица может находиться только внутри ямы в области х≤0≤а, где уравнение Шредингера и волновая функция соответствуют свободной частице. Мы рассмотрели ее в примере 1 и получили (х)=Аsin(kx+φ₀). За стенками ямы =0. В соответствии с условиями КОН волновой функции (0)=Аsinφ₀, откуда следует, что φ₀=0, и (а)=Аsinkа=0, а это возможно, когда kа=πn, где n=1,2,3…- любое целое число (n=0 мы использовали на левой границе ямы). Решение уравнения Шредингера дает, что частице в БГПЯ соответствует множество состояний _n (n=1,2 ,…, ) с волновыми функциями _n(х)=Аsin(), являющимися стоячими волнами де Бройля с длинами волн λ_n=2a/n, когда на ширине ямы укладывается целое число половин длин волн. Учитывая, что k=, получаем, что каждому состоянию частицы соответствует своя энергия E_n=. Удовлетворяющие уравнению Шредингера волновые функции и соответствующие им энергии частицы называются собственными функциями и собственными значениями энергии. Совокупность собственных значений энергии образует дискретный ряд. Это значит, что энергия частицы может изменяться не плавно, а ступенчато, т.е. энергия квантуется. Разрешенные значения энергии называют уровнями энергии, номер уровня n называют квантовым числом. Энергия низшего уровня E₁=, энергия всех остальных уровней б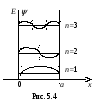ольше наименьшей в n² раз: E_n=E₁n². На рис 5.4 показаны уровни энергии и соответствующие этим состояниям частицы их волновые функции. Найдем различие между соседними уровнями энергии: ∆E=E_n+1 –E_n  n, для n не слишком малых. Пусть электрон находится в потенциальной яме размера атома: а=10^-10 м. Для него ∆EДж 2,5n эВ. Это вполне заметное в опыте квантование энергии. Для маленькой пылинки массой 10 мг в области размером 1 мм ∆E оказывается больше на 34 порядка, т.е. различие между соседними уровнями энергии столь мало, что квантование энергии обнаружить невозможно, так что энергия пылинки, как и всякой классической частицы, может изменяться непрерывно, а не ступенчато. Из рис. 5.4 видно, что плотность вероятности  ² по-разному распределена по ширине потенциальной ямы для частиц с разными энергиями. Так, для n=1 «капкан» для частицы следует установить посередине ямы, тогда как частицу в состоянии n=2 в этом месте ожидать бесполезно. Энергия классической частицы (макрочастицы) соответствует очень большим значениям квантового числа n. Ее волновая функция представляет собой стоячую волну со столь малой длиной волны, что ее узлы и пучности практически сливаются, и плотность вероятности одинакова по всей ширине ямы. Квантовый результат соответствует классическому: частица равномерно движется на любой высоте от одной стенки до другой, изменяя направление скорости на противоположное при упругом столкновении со стенкой. Рассмотренный пример показывает, что уравнение движения квантовой механики органично содержит в себе идеи корпускулярно-волнового дуализма и квантования, и применимо как к микро- , так и макрочастицам.

Пример 3. Туннельный эффект представляет собой проникновение микрочастицы сквозь потенциальный барьер. Потенциальным барьером называется область пространства, где потенциальная энергия U больше полной энергии E, равной сумме кинетической и потенциальной энергий частицы. Согласно классической механики, частица не может оказаться внутри барьера, так как там ее кинетическая энергия должна быть отрицательной, а она по определению не может быть меньше нуля. Налетая на барьер, такая частица должна отразиться от него, и проникнуть за барьер она может лишь в том случае, если в барьере есть туннель. Вспомните железнодорожные туннели, например, в Уральских горах.

П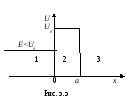ростейший прямоугольный потенциальный барьер представлен на рис. 5.5.

U=0 в области 1, где х<0;

U=U₀ в области 2, где 0≤х≤a;

U=0 в области 3, где х>а.

Решение уравнения Шредингера дает отличные от нуля волновые функции  ₁,  ₂ и  ₃ во всех трех областях: до барьера, внутри него и за барьером.  ₁ и  ₃ – гармонические функции,  ₂ экспоненциально уменьшается с ростом х от 0 до а. Амплитуда волновой функции в области 3 меньше ее амплитуды в области 1, а значит, число частиц N₃~ ₃ ², прошедших сквозь барьер, меньше числа частиц N₁~ ₁ ², падающих на барьер. Прозрачность барьера D характеризует вероятность прохождения частицы сквозь барьер: D= N₃/ N₁~ехр. Заметим, что показатель экспоненты может быть преобразован так: =, где λ-длина волны де Бройля. Если ширина барьера значительно превосходит длину волны де Бройля, то прозрачность барьера практически равна нулю. Туннельный эффект – сугубо квантовое явление, наблюдающееся в микромире. Примером туннельного эффекта является α-распад радиоактивных ядер. Теория туннельного эффекта дает хорошее согласие с измеряемым в опыте периодом полураспада.