§11.4. Сложение взаимно перпендикулярных колебаний

На практике нередко встречаются случаи, когда колебания происходят не в одном направлении. Сначала научимся складывать взаимно перпендикулярные колебания, тогда нетрудно будет складывать два колебания любых других направлений. Действительно, если направление одного колебания взять за опорное, то второе можно разложить на две составляющие, одна из которых параллельна, а другая перпендикулярна опорному колебанию.

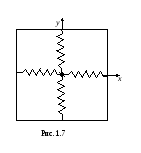
Рассмотрим груз, закрепленный на четырех одинаковых пружинах (рис.1.7), так что одна пара пружин смещает груз вдоль оси x , а другая - вдоль оси y по законам:

x = Asin t

y =B sin( t+)

Начальный момент времени выбран так, что фаза первого колебания равна нулю, тогда

 - разность фаз складываемых колебаний.

Координаты x и y колеблющейся точки задают уравнение ее траектории в параметрическом виде. Исключим параметр t :

sin  t=x/A, cos t=(1 - x²/A²)^1/2,

sin( t+)=y/B

Используем формулу тригонометрии sin(+)=sincos+cossin, подставим в нее предыдущие соотношения и получим уравнение траектории:

x²/A²+y²/B²-2(xy/AB)cos=sin² (1.31)

Из математики известно, что это уравнение эллипса, полуоси которого A и B наклонены соответственно к осям x и y под углом . В частном случае, когда =(2n+1)/2, где n=0,1,2,. полуоси эллипса совпадают с осями координат; и если A=B, эллипс превращается в окружность. Если =2n, или =(2n+1), то эллипс вырождается в отрезок прямой, симметричной относительно начала координат и являющейся диагональю прямоугольника со сторонами 2A и 2B, параллельными соответственно осям x и y . Рассмотрите самостоятельно эти варианты и убедитесь, что в первом случае это диагональ с положительным наклоном к оси х, во втором – с отрицательным.

Если взаимно перпендикулярные колебания имеют разные частоты, то траектория представляет собой сложную линию, вписанную в прямоугольник со сторонами 2A и 2B. Когда отношение частот колебаний _x/_y равно отношению целых чисел, траектория становится замкнутой линией и называется фигурой Лиссажу, форма которой позволяет определить это отношение. Метод фигур Лиссажу используются в измерительной технике.

§ 1.4. Затухающие колебания

Опыт показывает, что свободные колебания реальных физических систем затухают, так как первоначальный запас энергии колебаний расходуется на преодоление сопротивления и превращается в теплоту, излучение и т.д. Количественной характеристикой затухания служит добротность колебательной системы - Q, равная отношению энергии колебаний W к ее потерям W³:

Q=W/W (1.32)

Из определения следует, чем больше добротность, тем медленнее затухают колебания, и тем ближе колебательная система к идеальной. Добротность гармонического осциллятора равна бесконечности.

Рассмотрим свободные колебания пружинного маятника и учтем тормозящее действие на него окружающей среды (например, воздуха). Помимо возвращающей силы F_возвр=-kx действует сила вязкого трения F_тр=-r, где r - постоянный коэффициент, зависящий от размеров и формы тела, а также от вязкости среды,  - скорость тела.. Запишем уравнение движения : md²x/dt²=-kx-r. Учитывая, что =dx/dt, и введя новые обозначения постоянных коэффициентов 2 =r/m и ₀²=k/m. (их физический смысл выясним чуть позже), получаем линейное дифференциальное уравнение второго порядка с постоянными коэффициентами и без правой части:

d²x/dt²+2dx/dt+₀²x=0. (1.33)

Из математики известно, что его решение имеет вид;

x=C₁ exp(₁t)+C₂ exp(₂t), (1.34)

где С₁ и C₂ - постоянные, ₁ и ₂ - корни характеристического уравнения ²+2+₀²=0, равные _1,2=-  .

Проанализируем физический смысл полученного результата. Если силы трения малы, т.е.

 ²-₀² <0, то закон движения (1.34) удобно записать в виде:

x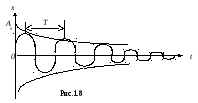=A₀ exp(- t)sin( t+₀), (1.35)

где A₀ и ₀ - постоянные, определяемые начальными условиями, т.е. начальным смещением - x₀ и начальной скоростью - υ₀ при t=0. На рис.1.8 этот закон движения представлен графиком. Это колебание не является гармоническим, так как размах колебаний уменьшается, поэтому понятия “частота”, “период”, “амплитуда” к нему можно применять условно. Промежуток времени между двумя последовательными максимальными отклонениями маятника от положения равновесия в одну и ту же сторону называют периодом колебаний Т. Циклическая частота

 =(₀² -  ²)^1/2 (1.36)

Она тем меньше, а период колебаний T=2/ тем больше, чем больше . Коэффициент перед синусом в законе движения называют амплитудой затухающих колебаний:

A=A₀ e^{-  t} (1.37)

На графике она изображена тонкой линией, огибающей максимальные смещения маятника от положения равновесия. Чем больше коэффициент , т.е чем больше трение, тем быстрее затухают колебания. Коэффициент  называют коэффициентом затухания. Обратите внимание, что  t- есть показатель степени, безразмерная величина, так что коэффициент затухания измеряют в СИ в с^-1. Таким образом, трение тормозит движение колебательной системы, увеличивая период колебаний и уменьшая их размах. В идеальной колебательной системе без трения (=0) частота свободных колебаний =₀ и определяется только свойствами самой колебательной системы (упругостью и массой маятника), поэтому ₀ называется собственной циклической частотой.

В качестве количественной характеристики скорости затухания колебаний используют декремент затухания, равный отношению амплитуд двух следующих друг за другом колебаний: A(t)/A(t+T). Логарифм этого отношения называют логарифмическим декрементом затухания:

=lnA(t)/A(t+T)=T (1.38)

Выясним его физический смысл. Промежуток времени , в течение которого амплитуда уменьшается в е=2,7 раз, называют временем жизни (или временем релаксации) колебаний. Из формулы (1.37) следует, что

=1/ (1.39)

За время  система совершает N_е колебаний. Используя (1.38) и (1.39), получим:

N_e=/T=/=1/ (1.40)

Таким образом, логарифмический декремент затухания равен обратному числу колебаний, уменьшающему амплитуду в е раз. Естественно, что логарифмический декремент затухания связан с добротностью Q:

Q=/=N_e (1.41)

Если силы трения велики (т.е.  ²-₀² 0), то при ₀, как следует из формулы (11.31) ,  ,  . Это означает, что система, будучи выведена из положения равновесия, плавно возвращается к нему. Такой процесс называется апериодическим (т.е. непериодическим). Попробуйте самостоятельно нарисовать два примера апериодических законов движения: мысленно поместите пружинный маятник в очень вязкую среду, отклоните его от положения равновесия и толкните его в первом примере к положению равновесия, а во втором примере в противоположную сторону. Как разные начальные условия отразятся на этих графиках?

Свободные колебания часто встречаются в технике. Если колебания должны поддерживаться длительное время, то затухание вредно и нужно бороться с ним, уменьшая трение. В таких случаях в механических устройствах применяют смазку, подшипники и т.п. Например, в механических часах опоры осей делают конической формы из твердых камней (агат, рубин). Если колебания нежелательны, их стремятся погасить, увеличивая трение с помощью успокоителей (демпферов). Подобные устройства используются в звеньях механических машин, гидравлических устройствах, электроизмерительных приборах.

Нередко к наличию колебаний следует подходить диалектически. Гасить их чрезмерной жесткостью опасно, так как это приводит к ударам, разрушающим здания, перевозимые грузы, станки, стрелки измерительных приборов. Подобные удары амортизируют упругими подвесками, растяжками: сейсмическую стойкость зданий обеспечивают мощной упругой “подушкой“; столы для чувствительных измерений, кузова автомобилей, перевозимые хрупкие предметы крепят на упругих подвесках.

Подведем итоги:

1.Уравнение движения свободных механических колебаний в присутствии сил вязкого трения имеет вид: d²x/dt²+2 dx/dt+₀²x=0, где  - коэффициент затухания,₀ - собственная циклическая частота.

2.Характер закона движения определяется величиной трения. Если трение мало (математически это выражается так:  <<₀), то колебания похожи на гармонические, однако их амплитуда экспоненциально уменьшается со временем; и такие колебания называются затухающими. Быстрота затухания (диссипации энергии) характеризуется логарифмическим декрементом затухания, временем жизни колебаний, добротностью колебательной системы. Эти характеристики взаимосвязаны между собой. Если трение велико ( ₀ ), то движение становится апериодическим.

3.Закономерности свободных колебаний, установленные нами для механического движения, справедливы для колебаний любой физической природы, в частности, для электромагнитных колебаний в электрическом колебательном контуре, имеющем сопротивление.