
- •Занятие 1 Основные элементарные функции
- •Задания для самостоятельного решения
- •Занятие 2 Числовая последовательность. Бесконечно малые и бесконечно большие величины. Предел последовательности
- •Действия над последовательностями
- •Операции над пределами последовательностей
- •Аудиторные задания
- •Домашние задания
- •Занятие 3
- •Предел функции.
- •Раскрытие неопределённостей вида ,
- •Чтобы раскрыть неопределённость, в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от иррациональности.
- •Аудиторные задания
- •Домашние задания Найти пределы:
- •Дополнительные задания
- •Занятие 4 Замечательные пределы
- •Следствия
- •Аудиторное занятие
- •Домашние задания
- •Примерный вариант решения индивидуального домашнего задания «Вычисление пределов»
- •Занятие 5 Вычисление пределов при использовании эквивалентностей
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Занятие 6 Обзорное занятие
- •Занятие 7 Непрерывность функции
- •Аудиторные задания
- •Домашние задания
- •Контрольные вопросы Последовательности и непрерывные функции
- •Функция, её простейшие свойства
- •Вариант 1
- •Литература
- •Содержание
- •Занятие 4
- •Решение идз
- •Занятие 7
Занятие 7 Непрерывность функции
Цели
Знать:
-
Определения: непрерывность функций; непрерывность функции в точке, интервале и на отрезке;
-
основные теоремы о непрерывных функциях и свойства функций, непрерывных на отрезке;
-
классификацию точек разрыва.
Уметь:
-
Определять точки разрыва функции.
▼ Пусть функция y =f (x) определена в точке х0 и в некоторой окрестности этой точки. Функция y =f (x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.
![]() (32). ▲
(32). ▲
▼ Функция y =f (x) называется непрерывной в точке х0, если она определена в точке х0 и её окрестности, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
![]() (33). ▲
(33). ▲
▼ Функция y =f (x) называется непрерывной в точке х0, если её левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т.е.
![]() (34).
▲
(34).
▲
⋙При нахождении предела непрерывной функции f (x) можно перейти к пределу под знаком функции, т.е. в функцию f (x) вместо аргумента х подставить его предельное значение х0:
lim sin x=sin(lim x);
lim arctg x=arctg (lim x); (35)
lim lg x=lg (lim x).
Постановка задачи: Дана функция y =f (x), пользуясь определением непрерывности функции доказать, что функция непрерывна в произвольной точке х0 области определения данной функции.
План решения: Проверить выполнение условий непрерывности функции y =f (x) в точке х0:
-
значение функции в точке х = х0 есть определённое число равное значению f (x0);
-
предел функции y =f (x) при стремлении х к х0 как слева, так и справа, есть одно и то же определённое число
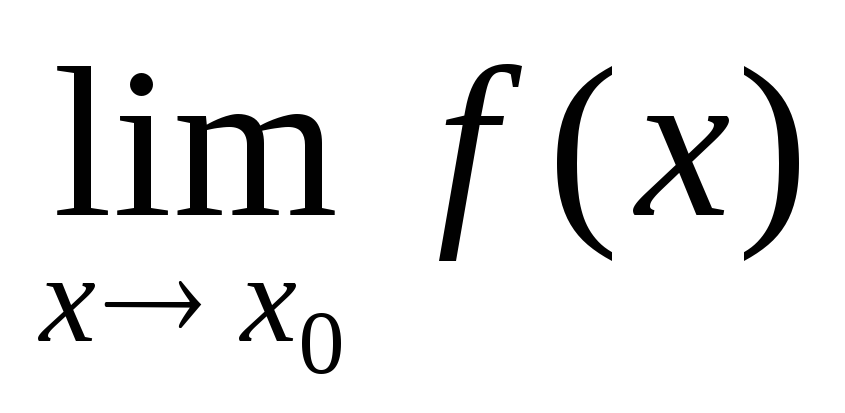 ;
; -
числа
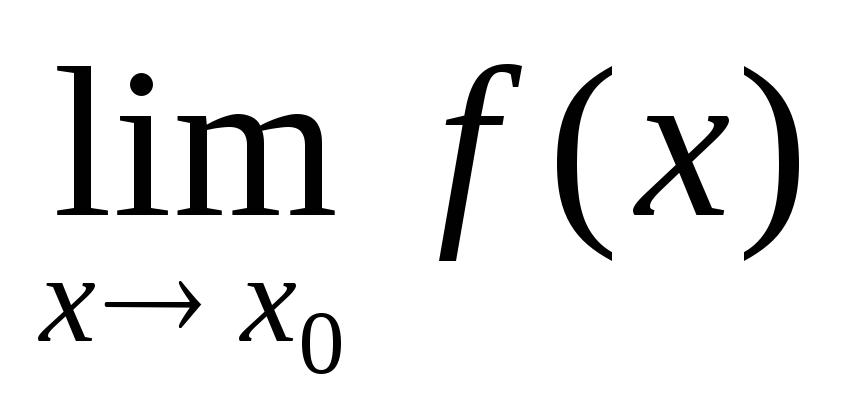 и f (x0)
равны.
и f (x0)
равны.
Если хотя бы одно из условий не выполнено, то функция y = f (x) в точке х0 имеет разрыв.
№16.
Пользуясь определением непрерывности
функции доказать, что функция у=х2
непрерывна в произвольной точке
![]() .
.
Пусть
![]() — приращение аргумента в точке х0.
Найдём соответствующее приращение
функции:
— приращение аргумента в точке х0.
Найдём соответствующее приращение
функции:
![]() =
=![]() =
=
=![]() =
=![]() .
.
Теперь, применяя теоремы о пределе суммы и произведения функций, получим:
![]() =
=![]() =
=
=![]() .
.
Таким образом,
![]() ,
что и означает (по определению)
непрерывность данной функции в точке
,
что и означает (по определению)
непрерывность данной функции в точке
![]() .
◄
.
◄
№17. Доказать, что функция
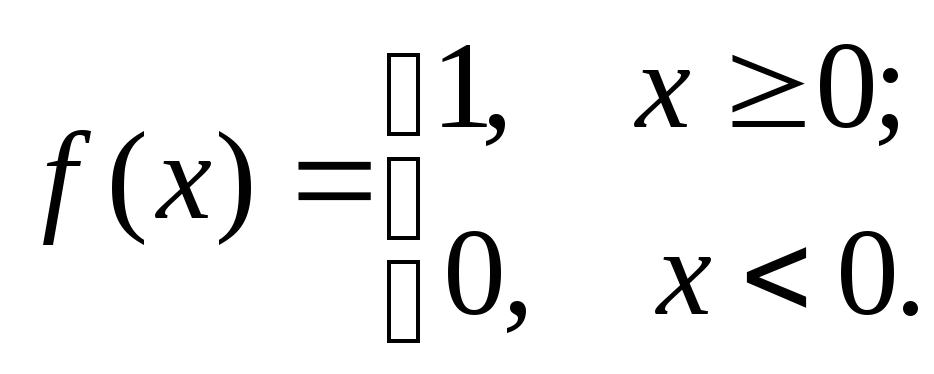
не является непрерывной в точке х0=0, но непрерывна справа в этой точке. Построить график функции f (x).
► Найдём
односторонние пределы в точке х0=0.
Слева от точки х0 имеем f (x)=0,
поэтому
![]() .
Аналогично,
.
Аналогично,
![]() .
.
Кроме того, f (x0) = f (x)=1,
откуда следует, что
![]() .
Это означает, что в точке х0=0
не выполнены все условия непрерывности
функции, но функция f (x)
непрерывна справа в этой точке.
.
Это означает, что в точке х0=0
не выполнены все условия непрерывности
функции, но функция f (x)
непрерывна справа в этой точке.
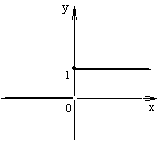
рис.1
График функции изображен на рис.1. ◄
Постановка задачи: Исследовать на непрерывность функцию y = f (x) в точке х0.
План решения:
Найти односторонние пределы функции
y = f (x)
в точке х0, т.е.
![]() и
и
![]() ,
при этом:
,
при этом:
-
если, А1=А2, то точка х0 — точка устранимого разрыва;
-
если
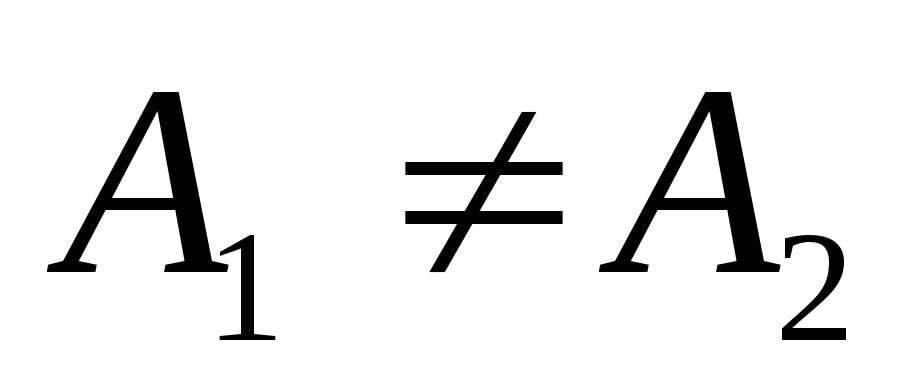 ,
то х0 — точка конечного
разрыва;
,
то х0 — точка конечного
разрыва; -
если, по крайней мере, один из односторонних пределов (слева или справа) не существует или равен бесконечности, то точка х0 — точка разрыва второго рода.
№18. Исследовать на непрерывность функцию
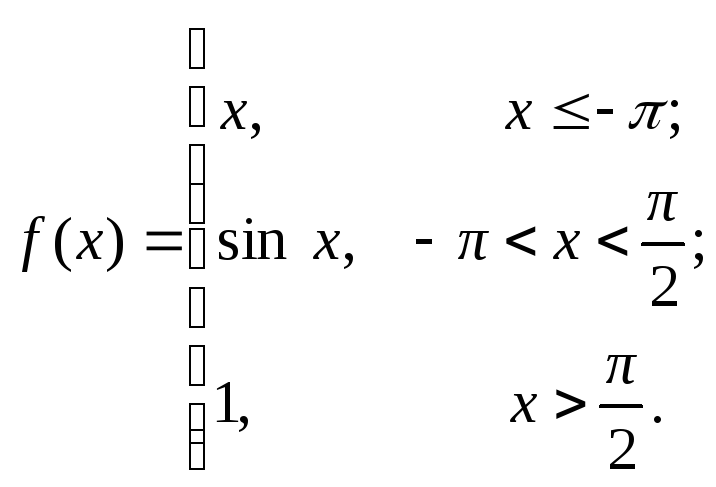
► Функция
у = х, у = sin x
и у =1 непрерывны на всей числовой
прямой, поэтому данная функция может
иметь разрывы только в точках, где
меняется её аналитическое выражение,
т.е. в точках
![]() и
и
![]() .
.
Исследуем функцию на непрерывность в этих точках, для чего найдём соответствующие односторонние пределы и значения функции.
В точке
![]() имеем:
имеем:
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, в точке
![]()
![]() функция имеет разрыв 1-го рода и непрерывна
слева.
функция имеет разрыв 1-го рода и непрерывна
слева.
Скачок функции f (x)
в точке
![]() равен
равен
![]() .
.
Для точки
![]() имеем:
имеем:
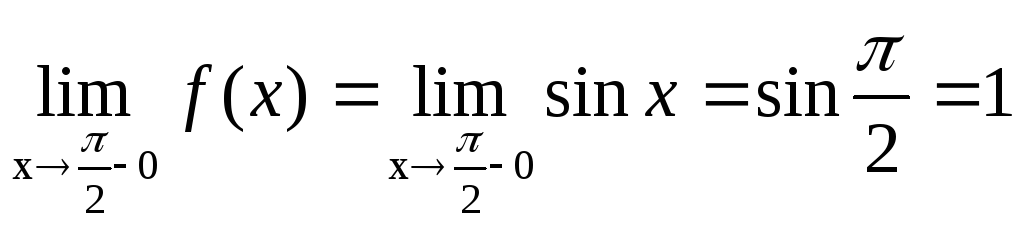 ,
,
![]() ,
,
а значение
![]() не определено. Отсюда следует, что
не определено. Отсюда следует, что
![]() — точка устранимого разрыва. ◄
— точка устранимого разрыва. ◄
№19.
Установить характер разрыва функции
![]() в точке х0=2.
в точке х0=2.
► Находим:
![]() ,
,
![]() ,
т.е. функция в точке х0=2 не
имеет ни одного из односторонних
пределов. Отсюда следует, что х0=2
— точка разрыва 2-го рода. ◄
,
т.е. функция в точке х0=2 не
имеет ни одного из односторонних
пределов. Отсюда следует, что х0=2
— точка разрыва 2-го рода. ◄
