
- •Занятие 1 Основные элементарные функции
- •Задания для самостоятельного решения
- •Занятие 2 Числовая последовательность. Бесконечно малые и бесконечно большие величины. Предел последовательности
- •Действия над последовательностями
- •Операции над пределами последовательностей
- •Аудиторные задания
- •Домашние задания
- •Занятие 3
- •Предел функции.
- •Раскрытие неопределённостей вида ,
- •Чтобы раскрыть неопределённость, в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от иррациональности.
- •Аудиторные задания
- •Домашние задания Найти пределы:
- •Дополнительные задания
- •Занятие 4 Замечательные пределы
- •Следствия
- •Аудиторное занятие
- •Домашние задания
- •Примерный вариант решения индивидуального домашнего задания «Вычисление пределов»
- •Занятие 5 Вычисление пределов при использовании эквивалентностей
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Занятие 6 Обзорное занятие
- •Занятие 7 Непрерывность функции
- •Аудиторные задания
- •Домашние задания
- •Контрольные вопросы Последовательности и непрерывные функции
- •Функция, её простейшие свойства
- •Вариант 1
- •Литература
- •Содержание
- •Занятие 4
- •Решение идз
- •Занятие 7
Аудиторные задания
№9. Написать
первые пять членов последовательности
{xn},
если
![]() .
.
№10. Зная
несколько первых членов последовательности
{xn},
написать формулу её общего члена:
1, ![]() ,
, ![]() ,
, ![]() , …
Определить какие из последовательностей
{xn}
ограничены:
, …
Определить какие из последовательностей
{xn}
ограничены:
№11.
![]() .
Ответ: неограниченная.
.
Ответ: неограниченная.
№12. xn= –ln n; Ответ: ограничена сверху.
Какие из последовательностей монотонные, а какие — строго монотонные:
№13.
![]() .
Ответ:
убывающая.
.
Ответ:
убывающая.
№14.
![]() .
Ответ: неубывающая.
.
Ответ: неубывающая.
№15. Используя
определение, доказать, что последовательность
бесконечно малая
![]() .
.
№16.
Используя определение предела, доказать,
что последовательность
![]() сходится к числу 1.
сходится к числу 1.
Написать первые пять членов последовательности {xn}, если:
№17. xn=![]() .
.
№18. xn=![]() .
.
Зная несколько первых членов последовательности {xn}, написать формулу её общего члена:
№19.
![]()
№20.
![]()
№21. –1, 2, –3, 4, –5, …
Какие из последовательностей {xn} ограничены:
№22. xn=n3+2n. Ответ: ограничена снизу.
№23.
![]() .
Ответ: ограниченная.
.
Ответ: ограниченная.
Какие из последовательностей монотонные, а какие — строго монотонные:
№24.
![]() .
.
Ответ: строго возрастающая, ограниченная.
№25.
![]() .
.
Ответ: строго убывающая, ограниченная сверху.
№26. Пусть
{xn}={n},
![]() — две последовательности.
— две последовательности.
Найти
последовательности {xn+yn},
{xn – yn},
![]() ,
,
![]() .
.
№27. Доказать,
что данная последовательность бесконечно
малая: xn=![]() .
.
№28. Доказать, что данная последовательность бесконечно большая: xn=n2.
№29. Пользуясь
определением последовательности
доказать, что
![]() .
.
Домашние задания
Найти первые четыре члена последовательности {xn}, если:
№30.
![]() .
.
№31. xn=1.
№32.
![]() .
.
№33. x1=2, xn=|xn – 1 – 2|.
№34. xn=n!,
где
![]() .
.
Зная несколько первых членов последовательности {xn}, написать формулу его общего члена:
№35. 2, 5, 10, 17, 26, …
№36. –1, 1, –1, 1, –1, …
№37.
![]()
№38.
![]()
Какие из последовательностей {xn} ограничены, если:
№39. xn=sin x. Ответ: ограниченная.
№40.
![]() .
Ответ: ограниченная
сверху.
.
Ответ: ограниченная
сверху.
№41.
![]() .
Ответ: ограниченная
снизу.
.
Ответ: ограниченная
снизу.
№42.
![]() .
Ответ: неограниченная.
.
Ответ: неограниченная.
Найти
последовательности
![]() и
и
![]() ,
если:
,
если:
№43. xn=n, yn=1;
№44. xn=n2, yn=n.
Доказать, что данная последовательность бесконечно малая:
№45. xn=![]() .
.
№46. xn=![]() .
.
Доказать, что данная последовательность бесконечно большая:
№47. xn=![]() .
.
№48. xn=2n.
Пользуясь определением последовательности доказать:
№49.
![]() .
.
№50.
![]() .
.
Занятие 3
Предел функции.
Раскрытие неопределённостей вида ,
Цели
Знать:
-
Определение предела;
-
признаки существования пределов;
-
основные теоремы о пределах.
Уметь:
-
Применять основные теоремы о пределах;
-
применять признаки существования пределов при вычислении предела функции;
-
вычислять пределы, раскрывая неопределённости вида
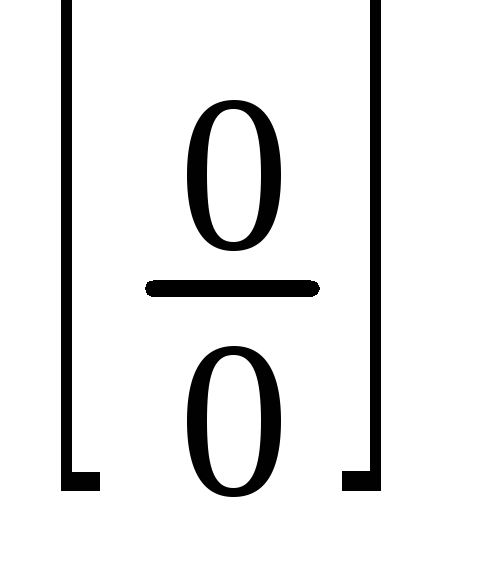 ,
,
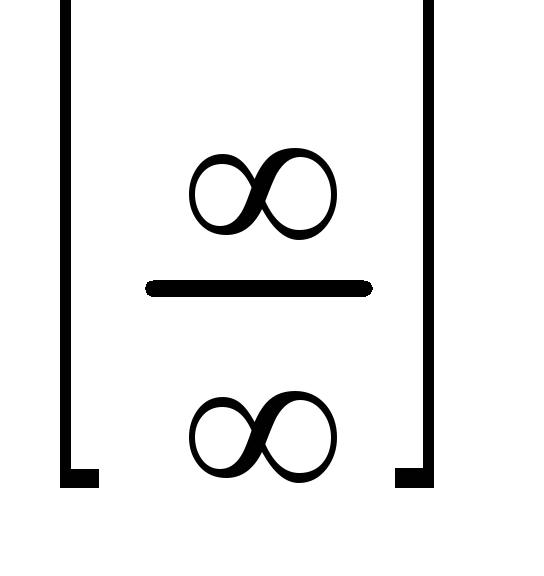 .
.
Определение («на языке последовательностей», или по Гейне)
Число А называется
пределом функции y=f(x)
в точке х0 (или при
![]() ),
если для любой последовательности
допустимых значений аргумента xn,
),
если для любой последовательности
допустимых значений аргумента xn,
![]() ,
сходящейся к х0 (т.е.
,
сходящейся к х0 (т.е.
![]() ),
последовательность соответствующих
значений функции f(xn),
),
последовательность соответствующих
значений функции f(xn),
![]() сходится к числу А (т.е.
сходится к числу А (т.е.
![]() ).
).
Определение (на «языке ε-δ», или по Коши»)
Число А называется
пределом функции y=f(x)
в точке х0 (или при
![]() ,
т.е.
,
т.е.
![]() ),
если для любого положительно ε найдётся
такое положительное число δ, что при
всех
),
если для любого положительно ε найдётся
такое положительное число δ, что при
всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
Основные теоремы о пределах
Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
![]() (22).
(22).
Следствие. Функция
может иметь только один предел при
![]() .
.
Теорема 2. Предел произведения двух функций равен произведению их пределов:
![]() (23).
(23).
Теоремы 1 и 2 справедливы для любого конечного числа функций.
Следствие. Постоянный множитель можно выносить за знак предела:
![]() (24).
(24).
Следствие. Предел степени с натуральным показателем равен той же степени предела:
![]() (25).
(25).
Следствие.
![]() (26).
(26).
Теорема. Предел дроби равен пределу числителя, делённому на предел знаменателя, если предел знаменателя не равен нулю:
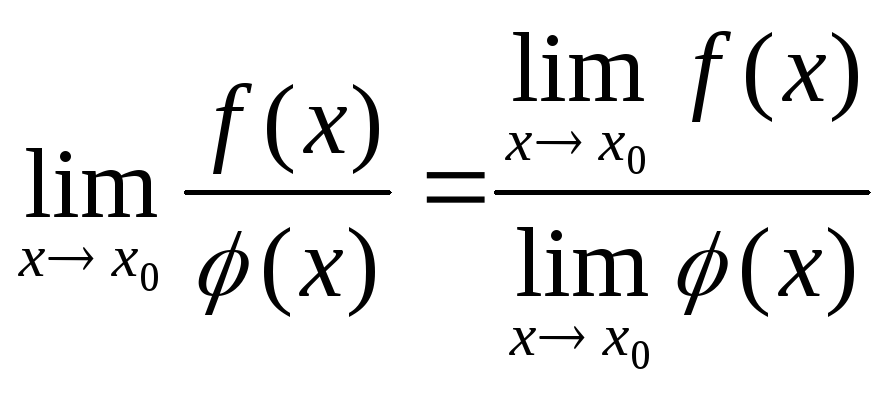 ,
(
,
(![]() ) (27).
) (27).
При нахождении пределов применяют соотношения:
![]() ,
(k=const);
,
(k=const); ![]() ;
;
![]() ;
; ![]() ;
;
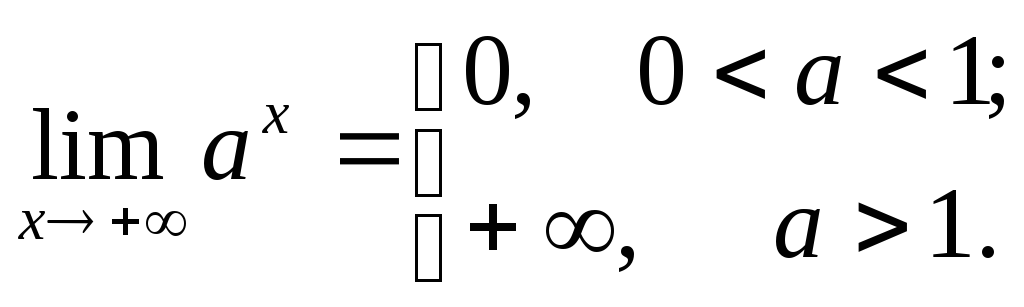 ;
; 
 ;
; 
(28).
Постановка
задачи. Найти
![]() .
.
План решения.
Для того чтобы найти
![]() вычисляем f (х0),
при этом:
вычисляем f (х0),
при этом:
-
если данное выражение имеет смысл, то предел равен этому выражению;
-
если в результате вычислений нет неопределённостей, воспользуемся одним из соотношений (28).
№9. Найти
пределы: 1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() .
.
► 1) Применяя теоремы о пределах, получаем:
![]() =
=![]() =
=
=![]() ;
;
2) Пределы
числителя и знаменателя существуют и
предел знаменателя не равен нулю.
Пользуясь теоремой о пределе частного,
находим:
![]() =
=![]() ;
;
3) Непосредственно
применять теорему о пределе частного
нельзя, так как предел знаменателя равен
нулю (в знаменателе есть бесконечно
малая величина при
![]() ).
В числителе имеем ограниченную величину,
отличную от нуля. Таким образом, под
знаком предела будет произведение
ограниченной величины
).
В числителе имеем ограниченную величину,
отличную от нуля. Таким образом, под
знаком предела будет произведение
ограниченной величины
![]() ,
отличной от нуля, на бесконечно большую
величину
,
отличной от нуля, на бесконечно большую
величину
![]() при
при
![]() как величину, обратную бесконечно малой.
Поэтому
как величину, обратную бесконечно малой.
Поэтому
![]() . ◄
. ◄
Постановка
задачи. Найти
![]() ,
где
,
где
![]() или
или
![]() .
.
План решения.
Для того чтобы найти
![]() вычисляем f (х0),
если в результате вычислений получилась
неопределённость
вычисляем f (х0),
если в результате вычислений получилась
неопределённость
![]() или
или
![]() ,
следует применить соответствующие
правила для раскрытия данных
неопределённостей.
,
следует применить соответствующие
правила для раскрытия данных
неопределённостей.
Неопределённость вида
![]()
