Примерный вариант решения индивидуального домашнего задания «Вычисление пределов»
Найти пределы:
№1.
.
►
=
=
=
.
◄
№2.
.
►
.◄
№3.
.
►
=
=
.
◄
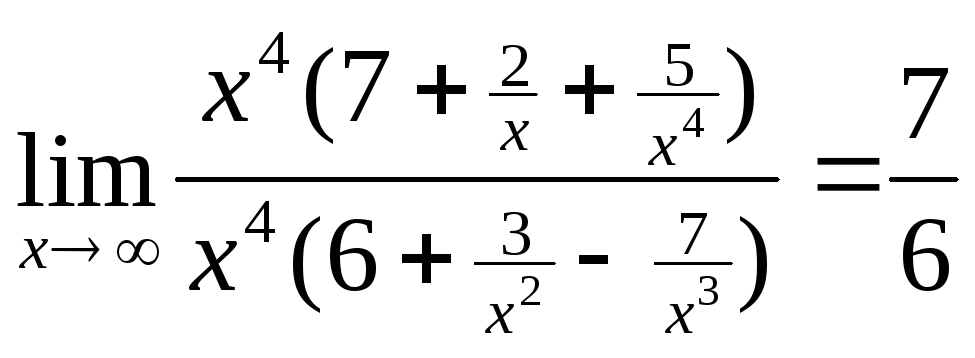№4.
.
►
=
=
=
=
=
.
◄
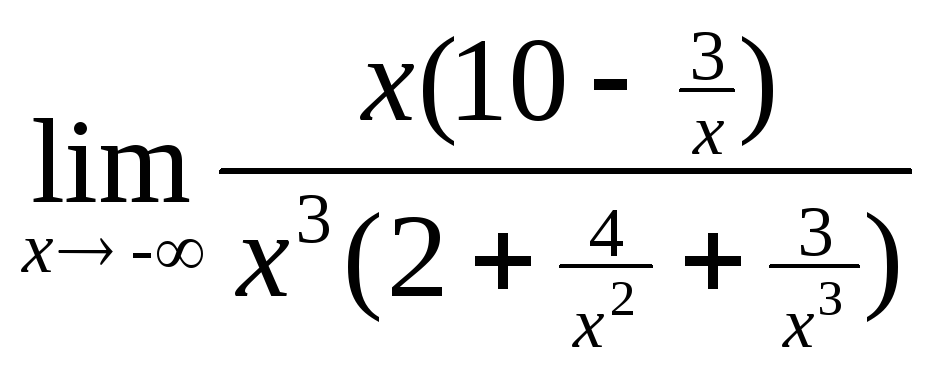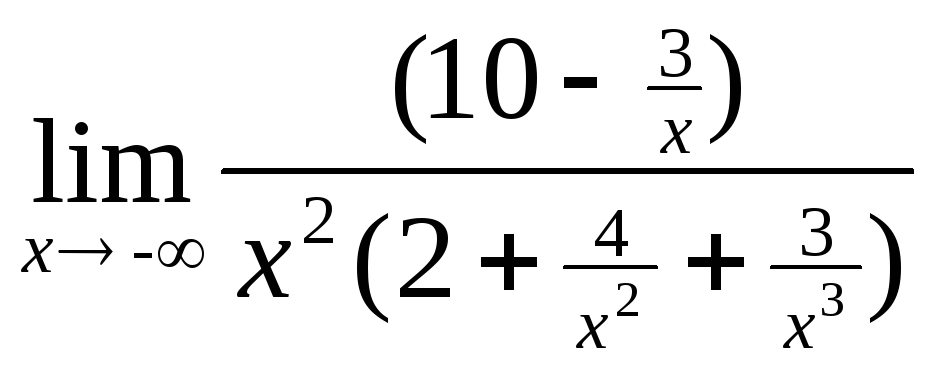№5.
.
►
=
=
=
=
.
◄
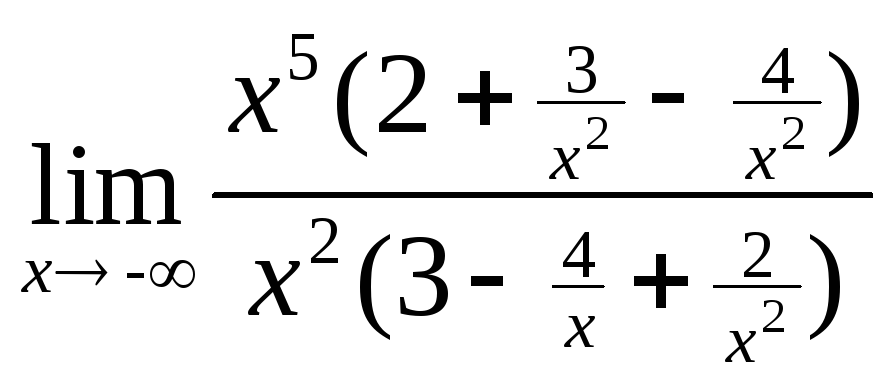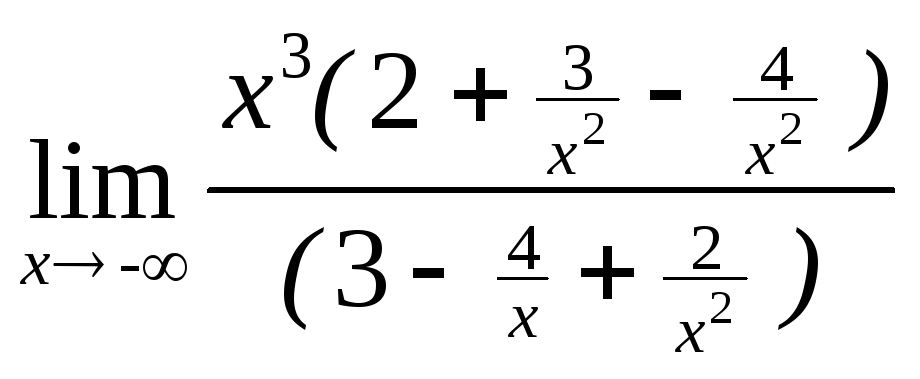
№6.
.
►
=
=
=
=
=
=
=
.
◄
№7.
.
►
=
=
=
=
=
=
=
=
=
=
=
.
◄
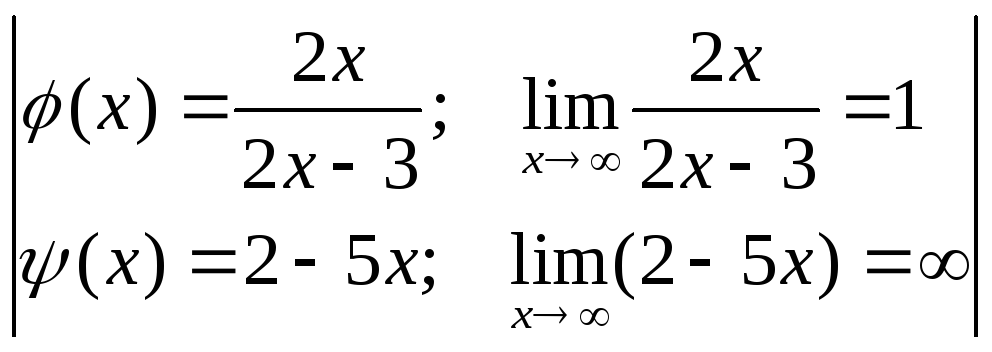№8.
.
►
=
=
=
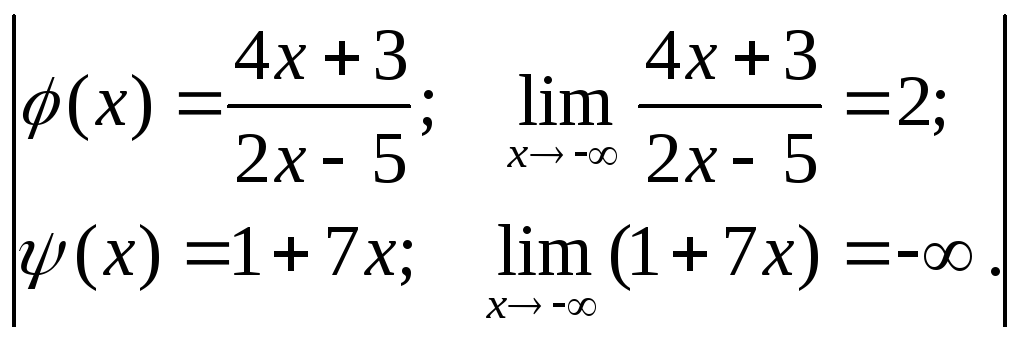=0.
◄
№9.
.
►
=
=
=
=
=
=
=
.
◄
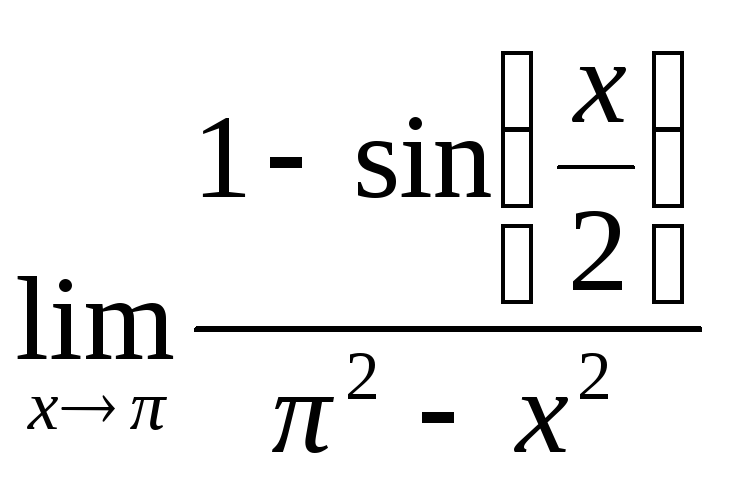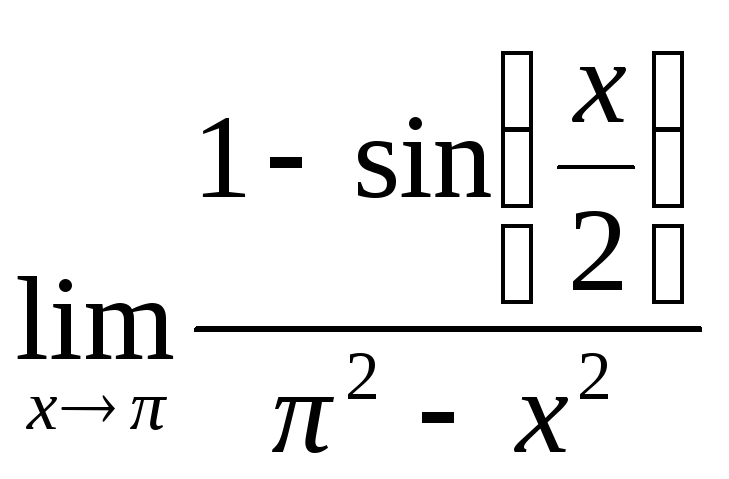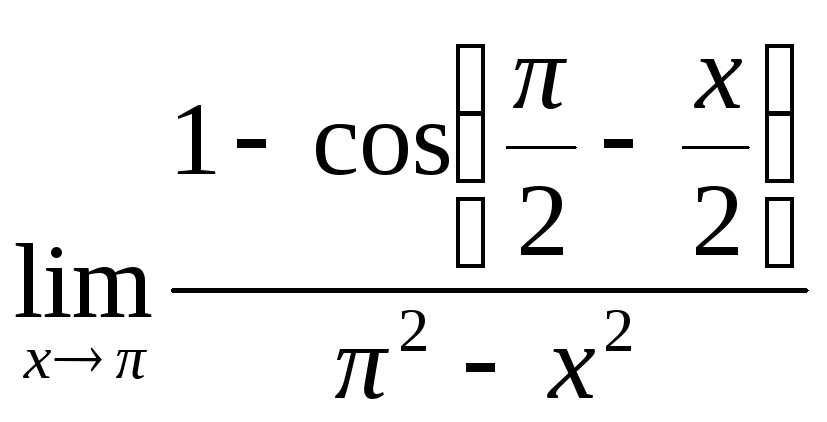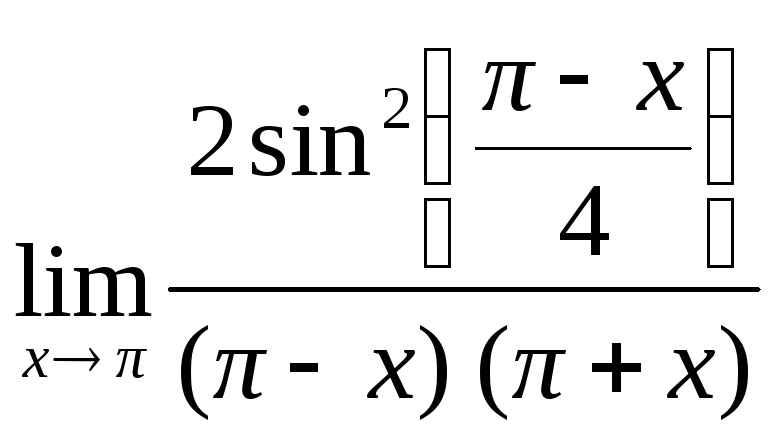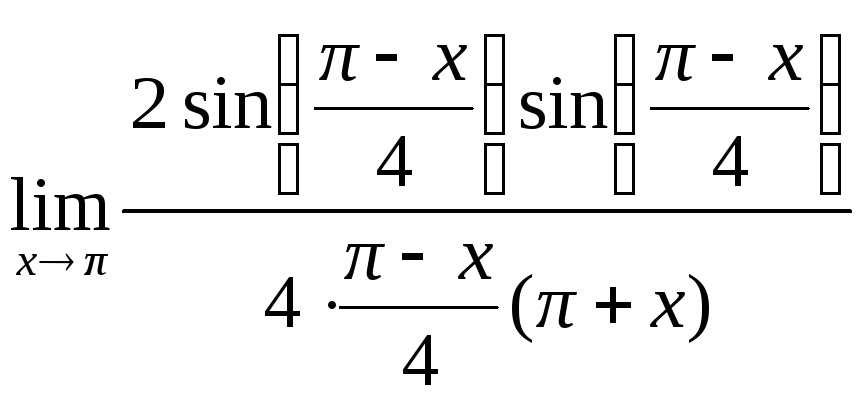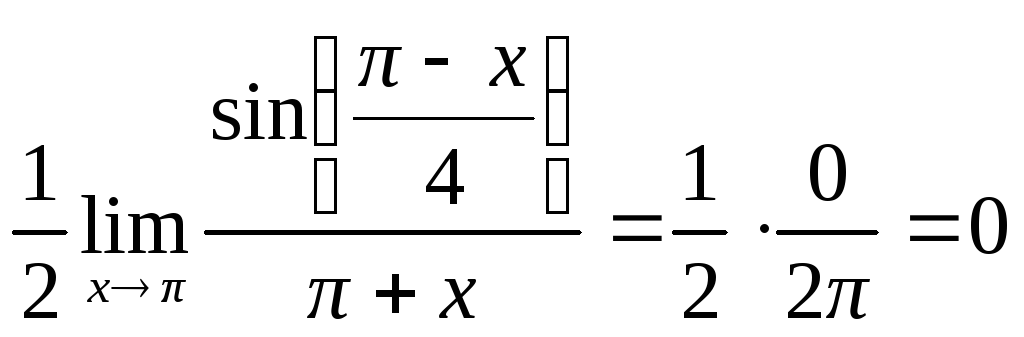Занятие 5 Вычисление пределов при использовании эквивалентностей
Цели
Знать:
-
Эквивалентные бесконечно малые функции и основные теоремы о них.
Уметь:
-
Вычислять пределы, используя основные теоремы эквивалентности.
▼ Если
,
то α и β называются эквивалентными
бесконечно малыми (при
),
это обозначается: α~β. ▲
Важнейшие эквивалентности (31)
-
sin x~x при
; -
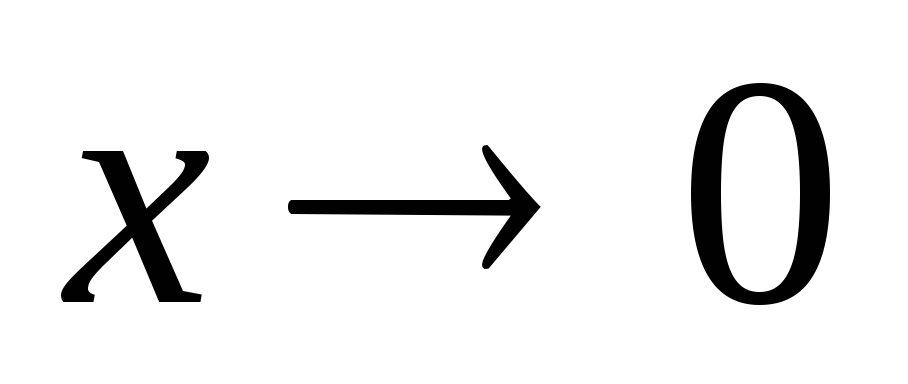tg x~x при
; -
arcsin x~x при
; -
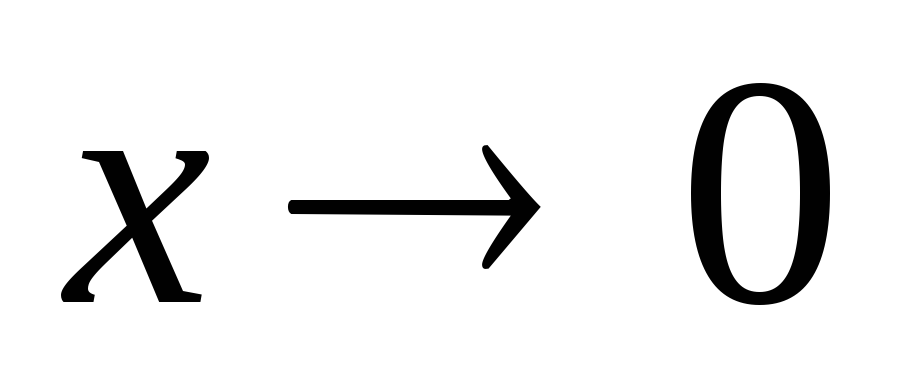arctg x~x при
; -
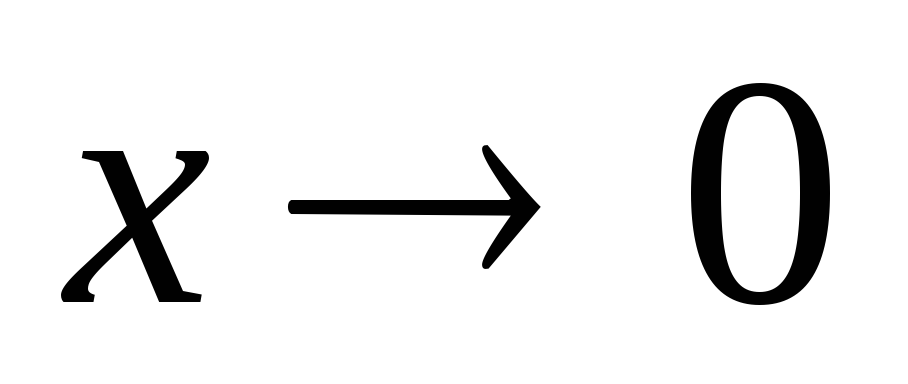1 – cos x~
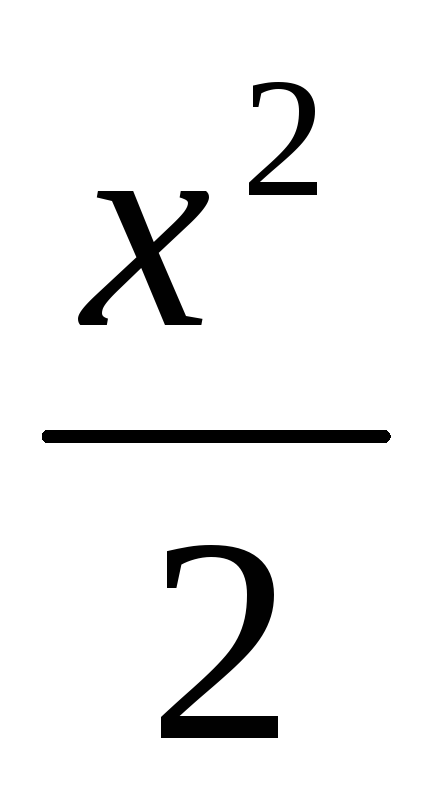при
; -
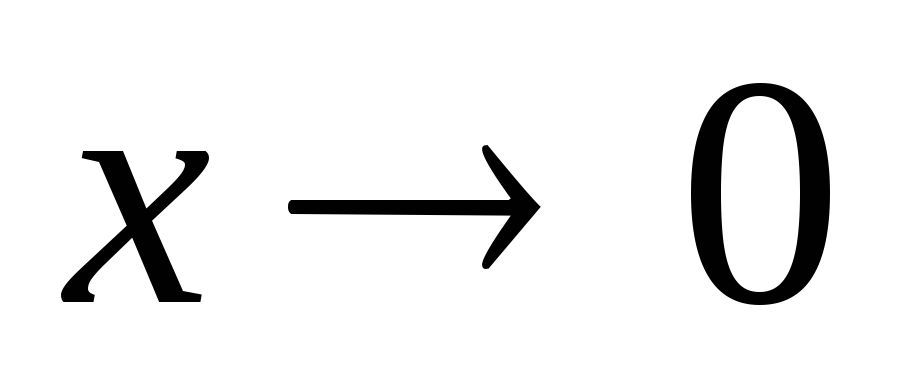e x – 1~x при
; -
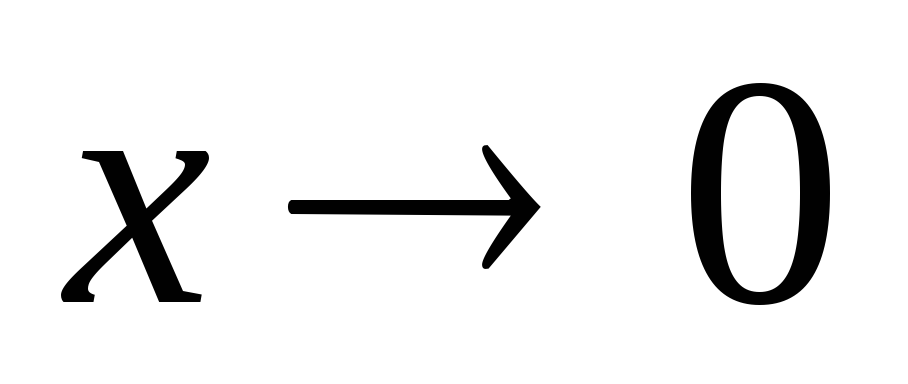a x – 1~x ln a при
; -
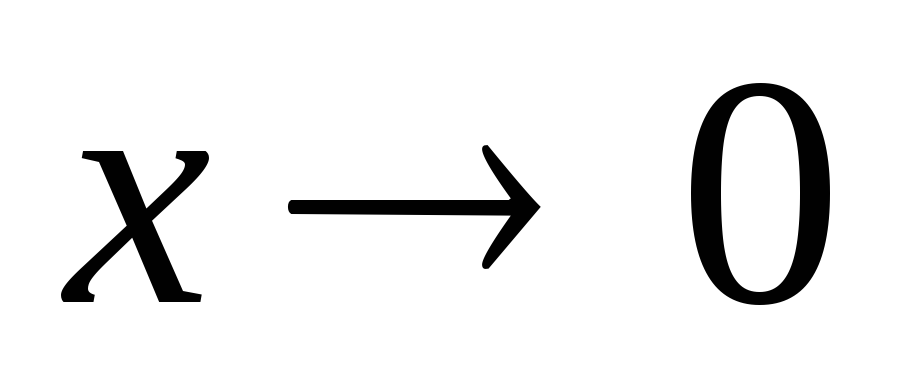ln(1+x)~x 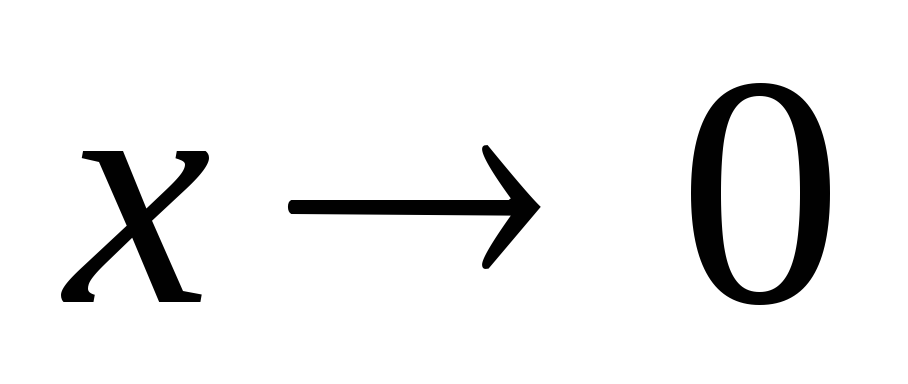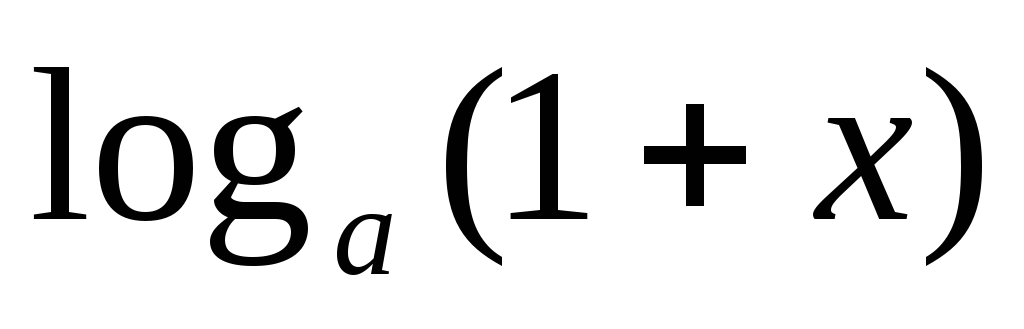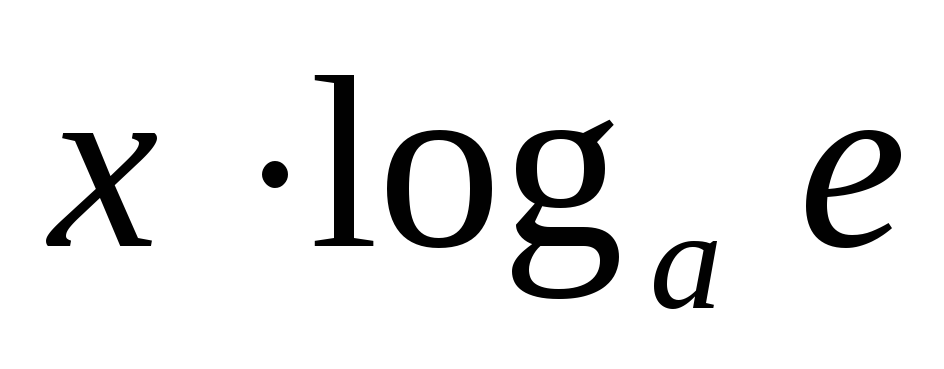при
; -
~
при
; -
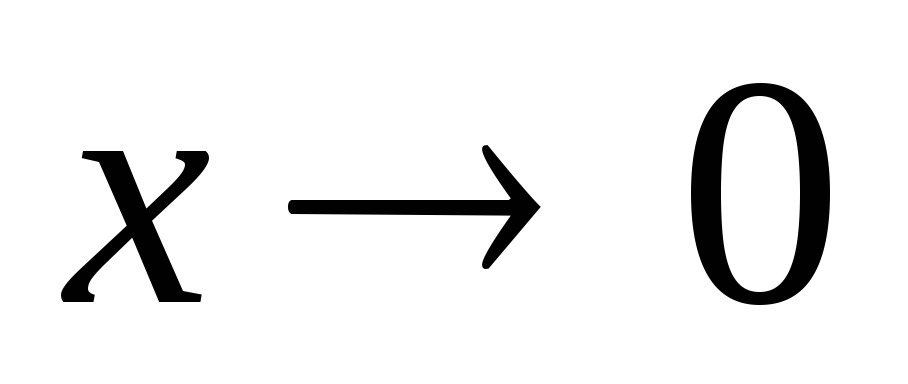(1+x)k – 1~k x, k>0 при
;
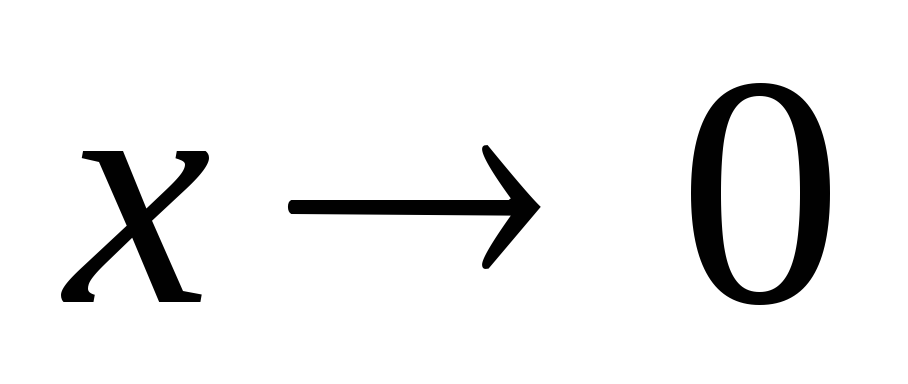в
частности,
~
.
Постановка
задачи: Вычислить предел
,
где f (x)
и g (x)
— бесконечно малые функции в точке
х =0.
План решения: Бесконечно малые функции, стоящие в числителе и знаменателе, следует заменить на им эквивалентные, используя основные эквивалентности (31).
Если f (x),
f1(x),
g (x),
g1(x)
— бесконечно малые функции в точке
х =0, такие, что f (x)~f1(x)
и g (x)~g1(x)
в точке х=0, и существует
,
то существует
,
причём
=
.
Постановка
задачи: Вычислить предел
,
где f (x)
и g (x)
— бесконечно малые функции в точке
х =а.
План решения:
1. Нужно заменить f (x)
и g (x)
на эквивалентные им бесконечно малые
функции. Но важнейшие эквивалентности
существуют при х=0. Поэтому сначала
сделаем замену переменной х – а= t
и будем искать предел при
.
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяя в произведении и частном бесконечно малые функции эквивалентными.
Постановка
задачи: Вычислить предел
,
где
и
.
План решения:
1. Преобразуем выражение под знаком
предела:
.
2. Поскольку показательная функция е х непрерывна, то можно перейти к пределу под знаком функции. Имеем:
=
=
.
3. Вычисляем
предел показателя
,
заменяя бесконечно малые функции
эквивалентными.
Постановка
задачи: Вычислить предел
,
где
и
.
План решения:
Чтобы использовать таблицу эквивалентных
бесконечно малых, сделаем замену
переменной t =x – a
(тогда
при
)
и преобразуем выражение под знаком
предела:
.
2. Поскольку
показательная функция ех
непрерывна, то можно перейти к пределу
под знаком этой функции. Имеем
=
.
3. При вычислении
предела
заменяем бесконечно малые функции
эквивалентными.
№15. Найти
пределы: 1)
;
2)
;
3)
;
4)
.
► 1)
=
=
=
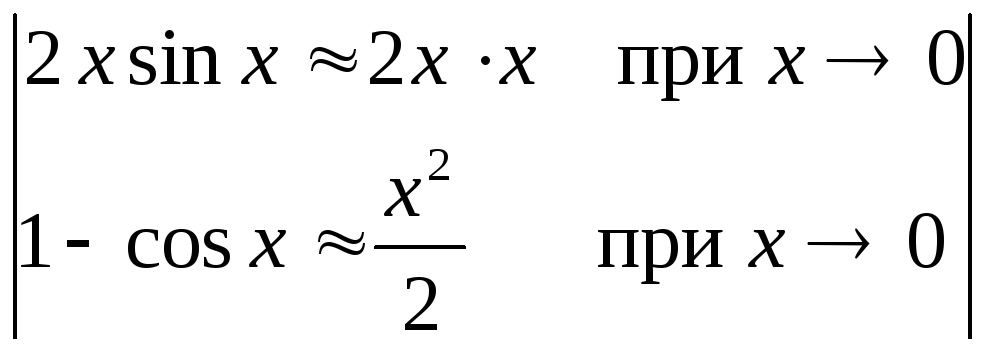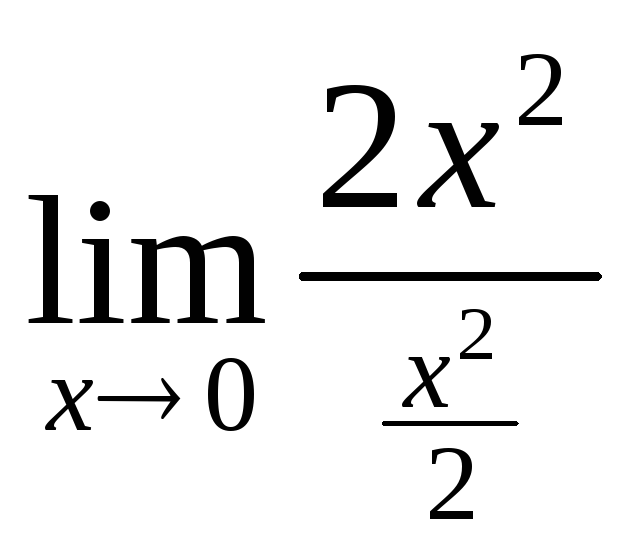=4;
2)
=
=
=
=
=
=
=
=
;
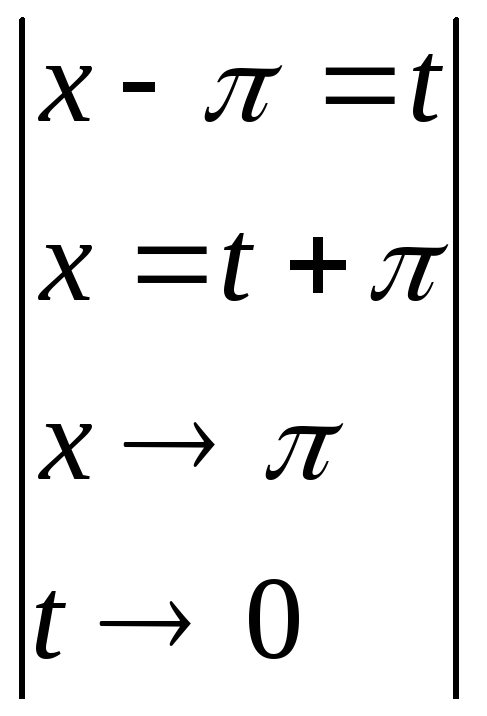3)
=
=
=
=
=
=
=
=
;
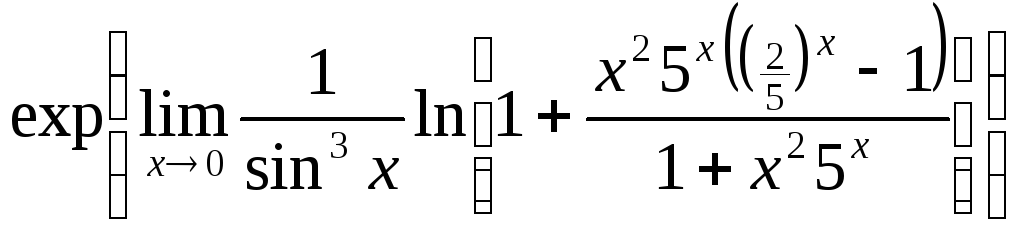4)
=
=
=
=
=
=
=
=
=
=
=
.
◄
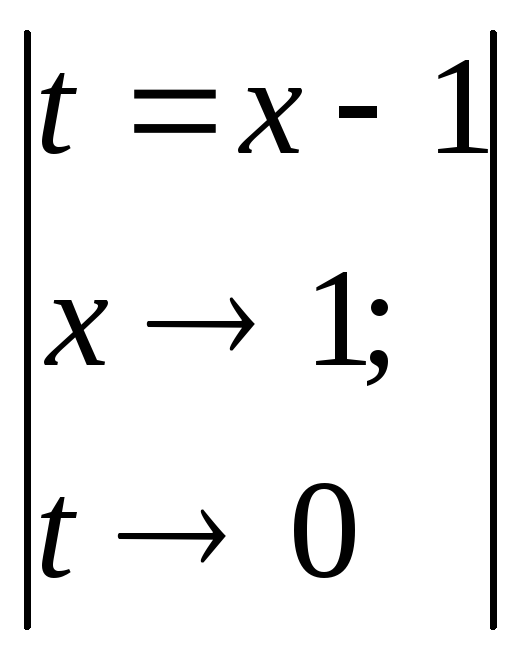Аудиторные задания
Найти пределы:
№161.
.
Ответ:
.
№162.
.
Ответ:
1.
№163.
.
Ответ:
3.
№164.
.
Ответ:
.
№165.
.
Ответ:
.
№166.
.
Ответ:
.
№167.
.
Ответ:
.
№168.
.
Ответ:
.