4.2 Биття

Розглянемо систему з двома ступенями свободи за умови близькості власних частот: . Тоді розв’язок (4.12) для узагальненої координати, наприклад,

(4.13)

можна записати у вигляді

(4.14)

Введемо позначення:

и ,

які називають «середньою» частотою і частотою «модуляції» відповідно. Замість (4.14) зручно записати

, (4.15)

де , – повільно мінливі періодичні функції часу.

Остаточно отримуємо замість (4.13) функцію

, (4.16)

де , ,

тобто рух носить синусоїдальний характер з амплітудою, що періодично повільно змінюється. Графік зміни зображений на рис. 4.5.

Рисунок 4.5 – Графік биття однієї узагальненої координати

Такі коливання називаються биттям. Рух, відповідний координаті , також відбувається за законом биття, але зрушеним по фазі щодо . Цей факт свідчить про обмін енергією між ступенями свободи.

Відзначимо, що в будь-якій системі з двома ступенями свободи можна створити биття.

4.3 Нормальні координати

Нормальними називаються узагальнені координати, які обрані таким чином, що кінетична енергія системи містить тільки квадрати узагальнених швидкостей, а потенційна енергія - квадрати узагальнених координат.

Якщо позначити нормальні координати через і , то

, а

і рівняння Лагранжа дають два незалежних диференціальних рівняння

Зв'язок між узагальненими координатами , , та нормальними , має вигляд

,

,

де коефіцієнти та визначаються з виразів кінетичної і потенційної енергій через узагальнені координати , і умов визначення і .

Коливання виду , і , називають нормальними коливаннями або нормальними модами. Ці поняття узагальнюються на системи з великим числом ступенів свободи, а також на системи з розподіленими параметрами. Нормальні координати мають, головним чином, теоретичне значення для доказу різних положень теорії коливань.

4.4 Резонанси в системі з двома ступенями свободи. Фільтри

Розглянемо вимушені коливання системи з двома ступенями свободи. У цьому випадку на точки системи, крім сил, що мають потенціал, діють збурювальні сили , які є деякими заданими функціями часу . Рівняння Лагранжа для даної системи мають вигляд

(4.17)

Приймаємо, що узагальнені збурювальні сили є простими гармонійними функціями часу, що мають однакову частоту і фазу , тобто

. (4.18)

Тоді диференціальні рівняння вимушених коливань цієї системи мають вигляд

(4.19)

Загальний інтеграл системи однорідних рівнянь, відповідних (4.19), вже нам відомий і характеризує вільні коливання системи (див. 4.12).

Частинні розв’язки системи (4.19) будемо шукати у вигляді

. (4.20)

Підставляючи (4.20) в рівняння (4.19) і скорочуючи на , отримуємо

(4.21)

З цієї системи маємо наступні вирази для амплітуд вимушених коливань:

(4.22)

Підставивши (4.22) в рівняння (4.20) встановлюємо наступне:

1. Вимушені коливання системи є гармонійними і мають частоту і фазу збурюючих сил.

2. Амплітуди вимушених коливань системи не залежать від початкових умов і визначається тільки властивостями системи і діючими на них силами.

Загальні інтеграли диференціальних рівнянь (4.19) тепер мають вигляд:

При цьому частоти і і коефіцієнти розподілу і нам уже відомі (див. (4.8), (4.9)). Так як знаменник у виразах для амплітуд (4.22) , є квадратним многочленом відносно , а корені цього многочлена є квадрати частот головних коливань системи і , то формули (4.22) можна представити у вигляді

(4.23)

При або амплітуди і зі збільшенням часу необмежено зростають, тобто маємо явище резонансу.

У разі резонансу вираз (4.20) не є частинним розв’язком системи диференціальних рівнянь вимушених коливань (4.19).

Для отримання частинного розв’язку у разі резонансу скористаємося головними координатами системи і .

Диференціальні рівняння вимушених коливань системи мають такий вигляд:

(4.24)

де .

Частинні розв’язки рівнянь (4.19) тепер мають вигляд

(4.25)

Переходячи до узагальнених координат і отримуємо, наприклад для :

(4.26)

Висновок: Наведене рівняння (4.26) показує, що у разі резонансу у вирази узагальнених координат входять члени, що містять час у вигляді множника перед тригонометричною функцією. Зі збільшенням часу ці члени необмежено зростають, що і відповідає явищу резонансу.

Визначимо тепер відношення амплітуд вимушених коливань

,

яке при і зберігає кінцеве значення і дорівнює:

при ,

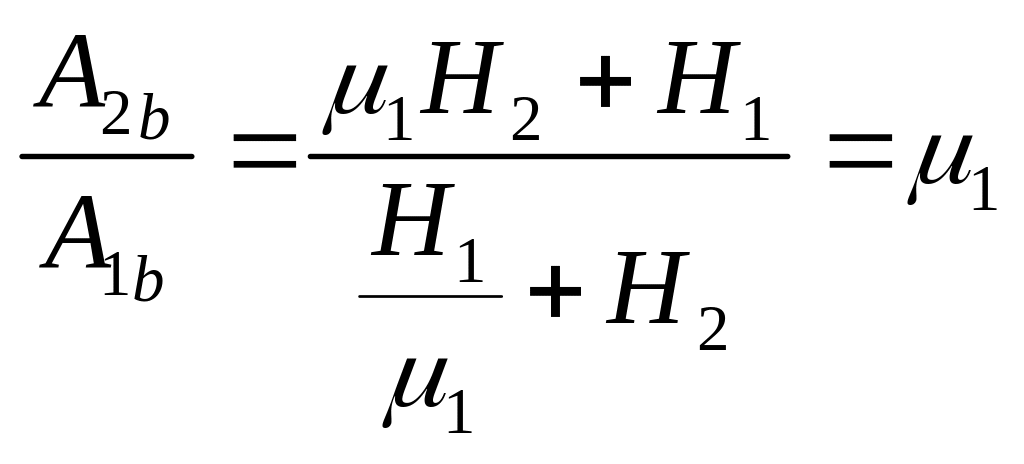при .

Висновок: отримані співвідношення показують, що у разі резонансу форми вимушених коливань системи аналогічні відповідним формам головних коливань.

Динамічний гаситель коливань (фільтр).

Розглянемо випадок, коли одна з узагальнених збурюючих сил дорівнює нулю. Покладемо, що

а .

Тоді при вираження амплітуд вимушених коливань (4.23) спрощуються і при , тобто при маємо

.

Висновок: таким чином при вимушені коливання, що відповідають першій узагальненій координаті, повністю гасяться.

На цьому принципі заснована теорія динамічних гасителів (фільтрів).