3.2.2 Дисипативний осцилятор з нелінійним загасанням

а) Випадок механічної системи з нелінійно-в'язким тертям. Метод енергетичного балансу.

Диференціальне рівняння руху має вигляд

. (3.7)

Наближений розв’язок рівняння вимушених коливань можна знайти методом енергетичного балансу, суть якого полягає в заміні нелінійної сили еквівалентною в енергетичному відношенні лінійною силою . Коефіцієнт визначається з умови рівності робіт, що здійснюються обома силами за один період, тобто

. (3.8)

Більше того, наближено приймаємо, що усталений розв’язок (3.7) як і у випадку лінійного тертя, має вигляд

. (3.9)

Записуючи рівняння (3.8) для напівперіоду (оскільки швидкість не змінює знак), і підставляючи (3.9) в (3.8), знаходимо

, (3.10)

де .

Якщо взяти для сили тертя нелінійний закон виду

,

то (3.10) дає значення

, (3.11)

де – ейлеров інтеграл другого роду.

Звертаючись до відомого розв’язку лінійної задачі (див. 3.1) знаходимо рівняння для амплітуди

; (3.12)

тут . Задаючись тепер конкретним значенням нелінійності “ ”, “ ”, можна побудувати при різних сімейство резонансних кривих.

б) Контур з нелінійним загасанням. Метод гармонійного наближення.

Схема контуру представлена ​​на рис. 3.7.

Рисунок 3.7 ­­– Схема контуру з нелінійним загасанням

Нехай

.

Тоді рівняння, що описує поведінку контура, в безрозмірному вигляді прийме вигляд

, (3.13)

де , , , , , , . У гармонійному наближенні розв’язок шукаємо у вигляді

. (3.14)

З (3.13) отримуємо систему для визначення , ,

, (3.15)

(3.16)

(3.17)

де .

Перше рівняння (3.15) дає величину постійної напруги зміщення на ємності за рахунок несиметрії нелінійного опору. Рівняння (3.16) і (3.17) дозволяють знайти амплітуду вимушених коливань

або

. (3.18)

Задаючись параметрами впливу і , сімейство резонансних кривих отримуємо з (3.18).

Залишаючи питання побудови резонансних кривих на самостійне дослідження, зазначимо лише на вимогу обережності в передбачуваних висновках про вимушені коливання у нелінійних системах внаслідок прийнятих припущень, покладених в основу знайдених розв’язань.

Наприкінці даного розділу вкажемо ще на один метод (метод повільно мінливих амплітуд) аналізу поведінки слабонелінейних систем при гармонійному зовнішньому впливі. З основами методу читач може ознайомитися у відомих навчальних посібниках [1-4].

Контрольні запитання і завдання до розділу 3

1. Яким чином можна знайти час встановлення коливань?

2. Час розгойдування системи більше за наявності або відсутності опору? Відповідь обгрунтуйте.

3. Чи залежить частота вимушених коливаннь від характерис-тик коливальної системи?

4. Отримайте розв’язок вимушених коливань системи без дисипації у разі резонансу.

5. Якою особливістю володіє залежність амплітуди вимушених коливань від частоти впливу, що збурює рух в нелінійних системах?

4 Коливання систем з двома ступенями свободи

4.1 Вільні коливання систем з двома ступенями свободи

Розглянемо вільні коливання механічної системи, що має два ступені свободи. Прикладами таких систем є: механічна система пов'язаних маятників (рис. 4.1), пов'язані електричні контури (рис. 4.2), трьохатомна молекула (рис. 4.3).

Рисунок 4.1– Пов'язані маятники

Рисунок 4.2 – Коливальні контури з індуктивним зв'язком

Рисунок 4.3 – Трьохатомна молекуда води

Використовуючи вирази кінетичної і потенційної енергій системи в узагальнених координатах і , рівняння Лагранжа призводять до диференціальних рівнянь вільних коливань виду

(4.1)

Уявімо систему (4.1) у формі

(4.2)

звідки видно, що ліві частини є рівняннями лінійних консервативних систем, а праві частини характеризують сили зв'язку між ними. Коефіцієнти , характеризують зв'язок між так званими парціальними системами.

Будь-яку складну систему з двома ступенями свободи можна розглядати як систему, що складається з двох окремих систем з одним ступенем свободи, пов'язаних одна з однією. Ці окремі системи називають парціальними. Зв'язність систем означає, що коливання в одній системі впливають на коливання в інший і навпаки.

Приймемо для подальшого вивчення коливання системи, що парціальна система, відповідна даної незалежної координаті, отримана з повної, коли всі координати системи, крім данної, рівні тотожно нулю.

З (4.2) видно, що парціальні частоти рівні

, .

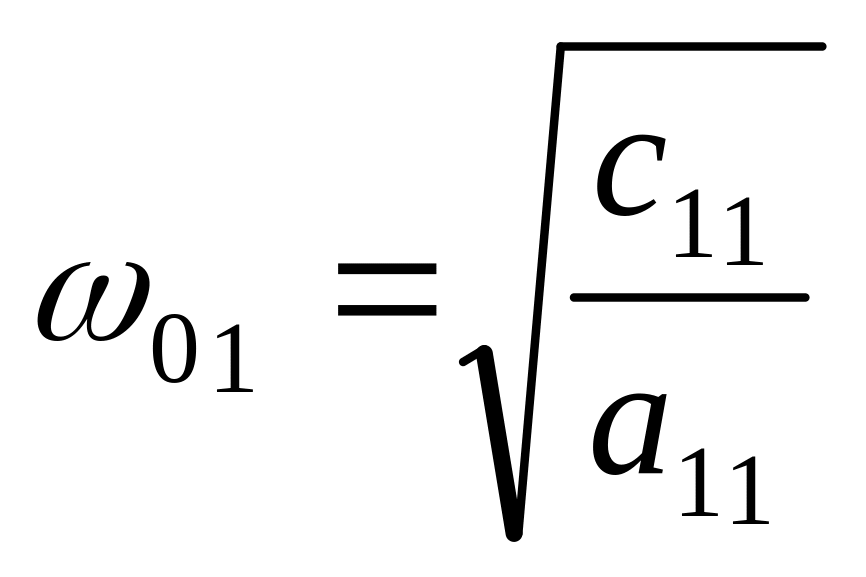З властивостей позитивної визначеності квадратичних форм Т та П випливає, що

(4.3)

(критерій Сильвестра).

Частинні розв’язки системи (4.1) шукаємо у вигляді простого гармонійного закону:

, . (4.4)

Підставляючи (4.4) в рівняння (4.1), одержимо рівняння для амплітуд

(4.5)

Позначимо відношення узагальнених координат, рівне відношенню амплітуд коливань, через

. (4.6)

Нетривіальний розв’язок системи (4.5) буде тільки в тому випадку, коли її визначник дорівнює нулю, що дає рівняння власних частот коливань

. (4.7)

або

(4.8)

Досліджуємо функцію . Коефіцієнт при (див. 4.8) і вільний член більше нуля згідно критерію Сильвестра (4.3): це означає, що графік функції є парабола з вітками, спрямованими вгору. З (4.8) видно, що при рівної однієї з парціальних частот та . Корені рівняння (4.8) визначають власні частоти системи.

Зобразимо графік функції (рис. 4.4).

Рисунок 4.4 – Закон розподілу власних частот системи

Графік ілюструє відому теорему Релея: нижча частота власних коливань системи завжди менше найменшої парціальної частоти , а вища частота завжди більше найбільшої парціальної частоти .

Відповідні частотам і коливання називають головними коливаннями системи. Меншу з частот називають основною частотою, а перше головне коливання називають основним коливанням (воно є основним у результуючому русі системи). Визначивши і , з рівняння (4.8) знайдемо два значення , відповідні кожному з головних коливань:

(4.9)

Величини , характеризують форми головних коливань і їх називають коефіцієнтами розподілу амплітуд, тобто вони показують у скільки разів амплітуда відповідного коливання в одній з координат більше (або менше) амплітуди іншої координати.

Позначивши значення узагальнених координат і амплітуд коливань, відповідних першому головному коливанню, індексом (1), маємо

(4.10)

для другого головного коливання - індексом (2), то

(4.11)

Загальний розв’язок системи диференціальних рівнянь (4.1) виходить шляхом підсумовування частинних розв’язків

(4.12)

де , , і знаходяться з початкових умов.

Висновки:

1. Розв’язок (4.12) показує, що кожне з головних коливань окремо є простим гармонійним коливанням, але результуючий рух являє собою складний рух.

2. Якщо система здійснює одне з головних коливань (див. 4.12), то обидві узагальнені координати змінюються синхронно, тобто мають однакові частоти і фази коливань.

3. У кожному з головних коливань амплітуди знаходяться в постійному співвідношенні ( або ), що не залежить від початкових умов і залежить тільки від структури системи.