7.3. Комбінаційні арифметичні вузли

7.3.1. Загальна характеристика арифметичних вузлів. Арифметично-логічний пристрій (АЛП) процесора виконує арифметичні і логічні операції над багаторозрядними двійковими словами. До складу АЛП входять блоки призначені для виконання арифметичних операцій над числами в форматах з фіксованою крапкою, плаваючою крапкою та десятковому форматі. Важливою частиною цих блоків є цифрові вузли, що виконують елементарні математичні операцій: додавання, віднімання, множення, ділення і порівняння двійкових чисел. Такі вузли будують на основі логічних елементів, як комбінаційні схеми, тому вони мають назву комбінаційні арифметичні вузли.

Особливістю двійкової арифметики є те, що чотири арифметичні дії в ній можна звести до двох операцій  додавання і зсуву. Тому основу арифметичних вузлів складають суматори. Суматором називають функціональний вузол комп’ютера, призначений для додавання двох n-розрядних двійкових слів (чисел). Такі вузли будують на базі елементарних цифрових вузлів, здатних виконувати операцію додавання в одному розряді двійкового числа, тобто додавати два однобітових числа. До таких однорозрядних арифметичних вузлів відносяться напівсуматор і повний суматор

За способом додавання суматори поділяють на паралельні, послідовні та паралельно-послідовні. У паралельних n-розрядних суматорах значення всіх розрядів операндів надходять у паралельному коді одночасно на відповідні входи суматора, кількість яких визначає розрядність двійкових чисел, що додаються. Послідовні суматори виконують операцію додавання операндів представлених у послідовному коді. Для виконання операції додавання вони використовують один однорозрядний суматор, на входи якого, в кожному такті, поступають значення розрядів операндів послідовно в напрямку від молодших розрядів до старших, а перенесення, що запам’ятовується у попередньому такті за допомогою тригера, враховується при формуванні значення однорозрядної суми в поточному такті. Складовою частиною послідовних n-розрядних суматорів є регістри зсуву, тому такі суматори не є комбінаційними цифровими вузлами. В паралельно-послідовних суматорах n-розрядні числа розбиваються на частини по k розрядів. Кожна з цих частин подається у паралельному коді на входи k-розрядного суматора (одночасно у всіх розрядах), а самі частини – послідовно, роздільно у часі, в напрямку від молодших частин до старших з урахуванням перенесення, яке запам’ятовується.

За схемотехнічними ознаками і особливостями формування результату операції додавання суматори поділяють на комбінаційні і накопичувальні. Комбінаційні суматори не містять елементів пам’яті і реалізуються, як комбінаційні схеми. Накопичувальні суматори являють собою поєднання комбінаційного суматора і регістра. Такі суматори працюють згідно співвідношенню S := S+A („:=” – символ присвоювання), тобто до попереднього значення суми S, що зберігається у регістрі, додається черговий доданок А і результат заміщає старе значення суми у регістрі.

За способом організації перенесення між розрядами суматори поділяють на суматори з послідовним, паралельним, наскрізним та груповим перенесеннями. Спосіб перенесення визначає час виконання операції додавання. Суматори з послідовним перенесенням схемотехнічно організовані досить просто, але мають низьку швидкодію порівняно з суматорами з паралельним перенесенням, які схемотехнічно організовані значно складніше.

За системою числення суматори поділяють на двійкові і десяткові. Двійкові суматори виконують операцію складання двійкових операндів представлених у знаковому і беззнаковому форматі з фіксованою крапкою (див. підрозділ 7.2.8). В десяткових суматорах для подання операндів використовується двійково-десятковий код (див. підрозділ 1.2). Такі суматори будують з урахуванням правил десяткової арифметики на основі двійкових суматорів, які виконують операцію додавання двійкових тетрад, які відображують десяткові цифри в двійково-десятковому коді.

При побудові арифметичних вузлів комп’ютера на основі двійкових суматорів враховують, що операція віднімання може бути замінена додаванням двійкових операндів у оберненому або доповняльному коді, а операції множення та ділення можна звести до багаторазового додавання та зсування. Отже розглянемо принципи побудови арифметичних вузлів комп’ютерної електроніки.

7.3.2. Однорозрядні двійкові суматори. Такі суматори виконують додавання однорозрядних двійкових чисел. В залежності від можливості враховувати перенесення в результаті операції їх поділяють на напівсуматор і повний суматор.

A	B	S	P
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

а

б

Рис. 7.29. Напівсуматор: умовне графічне зображення (а); таблиця справжності (б)

Напівсуматор не враховує перенесення. Він має два входи на які подаються однорозрядні операнди A і B та два виходи, на яких формується сума S і значення перенесення P. Такий елементарний суматор при побудові багаторозрядних суматорів може бути використаним тільки у молодшому розряді, де перенесення відсутнє. Умовне графічне зображення напівсуматора і його таблиця справжності, побудована з урахуванням правил двійкової арифметики, наведені на рис. 7.29. З таблиці справжності випливає, що функції виходів напівсуматора S і P описують логічні рівняння:

S = B + A = AB; P = AB. (7.34)

Схеми напівсуматора в булевому базисі і базисі Жегалкіна, побудовані на підставі (7.34), показані на рис. 7.30.

Рис. 7.30. Схеми напівсуматора в булевому базисі (а)

та базисі Жегалкіна (б)

Повний суматор враховує перенесення, тому має три входи: А і B для однорозрядних операндів і вхід перенесення P₀. Як й напівсуматор, повний суматор на двох своїх виходах формує значення суми S і перенесення P від операції додавання, яку він виконує. Умовне зображення повного суматора показано на рис. 7.31а. Завдяки здатності враховувати перенесення повний суматор при побудові на його основі n-розрядних суматорів може бути використаний у будь-якому i-тому розряді такого суматора. В цьому випадку функції виходів повного суматора i-того розряду S_i і P_i залежать від значення розрядів A_i, B_i багаторозрядних операндів і значення перенесення P_i-1 з сусіднього молодшого i-1-го розряду (рис. 7.31а).

Ai	Bi	Pi-1	Pi	Si
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 1 0 1 1 1	0 1 1 0 1 0 0 1

а

б

Рис. 7.31. Повний суматор: умовне графічне зображення (а);

таблиця справжності (б)

Таблиця справжності для функцій P_i(A_i,B_i,P_i-1), S_i(A_i,B_i,P_i-1), побудована з урахуванням правил двійкової арифметики, наведена на рис. 7.31б, а результати мінімізації методом Вейча показані на рис. 7.32а. З них випливає, що склеювання одиниць має місце тільки для функції P_i(A_i,B_i,P_i-1). Її логічне рівняння, отримане за результатами склеювання, має вигляд:

P_i = A_iB_i + B_iP_i-1 + A_iP_i-1, (7.35)

а логічне рівняння для функції виходу S_i повного суматора у ДДНФ можна записати як

. (7.36)

а	б
Рис. 7.32. Результати мінімізації методом Вейча функцій виходів повного суматора (а) і функції його виходу S, як булевої функції чотирьох змінних (б)

Із співвідношень (7.35), (7.36) випливає, що для побудови схеми повного суматора в булевому базисі потрібні 3 інвертори, чотири елемента 3І, три елемента 2І, один елемент 4АБО і один 3АБО, тобто всього 12 елементів. Схему повного суматора можна спростити, скоротивши кількість логічних елементів, якщо виконати мінімізацію S_i, розглянувши цю функцію як частково визначену БФ чотирьох змінних S_i(A_i,B_i,P_i-1,P_i). Результати такої мінімізації представлені на рис. 7.32б. З них випливає наступне логічне рівняння:

. (7.37)

В цьому випадку, з урахуванням (7.35), для побудови схеми повного суматора потрібен тільки один інвертор, шість елементів 2І, один 3І, один елемент 4АБО і один 3АБО, тобто всього 10 логічних елементів. Така схема наведена на рис. 7.33. Її особливістю є наявність зворотного зв’язку між виходом перенесення P_i і схемою формування однорозрядної суми S_i. Наслідком цього є те, що швидкодія формування суми менша за швидкодію формування перенесення, оскільки час затримки сигналу P_i визначається тільки сумою затримок поширення сигналу елемента І та АБО, а час затримки формування суми S_i  сумою затримок перенесення P_i і поширення сигналу в логічних елементах НЕ, І та АБО. Тому параметри швидкодії повного суматора визначаються співвідношеннями:

t_зпP = t_зпI + t_зпАБО; t_зпS = 2t_зпI + 2t_зпАБО + t_зпНЕ. (7.38)

Рис. 7.33. Схема повного

суматора в булевому базисі

7.3.3. Багаторозрядні двійкові суматори. Розглянуті вище однорозрядні суматори використовують для побудови багаторозрядних суматорів, призначених для додавання n-розрядних двійкових чисел, які будемо позначати як: А = A_nA_n-1…A_i…A₂A₁, B = B_nB_n-1…B_i…B₂B₁. Звичайно такі суматори будують на основі повних суматорів, що дозволяють враховувати у сумі поточного розряду перенесення із сусіднього молодшого розряду. Для побудови n-розрядного паралельного суматора, очевидно, потрібно n однорозрядних повних суматорів.

Найпростішим за схемотехнічною організацією є паралельний суматор з послідовним перенесенням, схема якого та умовне зображення показані на рис. 7.34.

Значення всіх розрядів чисел A і B поступають на входи відповідних однорозрядних суматорів одночасно, а сигнал перенесення передається від розряду до розряду послідовно у часі, починаючи від молодшого розряду суми S₁ до її старшого розряду S_n.

У паралельних суматорах з послідовним перенесенням час виконання операції складання t_ у найгіршому випадку, коли сигнал перенесення послідовно розповсюджується від першого до n-того розряду, визначається співвідношенням:

t_ = (n-1)t_зпP + t_зпS, (7.39)

де значенням t_зпP і t_зпS для повних суматорів реалізованих за схемою на рис. 7.33 задаються співвідношеннями (7.38).

а	б
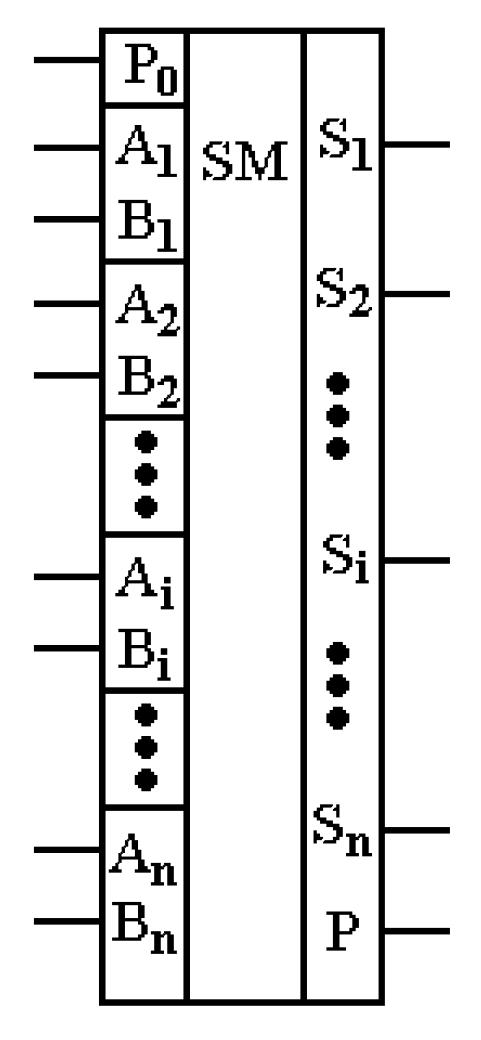
Рис. 7.34. Схема паралельного суматора з послідовним перенесенням (а) і умовне зображення n-розрядних суматорів(б)

Коли кількість розрядів n паралельних суматорів з послідовним перенесенням зростає їх швидкодія зменшується. Це недолік таких суматорів. Для підвищення швидкодії в суматорах застосовують схеми прискореного  паралельного перенесення, тому такі суматори називають паралельними суматорами з паралельним перенесенням.

Схеми прискорених переносів виробляють сигнали перенесення P_i одночасно для всіх розрядів суматора. Сигнал P_i для даного розряду формується такими схемами з урахуванням всіх змінних необхідних для вироблення перенесення, тобто тих, від яких залежить його наявність або відсутність. Такими змінними є зовнішнє перенесення P₀ та значення всіх розрядів доданків, які є молодшими відносно даного розряду. З урахуванням цього структура n-розрядного суматора з паралельним перенесенням має вигляд, показаний на рис. 7.35. Тут схеми прискорених переносів позначені як CR (від англійського слова carry  перенесення), а для повних суматорів SM вихід переносу не показаний, оскільки він не приймає участі у формуванні значення суми.

Для визначення логічної структури схем прискореного переносу CR_i використовують дві допоміжні функції: генерації і прозорості.

Функція генерації приймає одиничне значення, коли перенесення на виході даного розряду з’являється незалежно від наявності або відсутності вхідного перенесення. Це має місце колі обидва доданки A_i і B_i дорівнюють одиниці, тому функцію генерації можна представити кон’юнкцією g_i = A_iB_i.

Рис. 7.35. Структура суматора з паралельним перенесенням

Функція прозорості приймає одиничне значення, коли перенесення в даному розряді з’являється тільки при наявності сигналу перенесення на вході повного суматора цього розряду. Це має місце, коли хоча б один з доданків A_i чи B_i приймає одиничне значення, тобто функцію прозорості можна представити у вигляді виключального АБО (суми за модулем 2) h_i = = A_i  B_i. Аналіз можна спростити, якщо виключальне АБО замінити диз’юнкцією, тобто функцію прозорості записати у вигляді h_i = A_i + B_i. Підставою для такої заміни є те, що перенесення буде виникати і у випадку, коли обидва доданки дорівнюють одиниці.

З урахуванням викладеного вище вираз для функції перенесення P_i в будь-якому i-тому розряді суматора можна записати у вигляді:

P_i = g_i + h_iP_i-1. (7.40)

На підставі (7.40) для функцій перенесення різних розрядів суматора можна отримати наступну систему рівнянь:

P₁ = g₁ + h₁P₀;

P₂ =g₂ +h₂(g₁ + h₁P₀) = g₂ +h₂g₁ + h₂h₁P₀;

P₃ = g₃ + h₃(g₂ + h₂(g₁ + h₁P₀)) =

= g₃ + h₃g₂ + h₃h₂g₁ + h₃h₂h₁P₀;

(7.41)

P_i = g_i + h_ig_i-1 + h_ih_i-1g_i-2 + h_ih_i-1h _i-2g_i-3 +…+h_ih_i-1…h₂g₁ +

+h_ih_i-1…h₂h₁P₀,

де P₀ – значення вхідного перенесення суматора.

Побудову схеми суматора з паралельним перенесенням розглянемо на прикладі чотирьохрозрядного суматора. Функції перенесення такого суматора описуються першими трьома рівняннями системи (7.41). На підставі закону де Моргана приведемо ці рівняння до базису ІНЕ:

(7.42)

На рис. 7.36 показано варіант схеми паралельного суматора з паралельним перенесенням, яка побудована згідно (7.42), з урахуванням, що h_i = A_i + B_i (i = 1, 2, 3).

Рис. 7.36. Схема чотирьохрозрядного суматора

з паралельним перенесенням

Хоча кількість логічних елементів схеми прискореного перенесення зростає в старших розрядах суматора, в будь-якому розряді вона має три рівня затримки. Це означає, що на відміну від суматора з послідовним перенесенням значення бітів суми формуються одночасно для всіх двійкових розрядів, тому час виконання операції складання t_ не залежить від кількості розрядів суматора і визначається співвідношенням:

t_ = 3t_зп + t_зпS, (7.43)

де t_зп  час затримки поширення сигналу логічних елементів АБО та ІНЕ схеми прискореного перенесення (для спрощення прийнято, що ці елементи мають однакову затримку поширення сигналу, яка дорівнює t_зп), t_зпS – час затримки поширення повного суматора.

Отже перевагою суматорів з паралельним перенесенням є висока швидкодія, що не залежить від кількості розрядів суматора. Недолік полягає в ускладненні схеми, порівняно з суматорами з послідовним перенесенням (рис. 7.34а). Окрім того із зростанням кількості розрядів суматора, зростає кількість входів логічних елементів ІНЕ схеми прискореного перенесення, а оскільки вона обмежена значенням K_об = 8, суматори, побудовані за схемою, яка наведена на рис. 7.36, не можуть мати більше восьми розрядів. При побудові суматорів з більшою розрядністю використовують комбіноване паралельно-послідовне перенесення.

Один з можливих способів нарощування розрядності суматорів показано на рис. 7.37. У випадку, коли для нарощування використані суматори з паралельним перенесенням, схема, що наведена на рис. 7.37, є суматором з паралельно-послідовним перенесенням, у випадку використання суматорів з послідовним перенесенням ця схема  суматор с послідовним перенесенням.

Рис. 7.37. Нарощування розрядності суматорів

При нарощуванні розрядності для організації паралельного перенесення між суматорами можуть бути використані схеми прискореного перенесення, які випускаються як самостійні вироби у складі деяких серій інтегральних мікросхем. Для прикладу наведемо чотирьохрозрядні мікросхеми прискореного перенесення КР1533ИП4 (SN74LS182), КР1531ИП4 (74F182).

Рис. 7.38. Умовне графічне зображення мікросхеми КР1594ИМ6

Двійкові суматори входять до складу серій інтегральних мікросхем ТТЛШ і КМОНТЛ. На рис. 7.38, як приклад, показано умовне графічне зображення і цокольовка мікросхеми комплементарної МОН-транзисторної логіки КР1594ИМ6 (функціональний аналог HD74ACT283). Це чотирьохрозрядний суматор з паралельним перенесенням сумісний за рівнями напруги і струмами навантаження з мікросхемами ТТЛШ. Параметри деяких мікросхем чотирьохрозрядних суматорів з паралельним перенесенням наведені в табл. 7.7.

Таблиця 7.7

Параметри інтегральних мікросхем суматорів ТТЛШ і КМОПТЛ

Параметр		Мікросхеми та їх функціональні аналоги
		КР1531ИМ6 (74F283)	К561ИМ1 (CD4008BMS)	КР1554ИМ6 (HD74AC283)	КР1594ИМ6 (HD74ACT283)
Uсс, В		4,5÷5,5	5÷20	2÷6	2÷6
I^1сп, (IccH), мА		36	0,01 (15 В)	0,008 (5,5 В)	0,008 (5,5 В)
I^0сп, (IccL), мА		36
U^0вих, (UОL), В		≤ 0,5	≤ 0,05	≤ 0,1	≤ 0,1
U^1вих, (UОH), В		 2,5	Uсс  0,05	Uсс  0,1	Uсс  0,1
I^1вх (IIH), мкА		5	0,1	0,1	0,1
I^0вх (IОL), мА		1,2	110^-4	110^-4	110^-4
I^0вих (IОL), мА		≤ 60	≤ 2,4	≤ 50	≤ 50
tPLH, нс	P0Si	7,0 7,0	310 (10 В)	9,5 (5 В) 8,5 (5 В)	11,5 (5 В) 10,0 (5 В)
tPHL, нс
tPLH, нс	Ai або BiSi	7,0 7,0	320 (10 В)	11,5 (5 В) 11,0 (5 В)	13,0 (5 В) 12,0 (5 В)
tPHL, нс
tPLH, нс	P0P	5,7 5,4	100 (10 В)	7,5 (5 В) 8,0 (5 В)	9,0 (5 В) 10,0 (5 В)
tPHL, нс

Нагадаємо, що значення напруги, вказані в табл. 7.7 в дужках, відповідають напрузі живлення, при якій був виміряний відповідний параметр інтегральної мікросхеми.

7.3.4. Двійково-десятковий суматор. Суматори багаторозрядних десяткових чисел будують на основі елементарних однорозрядних двійково-десяткових суматорів, що виконують операцію складання двійкових тетрад, які відображують десяткові цифри в двійково кодованій десятковій системі числення (див. підрозділ 1.2). Тому однорозрядний двійково-десятковий суматор можна реалізувати на основі чотирьохрозрядних двійкових суматорів. Такий однорозрядний двійково-десятковий суматор повинен формувати значення однорозрядної десяткової суми в двійково-десятковому коді і значення десяткового перенесення P₁₀ з урахуванням правил десяткової арифметики.

Оскільки при додаванні тетрад двійково-десяткового коду значення суми може перевищувати число 9₁₀ = 1001₂, потрібна корекція результату. Така корекція повинна виконуватись при виникненні десяткового перенесення (P₁₀ = 1), шляхом віднімання від тетради результату числа 10₁₀ = 1010₂. Оскільки в двійковій арифметиці віднімання заміняється додаванням у доповняльному коді, корекція результату може бути здійснена шляхом додавання до результату доповняльного коду числа мінус десять, тобто [1010₂]_д = 0110₂. Отже для побудови однорозрядного десяткового суматора потрібні два чотирьохрозрядних двійкових суматори, один з яких буде додавати двійкові тетради десяткових цифр, а другий – здійснювати корекцію результату.

Для визначення схеми формування десяткового перенесення розглянемо P₁₀, як функцію змінних S₄, S₃, S₂, S₁ на виході суматора, який додає тетради десяткових цифр. Цю функцію описує таблиця справжності на рис. 7.39а, а її мінімізація методом діаграм Вейча показана на рис. 7.39б.

S₄

S3	S2	S1	P10
0	0	0	0	0
				0
1	0	0	1	0
1	0	1	0	1
1	0	1	1	1
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

а

б

Рис. 7.39. Таблиця справжності для функції десяткового

перенесення P₁₀ (а) і результати її мінімізації методом

діаграм Вейча (б)

Результат мінімізації можна записати у вигляді логічного рівняння:

P₁₀ = S₄S₃ + S₄S₂. (7.44)

Слід зазначити, що десяткове перенесення виникає також при значеннях суми тетрад 16₁₀, 17₁₀ і 18₁₀, коли на виході P чотирьохрозрядного двійкового суматора, який додає тетради виникає двійкове перенесення P = 1, тому співвідношення (7.44) треба доповнити:

P₁₀ = S₄S₃ + S₄S₂ + P = . (7.45)

З урахуванням вище викладеного та співвідношення (7.45) можна побудувати схему однорозрядного двійково-десяткового суматора (рис. 7.40). Тетради двійкового коду десяткових цифр подаються на входи A₁A₄ і B₁B₄ суматора DD1. Якщо при додаванні тетрад P₁₀ = 0, то суматор DD2 додає до результату число 0000₂ і він передається на вихід без зміни. При виникненні десяткового перенесення P₁₀ = 1 до результату складання тетрад додається число 0110₂, тобто відбувається десяткова корекція суми.

Рис. 7.40. Схема однорозрядного

двійково-десяткового суматора

На базі однорозрядних двійково-десяткових суматорів (рис. 7.40) нескладно побудувати багаторозрядний паралельний десятковий суматор з послідовним перенесенням шляхом об’єднання виходів P₁₀ і входів P₀ суматорів сусідніх розрядів у напрямку від молодших десяткових розрядів до старших. В такому суматорі тетради двійково-десяткового коду одночасно подаються на входи відповідних однорозрядних двійково-десяткових суматорів.

7.3.5. Реалізація операції віднімання на двійкових суматорах. В двійковій арифметиці операція віднімання чисел А = A_nA_n-1…A_i…A₂A₁, B = B_nB_n-1…B_i…B₂B₁ може бути замінена операцією додавання, якщо від’ємник представити у оберненому або доповняльному коді. Дійсно, різницю двох чисел можна записати як A  B = A + (B), звідкіля випливає, що різниця може бути замінена алгебраїчною сумою зменшуваного і негативного від’ємника. Оскільки для подання від’ємних чисел в цифровій техніці використовують обернений і доповняльний коди (див. підрозділ 7.2.8), то у загальному випадку різницю двох чисел можна записати як

A – B = A + [B]_з = A + [B]_д =

= A_nA_n-1…A_i…A₂A₁ + = (7.46)

= A_nA_n-1…A_i…A₂A₁ + +1.

При виконанні операції віднімання в оберненому коді треба враховувати циклічне перенесення, тобто при наявності перенесення зі старшого біту суми до результату треба додати одиницю, у доповняльному коді циклічне перенесення не враховують. Зазначимо також, що при поданні чисел у знаковому форматі з фіксованою крапкою, операція порозрядного складання виконується однаковим чином, як над цифровими бітами, так і над знаковим бітом формату. Результат операції віднімання буде у тому коді, який використовується для подання від’ємника.

З урахуванням викладеного вище і (7.46) для реалізації на суматорах арифметичної операції віднімання біти зменшуваного треба подати на входи суматора безпосередньо, а від’ємника – через інвертори. Якщо операція виконується у оберненому коді, вихід перенесення суматора P з’єднують з його входом P₀ для реалізації циклічного перенесення. При виконанні операції віднімання в доповняльному коді на вхід перенесення суматора P₀ подають логічну одиницю, підсумовування якої до оберненого коду, що надходить з виходів інверторів, забезпечує доповняльний код від’ємника.

На рис. 7.41 наведені схеми увімкнення суматорів для реалізації віднімання чотирьохрозрядних двійкових чисел A = A₄A₃A₂A₁ і B = B₄B₃B₂B₁.

Зазначимо, що числа A і B, що надходять на входи суматорів (рис. 7.41) можуть бути представлені, як у беззнаковому, так і у знаковому форматі з фіксованою крапкою. У випадку знакового формату біти чисел A₄ і B₄ будуть знаковими, а знак результату буде відображати біт суми S₄.

а	б
Рис. 7.41. Схеми увімкнення суматора для виконання операції віднімання в оберненому (а) і доповняльному (б) кодах

Якщо в схемах на рис. 7.41 інвертори замінити на логічні елементи сума за модулем 2, то можна реалізувати арифметичний вузол, який в залежності від керуючого сигналу виконує або операцію складання або операцію віднімання. Схема такого вузла показана на рис. 7.42.

Рис. 7.42. Схема арифметичного вузла для виконання операцій

складання і віднімання

При наявності на вході керування In низького рівня напруги U⁰ (In = P₀ = 0) елементи „сума за модулем 2” працюють як повторювачі, тому операнд B передається на входи суматора без зміни і вузол виконує операцію складання A + B. Коли сигнал на вході In має високий рівень U¹ (In = 1), елементи „сума за модулем 2” працюють як інвертори. Операнд B передається на входи суматора в оберненому коді, а підсумовування одиниці P₀ = In = 1 забезпечує виконання операції віднімання з результатом у доповняльному коді.

7.3.6. Матричні помножувачі. Арифметично-логічні пристрої сучасних комп’ютерів виконують арифметичну операцію множення не мікропрограмним, а апаратним шляхом. Добуток двійкових чисел апаратним шляхом можна отримати за допомогою матричних помножувачів. Такі цифрові вузли будують на основі суматорів і елементарних помножувачів, що формують добуток M однорозрядних двійкових чисел Aі B.

Для визначення схеми однорозрядного помножувача розглянемо арифметичний добуток M, як булеву функцію логічних змінних A, B. Таблиця справжності функції M, побудована з урахуванням правил двійкової арифметики для операції множення, наведена на рис. 7.43а. З неї випливає, що арифметична операція множення однорозрядних двійкових чисел співпадає з логічною операцією кон’юнкція. Саме тому кон’юнкцію називають логічним множенням.

A

B	M
0 0 1 1	0 1 0 1	0 0 0 1

а

б

Рис. 7.43. Таблиця справжності однорозрядного двійкового помножувача (а) і його схема (б)

Таким чином арифметичне множення двох однорозрядних двійкових чисел можна реалізувати на логічному елементі 2І (рис. 7.43б). Побудову помножувачів багаторозрядних двій-кових чисел розглянемо на прикладі множення цілих чисел, а саме чотирьохрозрядного числа A = A₄A₃A₂A₁ і двохрозрядного числа B = B₂B₁. Будемо вважати, що числа представлені в беззнаковому форматі з фіксованою крапкою, тобто всі біти формату є цифровими. Саме в беззнаковому форматі виконується сама процедура множення чисел в АЛП комп’ютера, для чого попередньо числа у знаковому форматі перетворюються у беззнаковий формат, а знак добутку визначається з урахуванням значення знакових бітів співмножників.

Структура матричних помножувачів тісно пов’язана зі структурою математичних виразів, що описують операцію множення, зокрема з відомою схемою „множення стовпчиком”. Така схема у випадку чотирьохрозрядного множеного A = A₄A₃A₂A₁ і двохрозрядного множника B = B₂B₁. має вигляд:

A₄ A₃ A₂ A₁



B₂ B₁

A₄B₁ A₃B₁ A₂B₁ A₁B₁

+

A₄B₂ A₃B₂ A₂B₂ A₁B₂

M₆ M₅ M₄ M₃ M₂ M₁

Звідкіля для значень розрядів добутку M_і (і = 1, 2,...,6) випливають наступні співвідношення:

, (7.47)

де знаком „+” позначена арифметична операція складання, а P₁  P₄ значення перенесень, що виникають при додаванні розрядів часткових добутків.

Оскільки однорозрядні арифметичні добутки A_iB_i, як показано вище, можна отримати за допомогою логічних елементів 2І, для побудови матричного помножувача згідно (7.47) потрібно вісім таких елементів. З співвідношення (7.47) також випливає, що для порозрядного складання добутків A_iB_i для отримання добутку багаторозрядних чисел A і B потрібен чотирьохрозрядний двійковий суматор, у схемі якого формуються і враховуються внутрішні перенесення P₁  P₄ (див. підрозділ 7.3.3). Схема матричного помножувача показана на рис. 7.44.

Рис. 7.44. Схема матричного

помножувача двійкових чисел

На виході схеми формується двійкове число M₆M₅M₄M₃M₂M₁ у беззнаковому форматі, яке є добутком чотирьохзначного A₄A₃A₂A₁ і двохзначного B₂B₁ чисел у такому ж форматі. Час виконання операції множення t_M складає

t_M = t_{зп кон} + t_, (7.48)

де t_{зп кон} – час затримки поширення сигналу кон’юнктора, t_  час виконання операції додавання суматором. Матричні помножувачі мають високу швидкодію і виконують операцію множення за один такт, що вигідно відрізняє їх від арифметичних блоків множення мікропроцесорів перших поколінь, які виконували цю операцію мікропрограмним способом за декілька тактів, шляхом виконання послідовності операцій додавання і зсуву.

7.3.7. Цифрові компаратори. Ці комбінаційні цифрові вузли призначені для порівняння двох двійкових чисел (слів). Їх назва походить від англійської compare – порівнювати. Результат порівняння чисел, який реалізує компаратор, можна представити у вигляді функції F, що приймає одиничне значення при виконанні умови, яка указана в її індексі. Наприклад, функція F_A=B дорівнює одиниці коли A = B і приймає нульове значення при A ≠ B. У загальному випадку компаратори мають три виходи, на яких реалізуються три булеві функції: F_A=B – рівність чисел, F_A>B – число A більше за B, F_A<B – число A менше за число B.

_Ai

Bi	Ei	Li
0 0 1 1	0 1 0 1	1 0 0 1	0 1 0 0

Рис. 7.45. Таблиця справжності функцій порівняння однорозрядних чисел „на рівність” E_i та „на менше” L_i

Компаратори багаторозрядних двійкових чисел A = A_nA_n-1…A_i…A₂A₁ і B = B_nB_n-1…B_i…B₂B₁ можна побудувати на основі елементарних цифрових вузлів, що виконують операцію порівняння однорозрядних двійкових чисел A_i і B_i. Для визначення логічної схеми таких елементарних компараторів введемо функцію порівняння однорозрядних чисел „на рівність” E_i та „на менше” L_i. Таблиця справжності для цих функцій показана на рис. 7.45.

З таблиці справжності випливає, що E_i є булевою функцією еквівалентності (див. підрозділ 4.1), яка описується логічним рівнянням:

E_i = = = = . (7.49)

Цю функцію реалізує логічний елемент еквівалентності, умовне графічне зображення якого наведено в табл. 4.1.

З таблиці справжності (рис. 7.45) випливає, що функція порівняння „на менше” L_і описується рівнянням

L_i = . (7.50)

На підставі співвідношень (7.49) і (7.50) можна побудувати схему компаратора однорозрядних двійкових чисел, яка наведена на рис. 7.46.

Порівняння багаторозрядних двійкових чисел A = A_nA_n-1…A_i…A₂A₁ і B = B_nB_n-1…B_i…B₂B₁ виконують шляхом порозрядного порівняння значень їх бітів A_i і B_i. Для цієї мети використовують схеми однорозрядних компараторів (рис. 7.46). Очевидно, рівність чисел A і B буде мати місце, тобто F_A=B = 1, у випадку, коли значення всіх однойменних розрядів цих чисел A_i і B_i співпадають, тобто E_i = 1 для всіх розрядів чисел i = 1, 2, ..., n. З урахуванням означеного, функція F_A=B є кон’юнкцією елементарних функцій порівняння „на рівність” E_i, тобто F_A=B = E_nE_n-1…E_i…E₂E₁. Останнє співвідношення на підставі закону де Моргана запишемо у вигляді:

F_A=B= = . (7.51)

Рис. 7.46. Схема порівняння однорозрядних чисел

„на рівність” та „на менше”

Порівняння багаторозрядних чисел A і B „на менше” починають з їх старших розрядів A_n та B_n. Очевидно, A буде менше за B, якщо однорозрядна функція порівняння старших розрядів „на менше” дорівнює одиниці L_n = 1. У випадку коли A_n = B_n, число A менше за B при умові, що кон’юнкція E_nL_n-1 = 1. При рівності розрядів A_n = B_n і A_n-1 = B_n-1 виконання умови A < B забезпечується, коли кон’юнкція E_nE_n-1L_n-2 = 1 і так далі. Таким чином, якщо узагальнити всі випадки виконання умови, при якій A < B, то функцію порівняння багаторозрядних двійкових чисел A = A_nA_n-1…A_i…A₂A₁ і B = B_nB_n-1…B_i…B₂B₁ „на менше” F_A<B можна записати як диз’юнкцію кон’юнкцій однорозрядних функцій порівняння „на рівність” E_i та „на менше” L_і у наступному вигляді:

F_A<B=L_n + E_nL_n-1 + … + E_nE_n-1…E_i+1L_i + … + E_nE_n-1…E₂L₁.

На підставі закону де Моргана перетворимо це співвідношення до вигляду:

F_A<B= =

= . (7.52)

У співвідношеннях (7.51) і (7.52) стоять інверсні значення функцій E_i і L_i. Це дає можливість спростити схему компаратора однорозрядних чисел, наведену на рис. 7.46 при її використанні в компараторах багаторозрядних двійкових чисел. З неї можна вилучити елемент DD3, а елемент 2І DD6 замінити на логічний елемент 2ІНЕ.

З (7.51) та (7.52) також випливає, що при зростанні розрядності n зростає кількість входів логічних елементів ІНЕ, АБО в схемі багаторозрядного компаратора. Тому компаратори, звичайно, будують з розрядністю не більше чотирьох, а при потребі створення компараторів на більшу розрядність, їх нарощують шляхом використання декількох компараторів з меншою розрядністю. Для нарощування розрядності в компараторах створюють спеціальні входи, до яких при нарощуванні підключаються виходи F_A>B, F_A=B, F_A<B компаратора сусідніх молодших розрядів. Позначимо логічні змінні, що діють на входах нарощування, як , , . Вони задають результат порівняння молодших розрядів багаторозрядних чисел, який можна врахувати у співвідношеннях (7.51), (7.52) таким чином:

F_A=B = ; (7.53)

F_A<B = . (7.54)

Функцію виходу компаратора F_A>B можна визначити на підставі функцій F_A=B, F_A<B. Очевидно, F_A>B =1, коли F_A=B = F_A<B =0. Це свідчить про те, що булеву функцію F_A>B можна визначити, як заперечення диз’юнкції булевих змінних F_A=B, F_A<B, тобто

F_A>B = . (7.55)

Схему компаратора, яку можна побудувати на підставі співвідношень (7.53)  (7.55), розглянемо на прикладі компаратора чотирьохрозрядних двійкових чисел. Логічні рівняння (7.53)  (7.54) у випадку чотирьохрозрядного компаратора приймають вигляд

F_A=B = ;

F_A<B = .

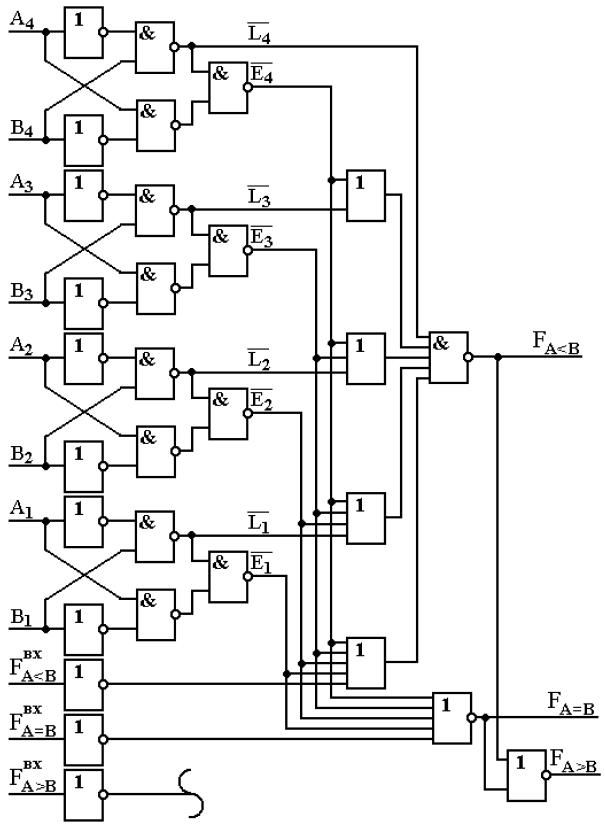
З них і співвідношення (7.55) випливає, що для побудови компаратора чотирьохрозрядних двійкових чисел потрібно чотири схеми однорозрядних компараторів (рис. 7.46), модифікованих з урахуванням інверсних значень функцій однорозрядного порівняння E_i і L_i, два інвертори, а також логічні елементи 2АБОНЕ, 5АБОНЕ, 5ІНЕ, 2АБО, 3АБО, 4АБО і 5 АБО. Схема чотирьохрозрядного компаратора двійкових чисел показана на рис. 7.47.

Зазначимо, що в цій схемі вхід нікуди не підключено, оскільки функція виходу компаратора F_A>B згідно співвідношенню (7.55) реалізується як заборона диз’юнкції вихідних функцій F_A=B і F_A<B логічним елементом 2АБОНЕ.

Рис. 7.47. Схема чотирьохрозрядного компаратора

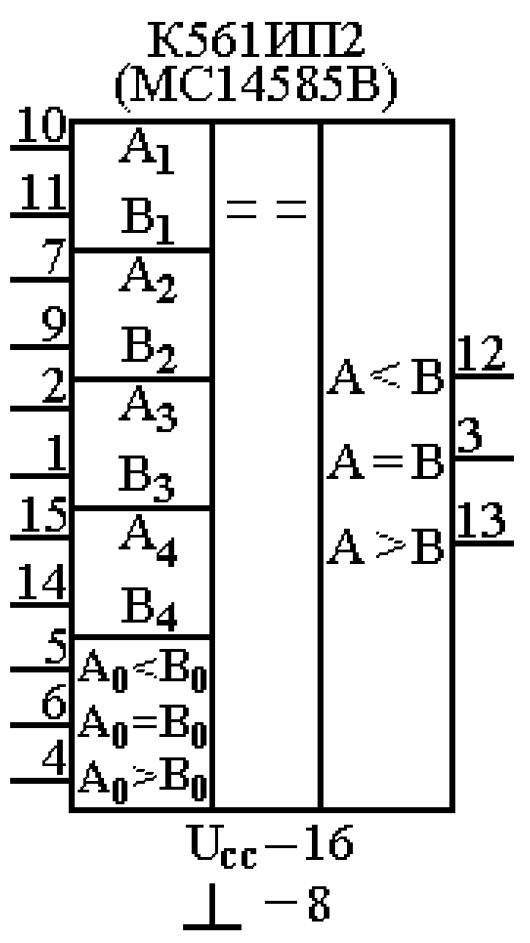
Прикладом компаратора, реалізованого за схемою показаною на рис. 7.47, є мікросхема К561ИП2 (функціональний аналог MC14585B). Її умовне графічне зображення і нумерація виводів показані на рис. 7.48а.

а	б
Рис. 7. 48. Умовне графічне зображення мікросхеми К561ИП2 (а), нарощування розрядності компараторів (б)

В табл. 7.8. наведені параметри мікросхеми К561ИП2 при температурі 25 ^оС

Таблиця 7.8

Параметри інтегральної мікросхеми

компаратора К561ИП2

Позначення параметра	Параметр	Значення	Одиниця виміру
Ucc	Напруга живлення	2 – 18	В
Icc	Струм споживання у стані спокою	600 (15 В)	мкА
TA	Робочий діапазон температури	55 – +125	^оС
U^0вих (UOL)	Вихідна напруга логічного нуля	≤0,5 (5 В) ≤0,5 (15 В)	В
U^1вих (UOH)	Вихідна напруга логічної одиниці	4,95 (5 В) 14,95 (15 В)	В
Iвх, Iin	Вхідний струм	0,1	мкА
I^0вих (IОL)	Вихідний струм низького рівня	0,88 (5 В) 8,8 (15 В)	мА
I^1вих (IОH)	Вихідний струм високого рівня	0,88 (5 В) 8,8 (15 В)	мА
tзп^1,0 (tPHL), tзп^0,1 (tPLH)	Час затримки поширення сигналу	430 (5 В) 130 (15 В)	нс
tвм^1,0(tTHL), tвим^0,1(tTLH)	Час вмикання і вимикання	100 (5 В) 40 (15 В)	нс

Для нарощування розрядності компараторів їх вмикають так, як показано на рис. 7.48б. Виходи A<B, A=B, A>B компараторів молодших розрядів з’єднують з відповідними входами A₀<B₀, A₀=B₀, A₀>B₀ компараторів сусідніх старших розрядів. При цьому на входи нарощування A₀<B₀, A₀=B₀, A₀>B₀ компаратора самих молодших розрядів треба подати напругу низького рівня U⁰ (логічний „0”), тобто підключити їх до землі (рис. 7.48б).

7.3.8. Використання двійкових суматорів для порівняння чисел. Компаратори, що виконують порівняння чисел „на рівність та менше” (F_A≤B) і „на більше” (F_A>B) можуть бути побудовані на основі двійкових суматорів. Розглянемо принципи створення таких компараторів на прикладі чотирьохрозрядних цілих чисел A = A₄A₃A₂A₁ і B = B₄B₃B₂B₁, представлених в беззнаковому форматі з фіксованою крапкою (всі біти A_i, B_i є цифровими).

Нехай A < B, наприклад, A = 5₁₀ = 0101₂, а число B = 13₁₀ = 1101₂. Виконаємо операцію віднімання A – B шляхом додавання до зменшуваного A від’ємника B, представленого у оберненому коді (без врахування циклічного перенесення):

.

Як видно, при виконанні операції складання перенесення зі старшого біта результату дорівнює нулю P = 0. Нескладно переконатися, що P = 0 також при умові A = B.

Нехай тепер A > B, наприклад, A = 7₁₀ = 0111₂, а число B = 5₁₀ = 0101₂. Тоді при виконанні операції A – B означеним вище шляхом

виникає перенесення P = 1.

Таким чином, виникнення перенесення зі старшого біта результату при складанні числа A з оберненим кодом числа B (P = 1) свідчить про виконання умови A > B і, навпаки, коли таке перенесення відсутнє (P = 0) – про виконання умови A ≤ В. Тому суматор, на входи якого число B подається через інвертори, може виконувати функцію порівняння двійкових чисел. Результат порівняння формується на виході перенесення суматора P. Схема чотирьохрозрядного компаратора на суматорі, який виконує порівняння цілих двійкових чисел у беззнаковому форматі з фіксованою крапкою „на більше” і „на рівність та менше” показана на рис. 7.49.

Рис. 7.49. Використання суматора для порівняння цілих двійкових чисел, що представлені у

беззнаковому форматі

Відзначимо також, що коли суматор виконує арифметичну операцію, наприклад, увімкнений за схемою на рис. 7.41а для виконання операції віднімання чисел A і B у оберненому коді, то він не тільки формує результат операції на виходах S_i, але сигнал на його виході перенесення P є ознакою порівняння чисел. Таку ознаку називають ознакою результату. Ознаки результату мають важливе значення для управління обчислювальним процесом у комп’ютері, зокрема, при виконанні команд умовних переходів. Ознаку результату формують всі арифметичні і деякі логічні команди, що входять до системи команд процесора. Ці ознаки фіксують спеціальні керуючі тригери, що входять до складу процесора. Сукупність таких тригерів складає так званий регістр прапорів. Інформація, що зберігається в цьому регістрі, використовується для керування обчислювальним процесом.