
- •Предисловие
- •Занятие 1.Понятие функции, предела и непрерывности функции. Производная функции
- •Краткие сведения из теоретического курса Понятие функции
- •Определение предела функции и бесконечно малой функции
- •Основные теоремы о пределах
- •Производная функции
- •Производная сложной функции
- •Занятие 2.Дифференциал функции. Производные и дифференциалы высших порядков. Применение производных к решению прикладных задач
- •Дифференциал функции
- •Геометрический смысл дифференциала функции
- •Производные высших порядков
- •Механический смысл производной второго порядка
- •Дифференциалы высших порядков
- •Приложение дифференциального исчисления
- •Производные и дифференциалы функции нескольких аргументов
- •Основные понятия
- •Частные производные и дифференциалы функции нескольких переменных
- •Полный дифференциал функции
- •Частные производные второго порядка
- •Решение задач
- •Неопределенный интеграл и его основные свойства. Основные методы интегрирования.
- •Основные понятия
- •Свойства неопределенного интеграла
- •Метод непосредственного интегрирования
- •Метод замены переменной (подстановки)
- •Метод интегрирования по частям
- •6. Задание на дом.
- •Определенный интеграл и его основные свойства. Приложения определенного интеграла.
- •Определенный интеграл как предел интегральной суммы
- •Свойства определенного интеграла
- •Геометрический смысл определенного интеграла
- •Формула Ньютона-Лейбница
- •Метод замены переменных в определенном интеграле
- •Метод интегрирования по частям в определенном интеграле
- •Задача о площади криволинейной трапеции
- •Работа переменной силы
- •Занятие 3.Основные понятия теории вероятностей. Классическое и статистическое определение вероятности. Круглый стол «Применение математического анализа при решении задач физики, химии, фармации»
- •Понятие испытания, события, виды событий
- •Свойства вероятности:
- •Самостоятельная работа студентов на занятии
- •Занятие 4.Теорема сложения вероятностей для несовместных событий. Случайные величины. Числовые характеристики дискретной случайной величины
- •Теорема сложения независимых событий
- •Случайные величины
- •Закон распределения дискретной случайной величины
- •Числовые характеристики случайной величины
- •Дисперсия дискретной случайной величины
- •Среднее квадратическое отклонение
- •Функция распределения случайной величины
- •График функции распределения
- •Плотность распределения вероятностей. Дифференциальная функция распределения
- •Свойства плотности распределения
- •Характеристики непрерывных случайных величин
- •Нормальное распределение
- •Влияние параметров нормального распределения на форму нормальной кривой
- •Вероятность попадания в заданный интервал нормальной случайной величины
- •Занятие 6.Статистическое распределение выборки, дискретные и интервальные вариационные ряды. Точечные оценки параметров распределения. Доверительный интервал и доверительная вероятность.
- •Генеральная и выборочная совокупности
- •Статистический дискретный ряд распределения
- •Статистический интервальный ряд распределения
- •Полигон и гистограмма
- •Эмпирическая функция распределения
- •Оценки характеристик распределения
- •Оценка математического ожидания
- •Оценка дисперсии
- •Оценка среднего квадратического отклонения
- •Интервальные оценки
- •2. Результаты наблюдений за числом частиц, попавших в счетчик Гейгера в течение минуты, приведены в виде интервального ряда распределения:
- •Построим гистограмму (рис. 9.4)
- •3. Найти оценку математического ожидания и несмещенную оценку дисперсии, если дана таблица распределения:
- •Решение. Для вычисления характеристик воспользуемся расчетной таблицей:
- •Самостоятельная работа студентов на занятии
- •Занятие 7.Погрешности измерений и их оценки. Погрешности прямых и косвенных измерений
- •Погрешности измерений. Истинная, абсолютная и относительные погрешности
- •Типы погрешностей
- •Оценка истинного значения измеряемой величины
- •Вычисление абсолютной погрешности косвенных измерений
- •Занятие 8.Контрольная работа
- •Занятие 9.Деловая игра «Статистика знает все»
- •Приложения
- •I. Греческий алфавит
- •II. Некоторые постоянные
- •III. Обратные величины, степени, корни, логарифмы
- •IV. Значение функции ех и е -х
- •V. Тригонометрия Значения тригонометрических функций
- •Критические значения распределения Стьюдента
- •Значения функции и
- •Библиографический список
- •Практикум по математике
Занятие 1.Понятие функции, предела и непрерывности функции. Производная функции
Актуальность темы: Предел функции используется в определении многих математических понятий, например, производной функции одного аргумента, производной функции нескольких переменных, непрерывности функции, определенного интеграла и т. д. Понятие производной является одним из основных математических понятий. Производная широко используется при изучении скорости разных процессов
Цель занятия: Выработать навыки нахождения пределов функций одной переменной и закрепить навык нахождения производных функций одной переменной, производных сложных функций.
Целевые задачи:
знать: понятия предела функции, понятие бесконечно малой функции, основные теоремы о пределах; понятия приращения аргумента и функции, понятие производной функции, ее геометрический и механический смысл, производную сложной функции, основные правила дифференцирования и таблицу производных;
уметь: находить простейшие пределы; применять основные правила дифференцирования и таблицу производных при решении примеров, находить производные сложных функций.
Краткие сведения из теоретического курса Понятие функции
Одним из основных математических понятий является понятие функции.
Пусть даны два непустых множества Х и У. Соответствие f, которое каждому элементу х Х сопоставляет один и только один элемент у У, называется функцией и записывается у =f(x), или х Х: Х У. Говорят еще, что функция f отображает множество Х на множество У.
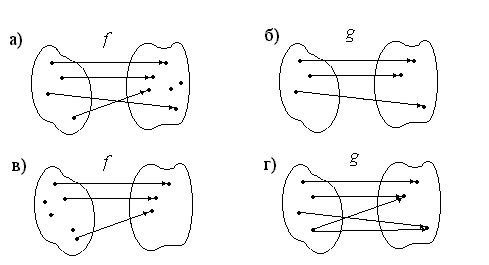
Рис. 1.1. Примеры соответствий между множествами
Например, соответствия f и g, изображенные на рисунках а) и б), являются функциями, а на рисунках в) и г) – нет. В случае в) – не каждому элементу х Х соответствует элемент у У. В случае г) не соблюдается условие однозначности.
Множество Х называется областью определения функции f и обозначается D(f). Множество всех у У называется множеством значений функции f и обозначается Е(f).
Определение предела функции и бесконечно малой функции
Пусть функция у=f(x) определена в некоторой окрестности точки х0, кроме, может быть, самой точки х0.
Определение:
Число А
называется
пределом функции в точке х0
(или при
х
х0),
если для любого положительного
найдется такое положительное число ,
что для всех хх0,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
Записывается
предел функции в точке следующим
образом:
![]() .
.
Геометрически смысл предела функции: , если для любой ε–окрестности точки А найдется такая этой δ – окрестность точки х0, что для всех х х0 из этой δ – окрестности соответствующие значения функции f(x) лежат в ε–окрестности точки А. То есть, точки графика функции y=f(x) лежат внутри полосы шириной 2, ограниченной прямыми у =А+, у =А–. Величина зависит от выбора (рис. 1.2).
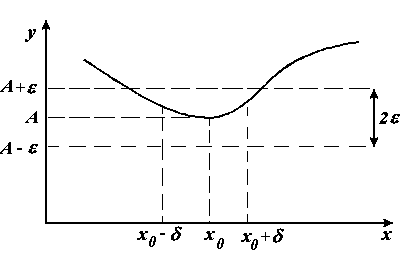
Рис. 1.2. К понятию предела функции
Определение:
Функция y=f(x) называется бесконечно
малой
при х
х0,
если
![]() .
.
Обозначают бесконечно малые функции греческими буквами или хх и т. д.
Теорема (о связи бесконечно малой функции и предела). Если функция f(x) при х х0 имеет предел, равный числу А, то она может быть представлена в виде f(x)= A + (x), где (x) – бесконечно малая.
Справедливо и
обратное утверждение:
Если функцию f(x)
можно представить в виде суммы числа
А и бесконечно малой функции
![]() ,
то число А
является пределом функции
f(x)
при х
х0.
,
то число А
является пределом функции
f(x)
при х
х0.
