Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции, т. е. .

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. .

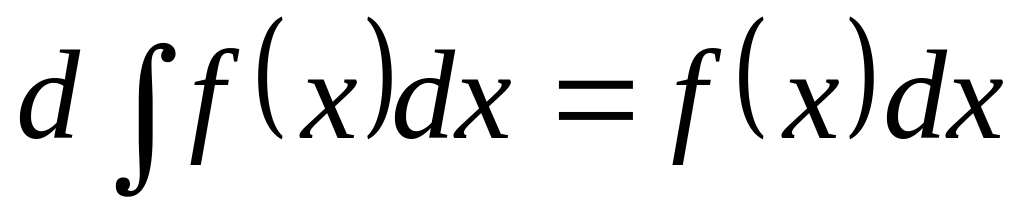3. Интеграл от дифференциала первообразной равен самой первообразной и дополнительному слагаемому С, т. е.

4. Постоянный множитель не равный нулю можно вынести за знак неопределенного интеграла, т. е.

5. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых, т. е.

.

Таблица простейших интегралов

1. ;

2. ;

3. , при ;

4. , ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

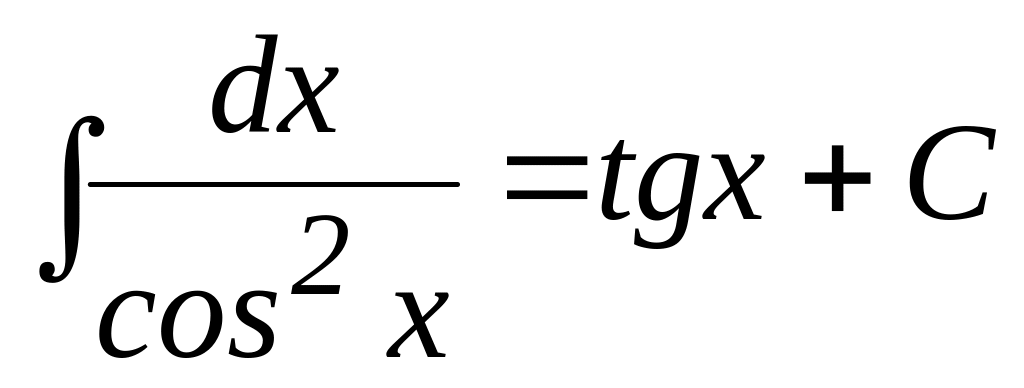Метод непосредственного интегрирования

Метод непосредственного интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и использовании свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Метод замены переменной (подстановки)

Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к табличному виду. В интеграле сделаем подстановку , где функция имеет непрерывную производную. Тогда: на основании независимости неопределенного интеграла от выбора аргумента: – формула замены переменных в неопределенном интеграле. Иногда целесообразно подбирать подстановку в виде , тогда , где .

Метод интегрирования по частям

Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей u и dv (это, как правило, можно осуществить несколькими способами); затем, после нахождения v и du, используется формула интегрирования по частям.

Если u=u(x) и v=v(x) – дифференцируемые функции, тогда d(uv)=vdu+udv, откуда udv=d(uv)-vdu. Интегрируя последнее выражение, получаем: – формула интегрирования по частям, которая применяется в тех случаях, если интеграл в правой части более прост, чем исходный. Эта формула дает возможность свести вычисление интеграла к вычислению интеграла , который может оказаться существенно более простым, чем исходный.

Решение задач

Пример 7.1. Найти интегралы:

1) . 2) .

Решение. 1) Применяя свойства 4 и 5 неопределенного интеграла, а также алгебраические преобразования сведем интеграл к трем табличным интегралам:

;

2) Учитывая, что и используя основные формулы интегрирования, имеем: .

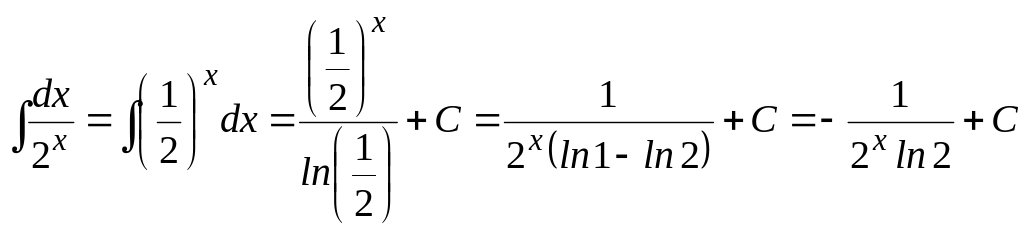Пример 7.3. Найти интегралы:

1) . 2) .

Решение. 1) Введем замену: пусть x=4t, тогда dx=d(4t)=4dt. Следовательно, можем записать:

.

2) Положим . Тогда , следовательно . Можем записать:

.

Пример 7.4. Найти интеграл .

Решение. Интеграл будем искать методом интегрирования по частям. Положим , ; тогда , . Применяем формулу интегрирования по частям: .

Мы добились понижения степени х на единицу. Чтобы найти , применим ещё раз интегрирование по частям. Пусть , ; тогда , и можно записать

.

Пример 7.5. Найти интегралы:

1) .

2)  .

3) .

4 ;

5)  .

Решение: 1). Применим метод непосредственного интегрирования:

2). Воспользуемся формулой сокращенного умножения для преобразования подынтегральной функции и применим метод непосредственного интегрирования:

.

3). Этот интеграл можно найти с помощью замены переменной. Полагая , имеем , т.е. . Отсюда получим

.

4). Введем подстановку:

5). Применим метод интегрирования по частям. Пусть ; тогда . Используя формулу интегрирования по частям, получим .

Пример 7.6. Найти закон изменения скорости тела, если уравнение ускорения имеет вид: и, если известно, что скорость тела через 2 секунды была равна 10 .

Решение: Так как ускорение движения тела есть первая производная скорости движения по времени, то имеет место формула . Следовательно, можно записать . Проинтегрировав данное соотношение, получим . Тогда .

Исходя из начальных условий: при , найдем С:

 .

Итак, уравнение скорости движения тела .

Самостоятельная работа студентов на занятии.

Найти интегралы

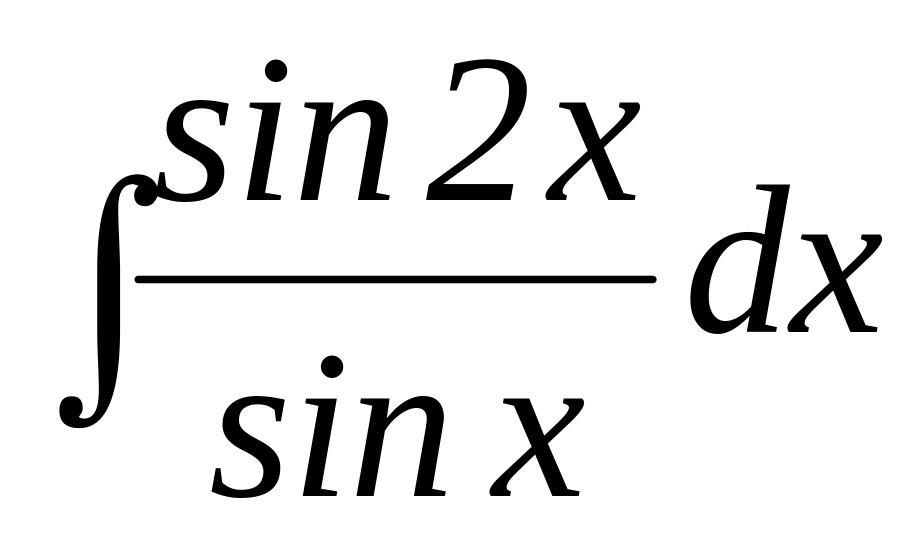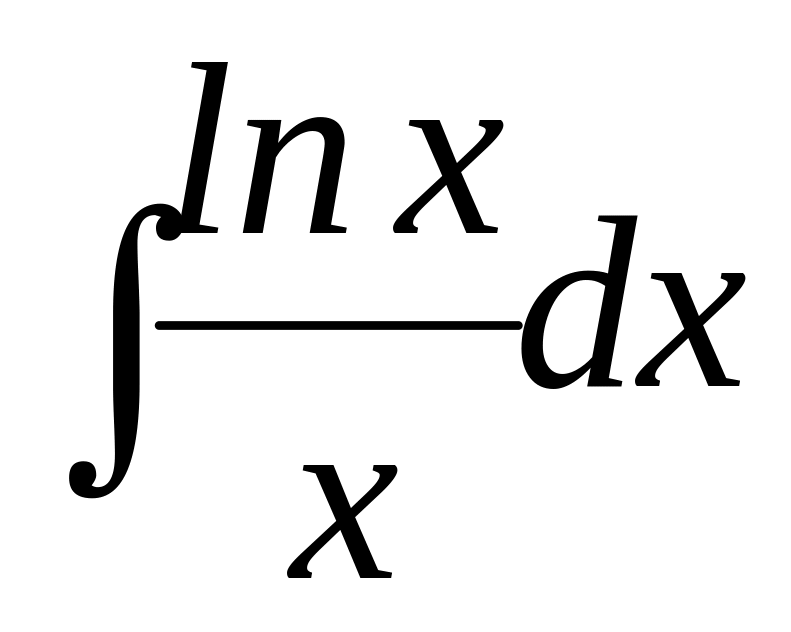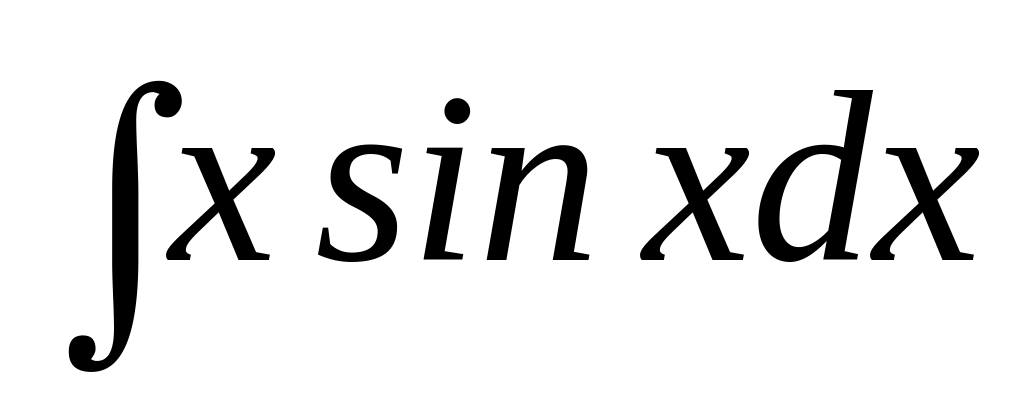1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .