§6 Диференціальні рівНянНя

Література: [1] – ст. 614-657; [2] – ст. 352-368; [3] – ст. 315-345; [4] – ст. 421-473.

Означення. Рівняння, які пов’язують незалежну змінну , шукану функцію та її похідні або диференціали називають диференціальними рівняннями.

Означення. Порядком диференціального рівняння називають найвищий порядок похідної або диференціала від шуканої функції, яка входить у це рівняння.

В загальному вигляді диференціальне рівняння порядку подається так

(6.1)

або

(6.2)

Диференціальне рівняння першого порядку має вигляд

(6.3)

або

(6.4)

Загальним розв’язком диференціального рівняння (6.4) в області , називається функція , яка в результаті підстановки в диференціальне рівняння перетворює його в тотожність по при будь-яких допустимих значеннях сталої .

Частинним розв’язком називається будь-який розв’язок , який одержується із загального розв’язку при певному значенні сталої .

Задачею Коші називається задача знаходження частинного розв’язку диференціального рівняння (6.4), що задовольняє умову .

Умова називається початковою умовою диференціального рівняння.

6.1 Диференціальні рівняння і порядку Диференціальні рівняння з відокремлюваними змінними.

Рівняння виду

називається рівнянням з відокремлюваними змінними.

Рівняння розв’язується шляхом відокремлення змінних. Для відокремлення змінних поділимо рівняння на функцію і дістанемо диференціальне рівняння з відокремленими змінними

(припускаємо, що ).

Якщо і , то також розв’язки диференціального рівняння (особливі розв’язки). Проінтегруємо обидві частини рівняння

.

Зразки розв’язування задач

Приклад 1 (Задача 4.1 (а))

Знайти загальний розв’язок диференціального рівняння

.

Розв’язання.

Запишемо рівняння у вигляді:

.

Поділимо обидві частини на і помножимо на

Інтегруємо обидві частини рівняння

– загальний розв’язок диференціального рівняння (загальний інтеграл).

Відповідь: .

Однорідні диференціальні рівняння

Означення. Функція називається однорідною виміру відносно змінних і , якщо для довільного значення виконується тотожність:

.

Означення. Диференціальне рівняння називається однорідним, якщо – однорідна функція нульового виміру.

Однорідне рівняння можна записати у вигляді

Однорідне рівняння можна звести до рівняння з відокремлюваними змінними підстановкою .

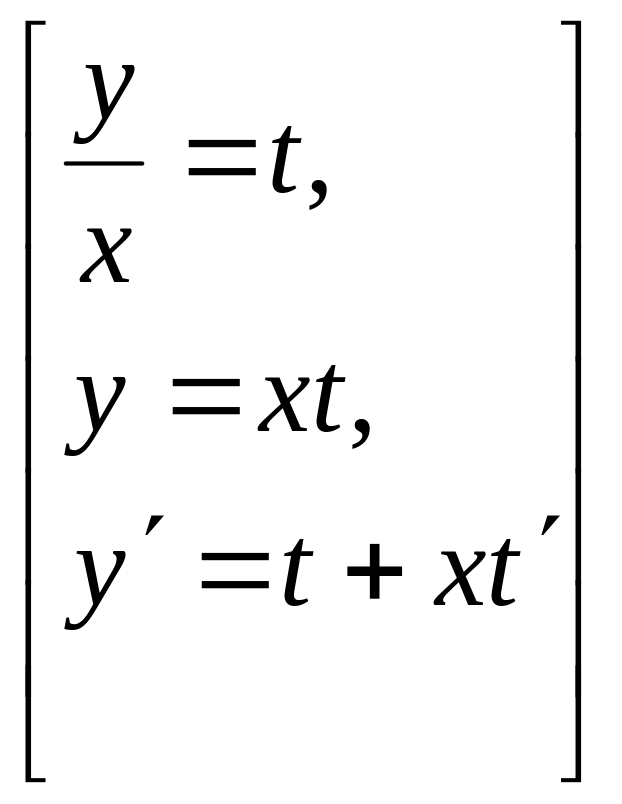Приклад 2 (Задача 4.1 (б)) Знайти загальний розв’язок диференціального рівняння .

Розв’язання.

Рівняння однорідне. Виконаємо підстановку . Рівняння набуде вигляду

.

Повертаючись до заміни одержимо

Відповідь: .

Зауваження. До однорідних відносяться також рівняння виду: , якщо – однорідні функції одного виміру. В цьому випадку зручно використати підстановку , .

Лінійні диференціальні рівняння

Означення. Рівняння називається лінійними диференціальним рівнянням.

Розв’яжемо рівняння методом Бернуллі.

Розв’язок рівняння шукають у вигляді , де – невідомі функції , причому одна з них довільна (але не рівна тотожно нулю).

Знаходимо похідну і підставляючи значення та в рівняння (1) дістанемо

Користуючись довільністю у виборі функції знайдемо її так, щоб тоді .

Тобто, розв’язавши сукупність рівнянь:

знайдемо функції .

Приклад 3. (Задача 4.1 (в)) Знайти загальний розв’язок рівняння .

Запишемо рівняння так .

Нехай , тоді

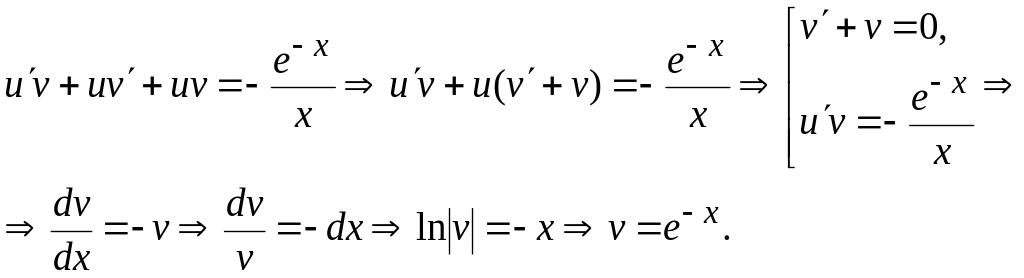
Отже, .

Відповідь: .