
- •Передмова
- •§1. Елементи лінійної алгебри і аналітичної геометрії
- •Елементи лінійної алгебри
- •Системи лінійних алгебраїчних рівнянь
- •Матриця
- •Матричний метод, правило Крамера
- •Зразки розв’язування задач
- •Контрольні запитання
- •1.2 Елементи аналітичної геометрії. Вектори та дії над ними
- •Мішаний добуток векторів.
- •Зразки розв’язування задач
- •Пряма на площині.
- •Контрольні запитання
- •Задачі контрольної роботи №1
- •§ 2. Введення в математичний аналіз. Границя функції
- •Зразки розв’язування задач
- •Контрольні запитання
- •§ 3. Диференціальне числення функції однієї змінної
- •Зразки розв’язування задач
- •Застосування диференціального числення для дослідження функцій
- •Застосування диференціального числення до економічних задач
- •Контрольні запитання
- •Як можна знайти найбільше й найменше значення функції на відрізку? Задачі контрольної роботи №2
- •§4 Диференціальне числення функцій багатьох змінних
- •Зразки розв’язування задач
- •Метод найменших квадратів можливої лінійної залежності між змінними
- •Контрольні запитання
- •§5 Інтегральне числення функції однієї змінної
- •5.1 Невизначений інтеграл
- •Основні методи інтегрування
- •Зразки розв’язування задач
- •5.2 Визначений інтеграл
- •Зразки розв’язування задач
- •5.3 Використання визначеного інтеграла в економіці
- •Зразки розв’язування задач
- •5.4 Невласні інтеграли першого роду
- •Зразки розв’язування задач
- •Контрольні запитання
- •Задачі контрольної роботи №3
- •§6 Диференціальні рівНянНя
- •6.1 Диференціальні рівняння і порядку Диференціальні рівняння з відокремлюваними змінними.
- •Зразки розв’язування задач
- •Однорідні диференціальні рівняння
- •Лінійні диференціальні рівняння
- •6.2 Диференціальні рівняння іі порядку Лінійні диференціальні рівняння іі порядку з сталими коефіцієнтами
- •Зразки розв’язування задач
- •Знаходження частинного розв’язку неоднорідного рівняння методом невизначених коефіцієнтів.
- •Контрольні запитання
- •§7 Ряди
- •Зразки розв’язування задач
- •Знакозмінні ряди
- •Степеневі ряди
- •Контрольні запитання
- •Задачі контрольної роботи №4
- •Література
Контрольні запитання
1 Що таке функція одного аргументу?
2 Що називають областю визначення функції?
3 Що називається областю значень функції?
4 Які основні способи задання функції?
5 Яку функцію називають монотонною, парною, непарною, періодичною?
6 Яку функцію називають складною?
7 Які функції належать до основних елементарних функцій?
8 Які функції називають елементарними?
9 Як формулюється означення границі функції в точці?
10 Які основні властивості функції, що має границю?
11 Яку функцію називають нескінченно малою, а яку – нескінченно великою? Який зв'язок між ними?
12 Які основні властивості нескінченно малих функцій?
13 Які нескінченно малі функції називають еквівалентними?
14 Як формулюються основні теореми про границі функцій?
15 Як визначають важливі границі?
16 Які існують типи невизначеностей?
§ 3. Диференціальне числення функції однієї змінної
Література: [1] – с. 279-390, [2] – с. 216-263, [4] – с. 191-283.
Похідна
функції в точці.
Похідною функції
![]() в точці
називається границя (якщо вона існує)
відношення приросту функції
в точці
називається границя (якщо вона існує)
відношення приросту функції
![]() до приросту аргументу
до приросту аргументу
![]() ,
коли приріст аргументу прямує до нуля,
тобто
,
коли приріст аргументу прямує до нуля,
тобто
![]()
Функція, яка має скінченну похідну в точці , називається диференційовною в цій точці.
Основні правила диференціювання.
Якщо
функції
![]() і
і
![]() диференційовні в точці
,
тоді в цій точці мають місце такі
співвідношення:
диференційовні в точці
,
тоді в цій точці мають місце такі
співвідношення:
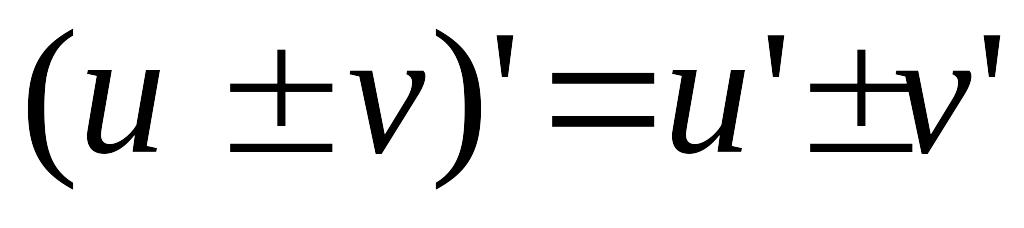 ;
;
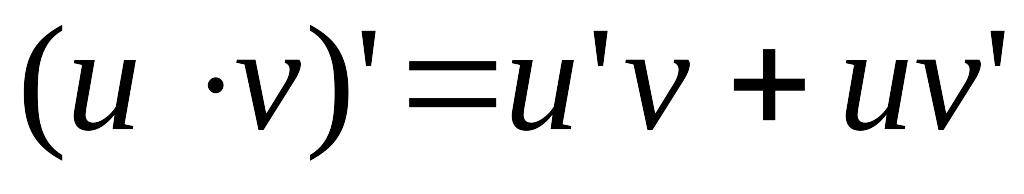 ;
;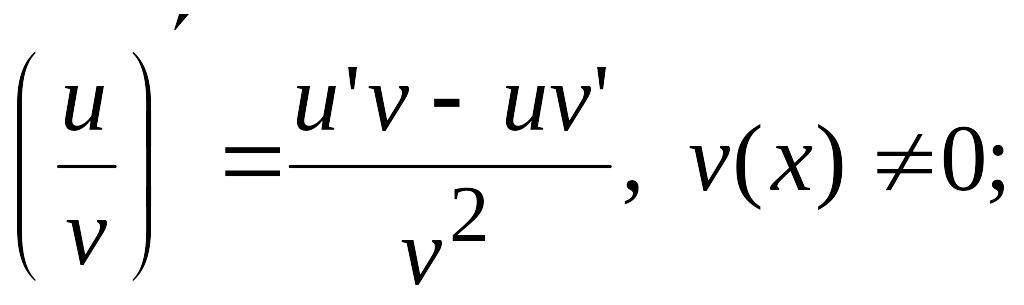
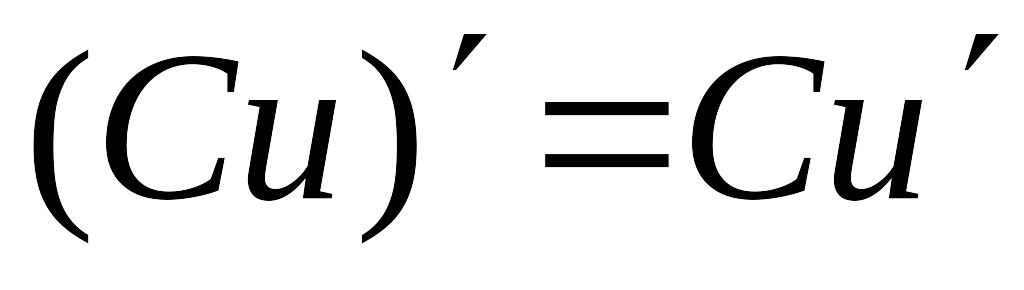 .
.
При розв’язанні задач на знаходження похідної застосовують ряд формул для похідних основних елементарних функцій:
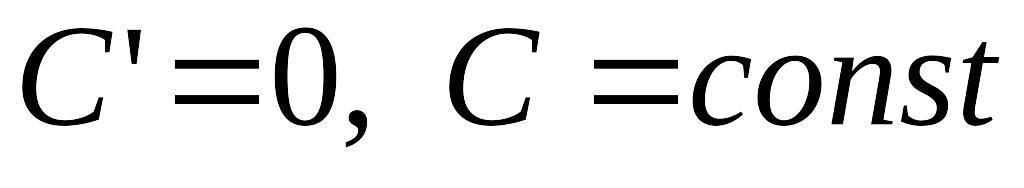 ;
;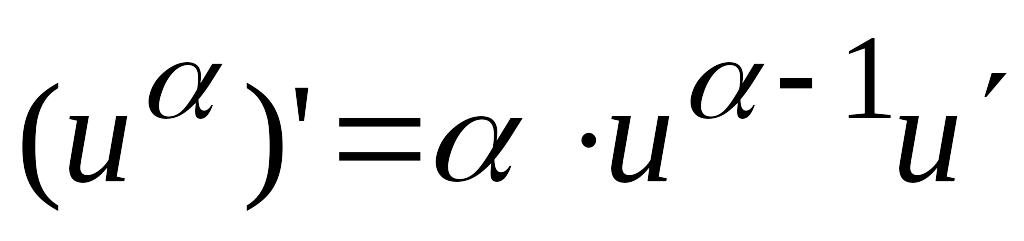 ,
(
,
( – довільне число);
– довільне число);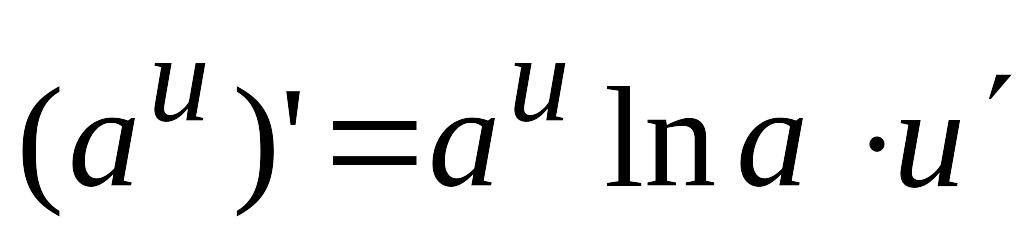 ,
(
,
( );
);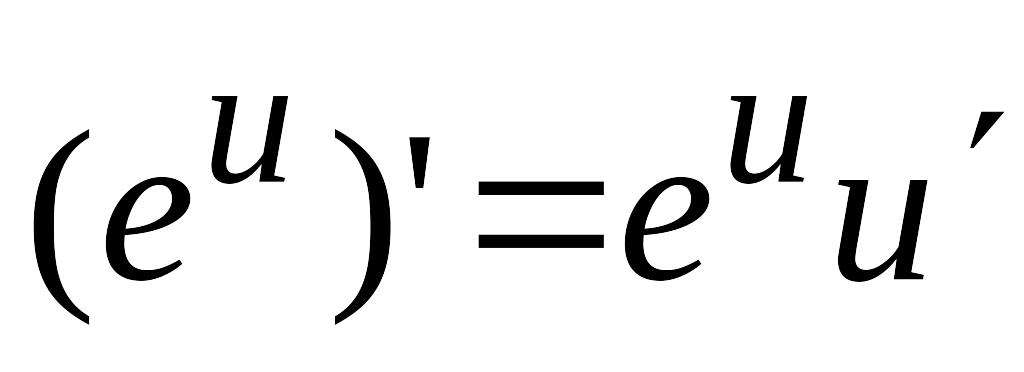 ;
;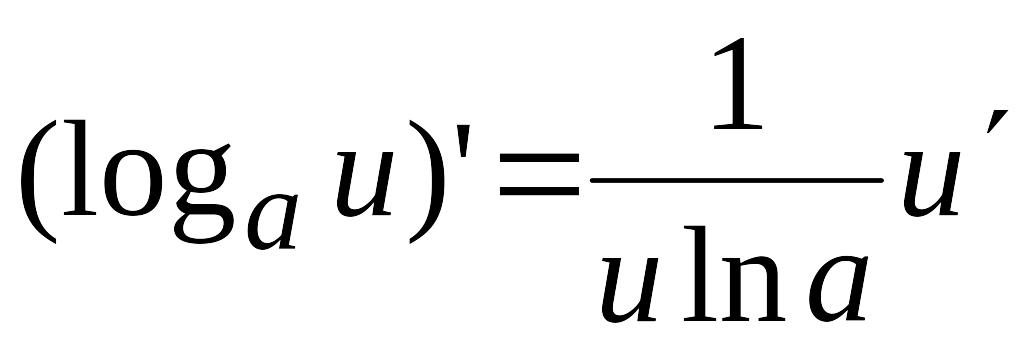 ;
;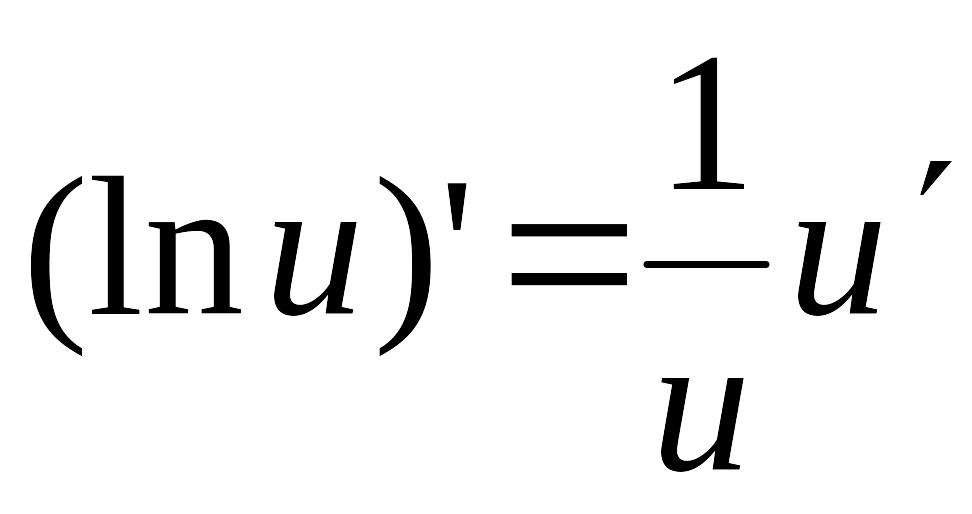 ;
; ;
;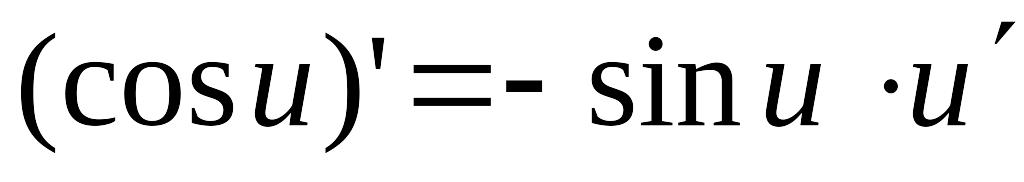 ;
;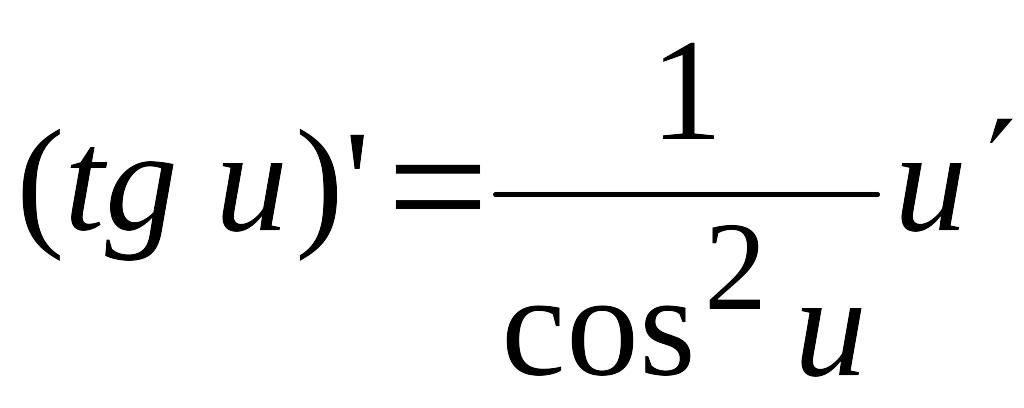 ;
;
10) 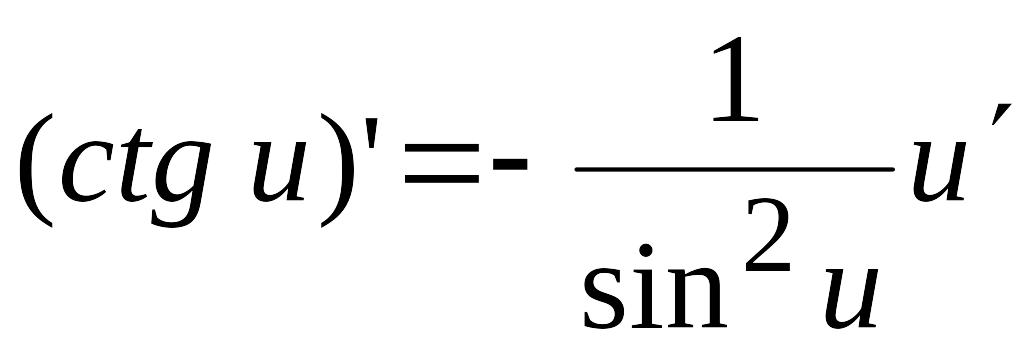 ;
;
11) 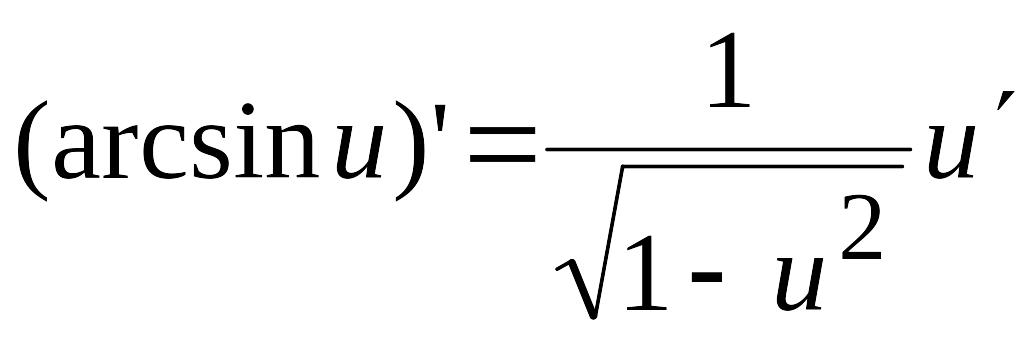 ;
;
12) 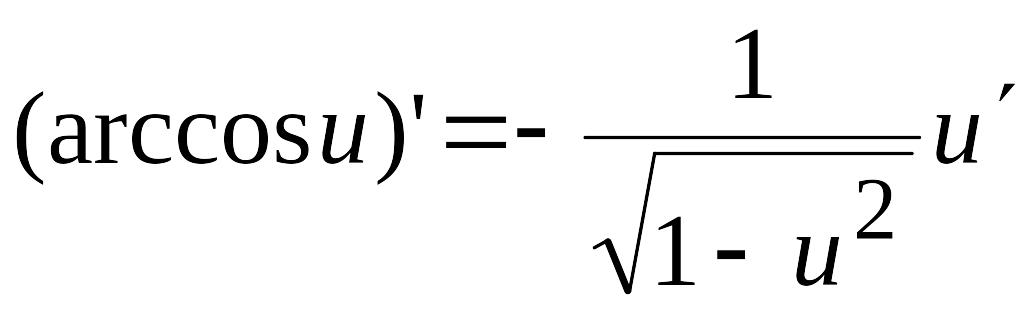
13) 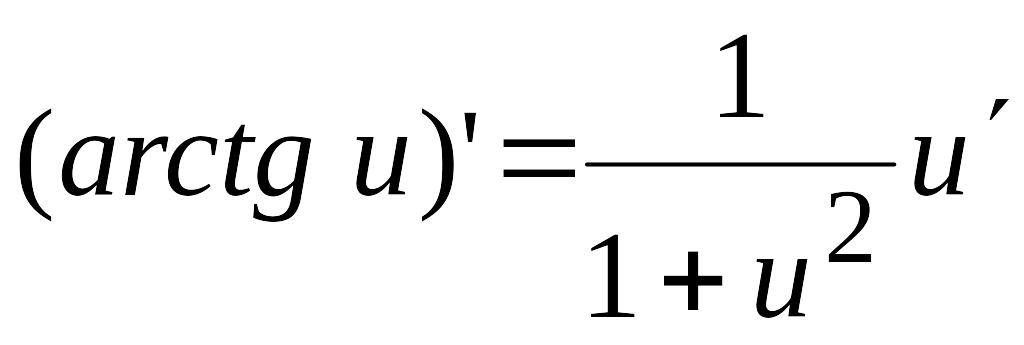 ;
;
14) 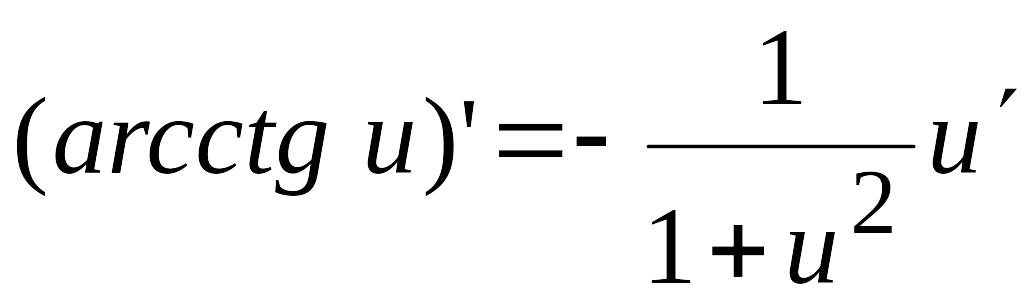 ;
;
15) ![]() ;
;
16) ![]() ;
;
17) 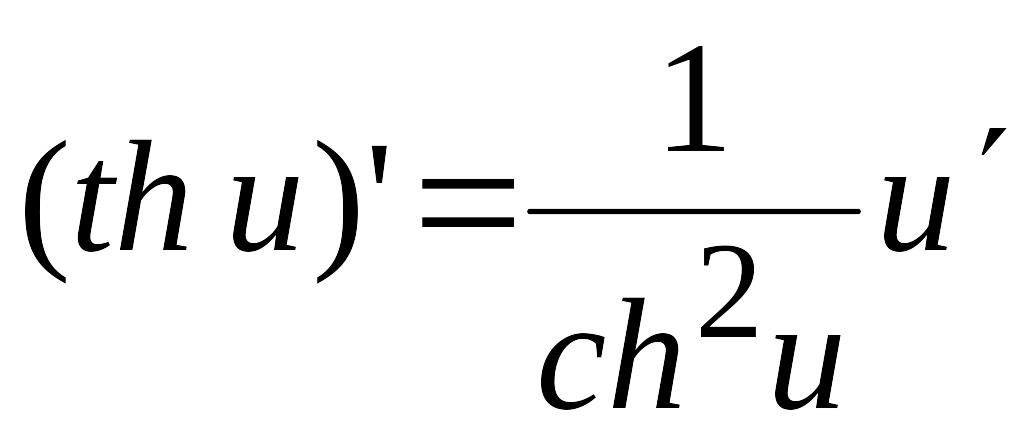 ;
;
18) 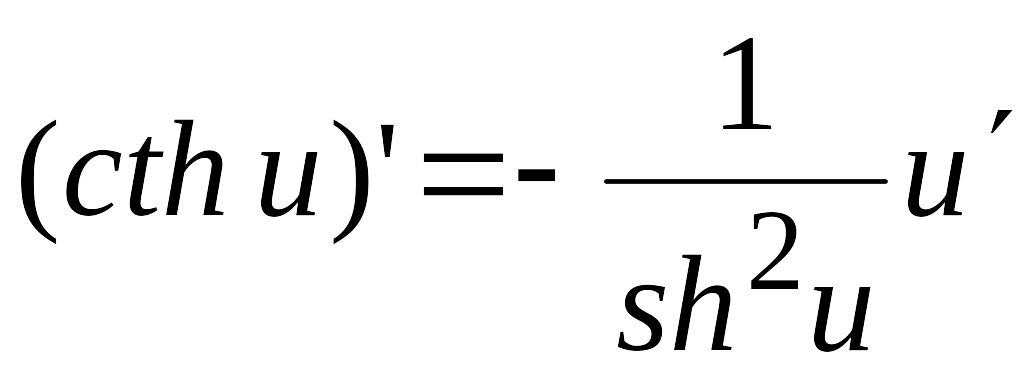 .
.
Похідна
складеної функції.
Якщо функція
![]() має похідну
має похідну
![]() в точці
,
а функція
в точці
,
а функція
![]() має похідну
має похідну
![]() у відповідній точці
у відповідній точці
![]() ,
то складена функція
,
то складена функція
![]() має похідну
має похідну
![]() в точці
і справедливою є формула
в точці
і справедливою є формула
![]() .
.
Похідна
функції, заданої параметрично.
Похідна функції, яка задана параметрично
рівняннями
![]() ,
де
,
де
![]() і
і
![]() диференційовні в точці
,
причому
диференційовні в точці
,
причому
![]() ,
обчислюється за формулою:
,
обчислюється за формулою:
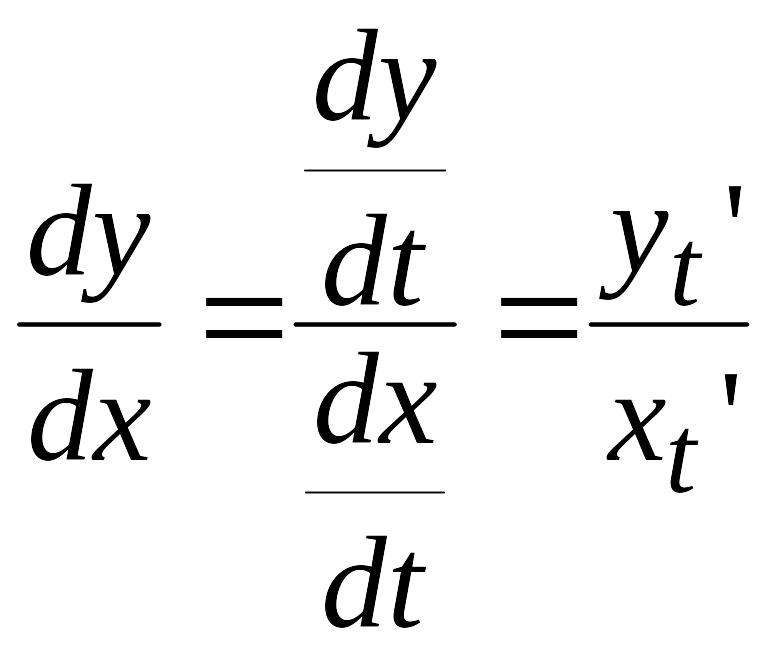 .
.
Диференціювання
неявної функції.
Нехай рівняння
![]() визначає
визначає
![]() як
неявну функцію від
.
Будемо вважати дану функцію диференційовною.
як
неявну функцію від
.
Будемо вважати дану функцію диференційовною.
Продиференціювавши
обидві частини рівняння
,
отримаємо рівняння першого степеня
відносно
![]() .
З цього рівняння легко знайти
,
тобто похідну неявної функції для всіх
значень
і
,
при яких множник
в рівнянні не перетворюється в нуль.
.
З цього рівняння легко знайти
,
тобто похідну неявної функції для всіх
значень
і
,
при яких множник
в рівнянні не перетворюється в нуль.
Диференціювання показниково-степеневої функції.
Похідну показниково-степеневої функції знаходять, провівши попереднє логарифмування.
![]() – показниково-степенева
функція,
– показниково-степенева
функція,
де
і
![]() – задані і диференційовні функції від
.
Маємо
– задані і диференційовні функції від
.
Маємо
![]() ,
,
![]() ,
,
 ;
;
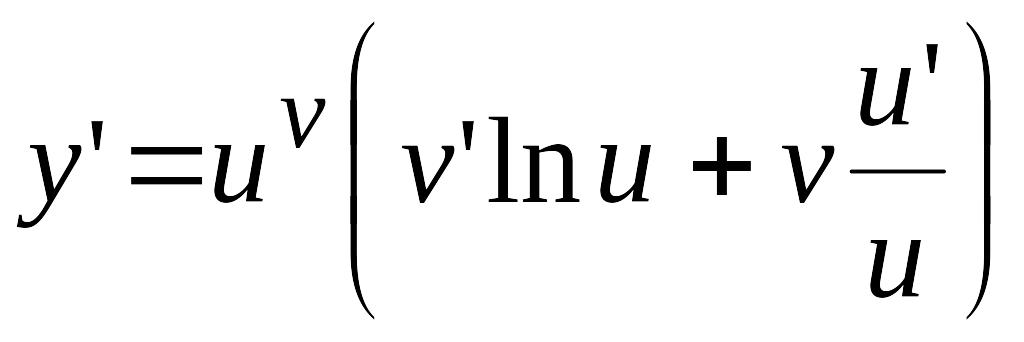 .
.
Зразки розв’язування задач
Приклад
11.(Задача 2.4(а))
Знайдемо
похідну функції
![]() .
.
Розв’язання.
Застосовуючи правило диференціювання складеної функції та формули похідних степеневої та логарифмічної функцій, маємо:
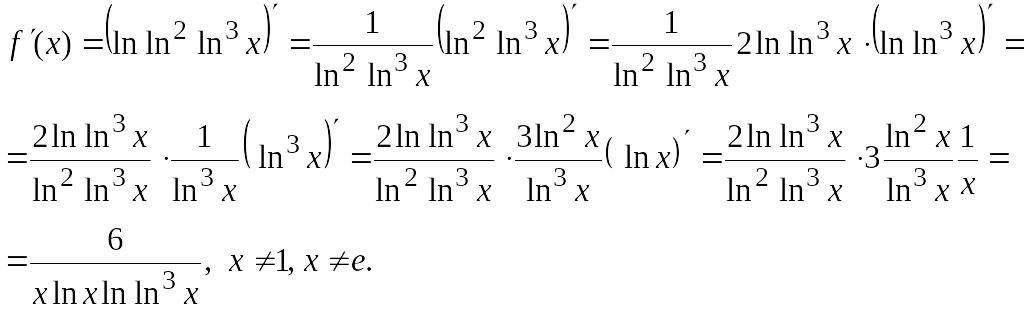
Приклад
12. (Задача
2.4 (б)) Знайдемо
похідну функції
![]() .
.
Розв’язання.
Прологарифмуємо функцію , а потім продиференціюємо, тобто
![]() ,
,
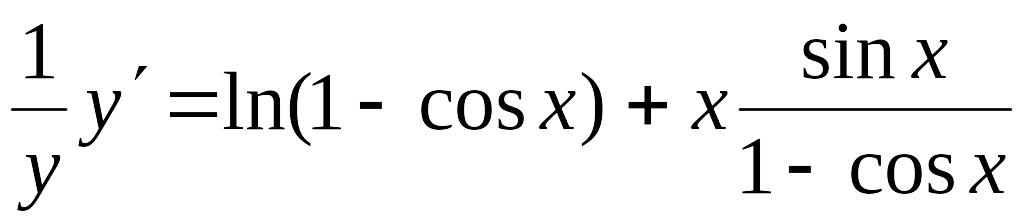 .
.
Таким
чином,
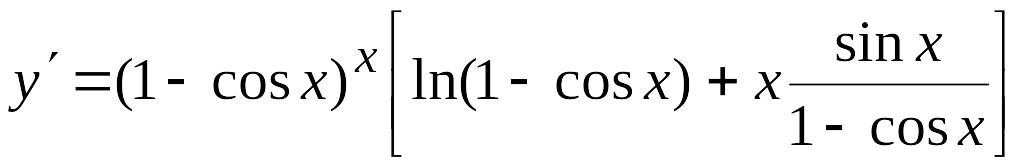 .
.
Приклад 13. (Задача 2.4 (г)) Знайдемо похідну функції, заданої параметрично
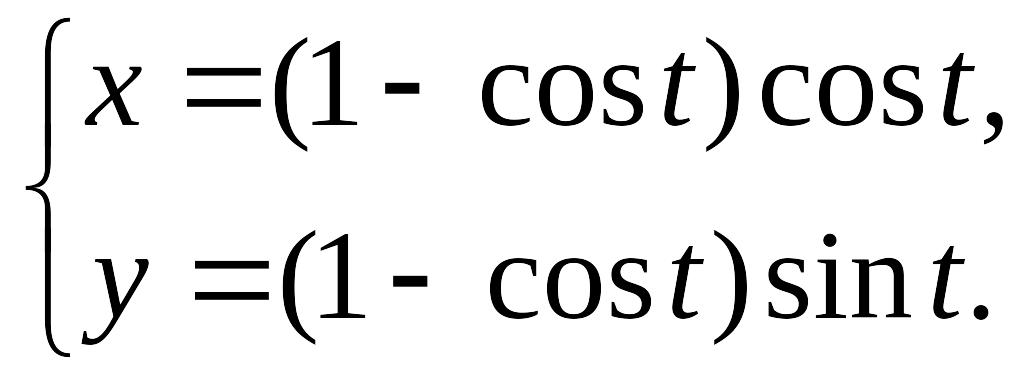
Розв’язання.
Застосовуючи формулу похідної функції, яка задана параметрично, знаходимо:
 .
.
Приклад 14.
Продиференціюємо
функцію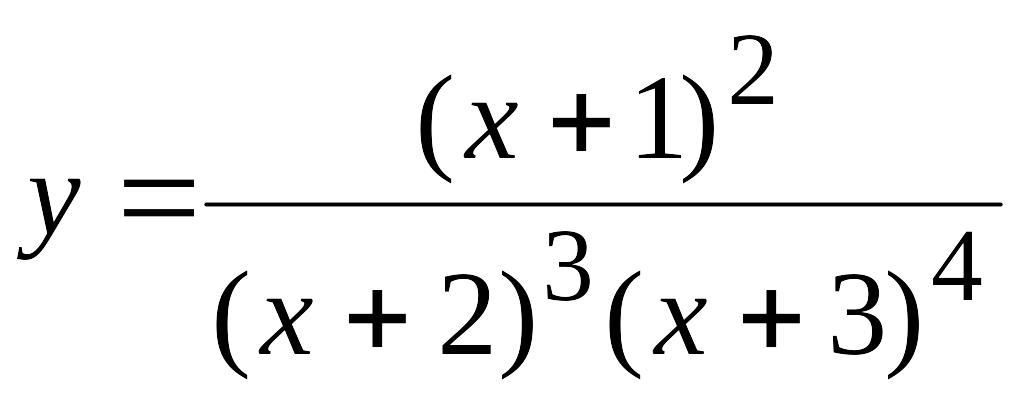 .
.
Розв’язання.
Цю функцію можна диференціювати як частку двох функцій. Але це приведе до складних обчислень. тому краще спочатку прологарифмувати функцію, а потім продиференціювати.
Дійсно,
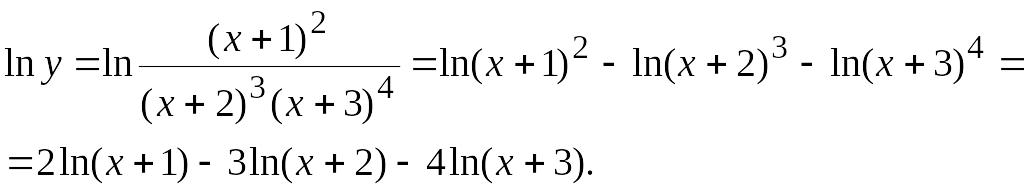
Диференціюючи ( розглядаємо як складену функцію), маємо:
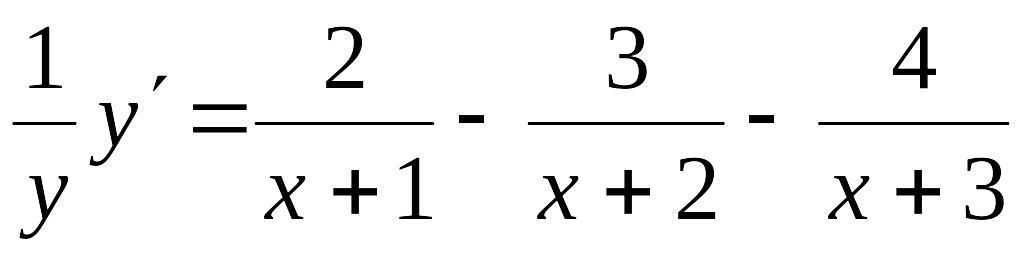 .
.
Тоді
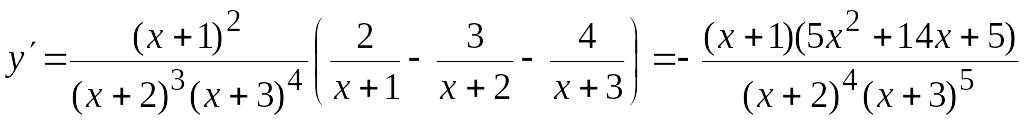 .
.
Диференціал.
Якщо задано диференційовну функцію , то її приріст
![]() ,
(1)
,
(1)
де
![]() ,
коли
,
коли
![]() .
При
величина
.
При
величина
![]() є
величиною нескінченно малою вищого
порядку, ніж
.
Перший доданок у формулі (1)
є
величиною нескінченно малою вищого
порядку, ніж
.
Перший доданок у формулі (1)
![]() є головною частиною приросту функції
в точці
.
Цей доданок і називається диференціалом
функції.
є головною частиною приросту функції
в точці
.
Цей доданок і називається диференціалом
функції.
Диференціалом
функції
називається добуток похідної даної
функції на приріст незалежної змінної.
Диференціал функції позначається
символом
![]() .
.
Диференціалом
незалежної змінної
називається її приріст:
![]() .
.
Тому
![]() .
.
Геометрично
(рис. 5) диференціал функції
являє собою приріст ординати дотичної
до графіка функції в точці
![]() .
.
Приклад 15.
(Задача 2.5) Обчислимо
наближено за допомогою диференціала
значення функції
![]() в точці
в точці
![]() .
.
Розв’язання.
У
формулі застосування диференціала до
наближених обчислень покладемо
![]() .
Тоді
.
Тоді
![]() ,
але
,
але
![]() ,
,
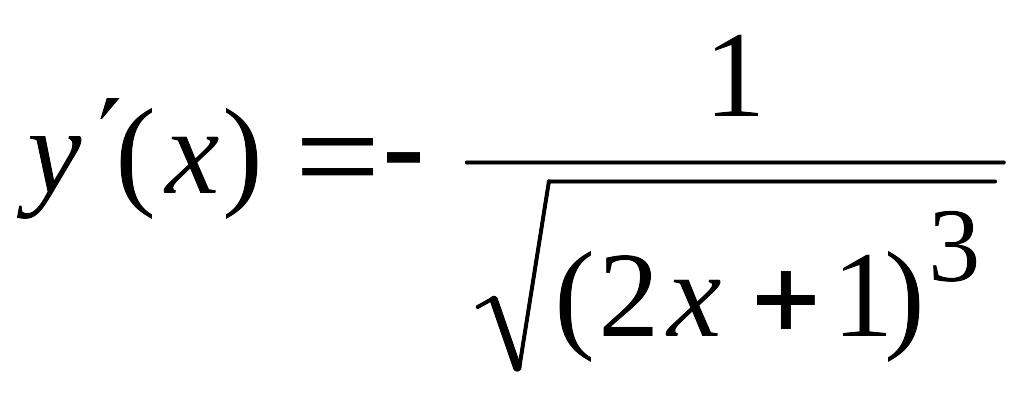 ,
,
![]() .
.
Отже,
![]() .
.
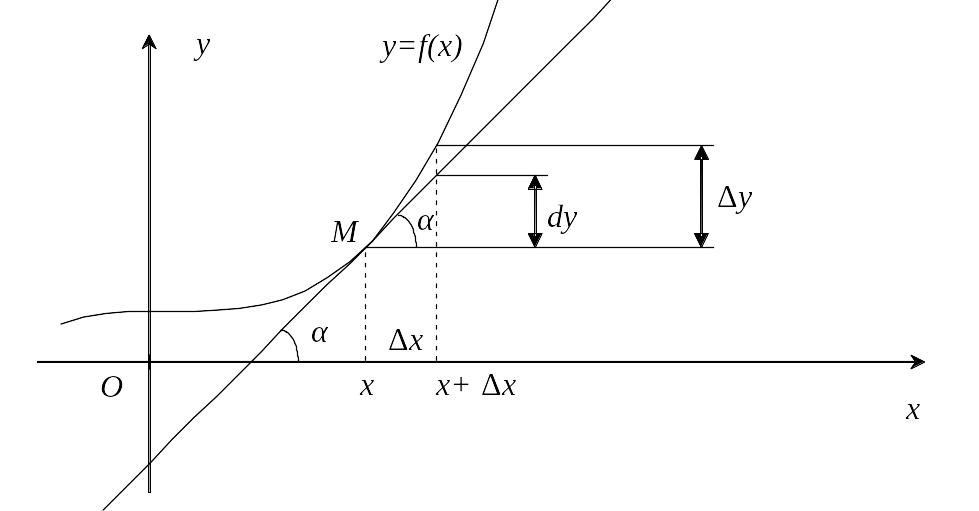
Рис. 5
