
- •Передмова
- •§1. Елементи лінійної алгебри і аналітичної геометрії
- •Елементи лінійної алгебри
- •Системи лінійних алгебраїчних рівнянь
- •Матриця
- •Матричний метод, правило Крамера
- •Зразки розв’язування задач
- •Контрольні запитання
- •1.2 Елементи аналітичної геометрії. Вектори та дії над ними
- •Мішаний добуток векторів.
- •Зразки розв’язування задач
- •Пряма на площині.
- •Контрольні запитання
- •Задачі контрольної роботи №1
- •§ 2. Введення в математичний аналіз. Границя функції
- •Зразки розв’язування задач
- •Контрольні запитання
- •§ 3. Диференціальне числення функції однієї змінної
- •Зразки розв’язування задач
- •Застосування диференціального числення для дослідження функцій
- •Застосування диференціального числення до економічних задач
- •Контрольні запитання
- •Як можна знайти найбільше й найменше значення функції на відрізку? Задачі контрольної роботи №2
- •§4 Диференціальне числення функцій багатьох змінних
- •Зразки розв’язування задач
- •Метод найменших квадратів можливої лінійної залежності між змінними
- •Контрольні запитання
- •§5 Інтегральне числення функції однієї змінної
- •5.1 Невизначений інтеграл
- •Основні методи інтегрування
- •Зразки розв’язування задач
- •5.2 Визначений інтеграл
- •Зразки розв’язування задач
- •5.3 Використання визначеного інтеграла в економіці
- •Зразки розв’язування задач
- •5.4 Невласні інтеграли першого роду
- •Зразки розв’язування задач
- •Контрольні запитання
- •Задачі контрольної роботи №3
- •§6 Диференціальні рівНянНя
- •6.1 Диференціальні рівняння і порядку Диференціальні рівняння з відокремлюваними змінними.
- •Зразки розв’язування задач
- •Однорідні диференціальні рівняння
- •Лінійні диференціальні рівняння
- •6.2 Диференціальні рівняння іі порядку Лінійні диференціальні рівняння іі порядку з сталими коефіцієнтами
- •Зразки розв’язування задач
- •Знаходження частинного розв’язку неоднорідного рівняння методом невизначених коефіцієнтів.
- •Контрольні запитання
- •§7 Ряди
- •Зразки розв’язування задач
- •Знакозмінні ряди
- •Степеневі ряди
- •Контрольні запитання
- •Задачі контрольної роботи №4
- •Література
Знакозмінні ряди
Знакозмінним називається числовий ряд, члени якого можуть бути як додатніми, так і від’ємними.
Розглянемо ряд, знаки членів якого чергуються, тобто ряд довільні два сусідні члени якого мають різні знаки:
![]() , (7.2)
, (7.2)
де
![]() ,
,
![]() .
.
Цей ряд досліджується на збіжність за допомогою такої достатньої ознаки.
Теорема
(Ознака
Лейбніца). Ряд
![]() збіжний, якщо:
збіжний, якщо:
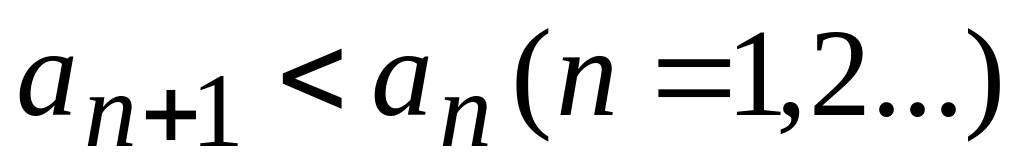 ;
;.
При цьому сума ряду додатня і не перевищує першого його члена.
Ряди, для яких виконується ознака Лейбніца, називаються рядами лейбніцевого типу.
Абсолютна
похибка від заміни суми збіжного ряду
його частинною сумою не перевищує модуля
першого з відкинутих членів ряду, тобто
![]() .
.
Приклад
10.
Довести, що ряд
![]() збіжний і знайти його суму з точністю
до
збіжний і знайти його суму з точністю
до
![]() .
.
Розв’язання.
Перевіримо виконання умов Лейбніца:
знаки членів ряду строго чергуються;
модулі членів ряду спадають
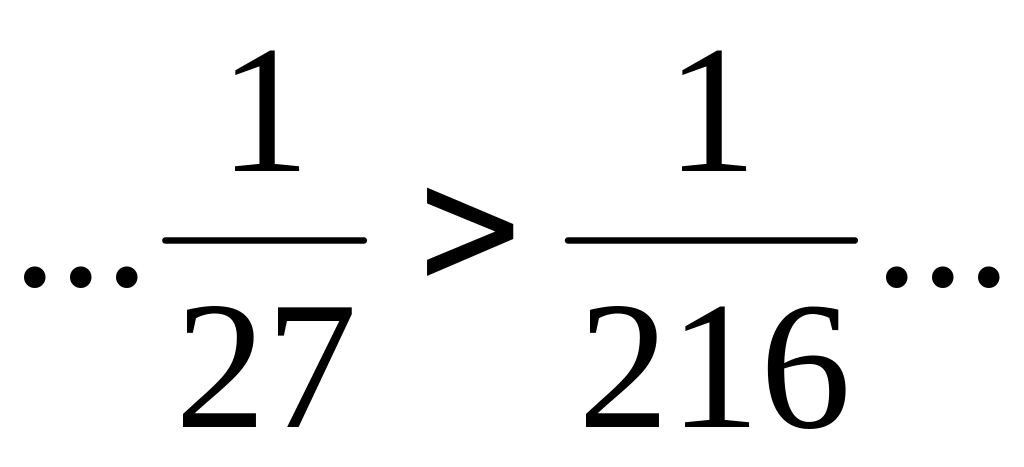 ;
;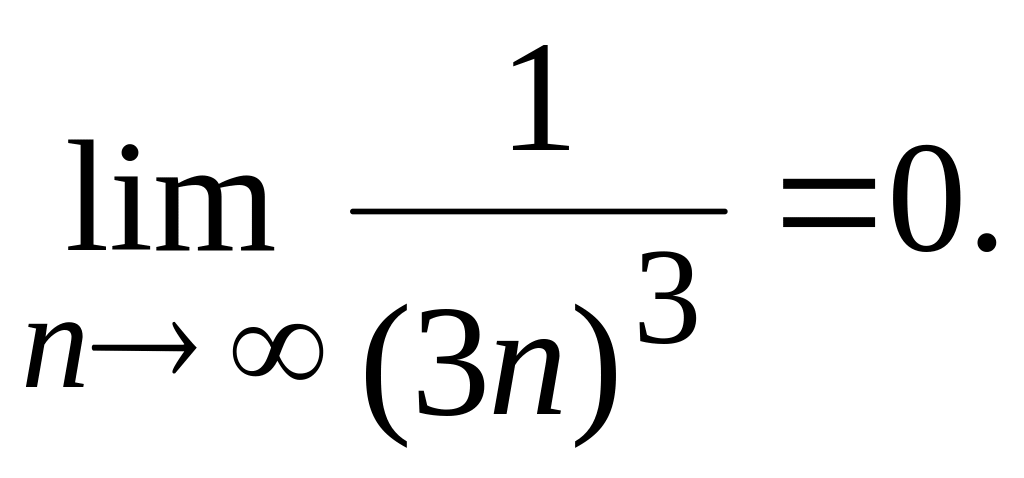
Отже, ряд збіжний і має певну суму .
Для того щоб обчислити суму ряда з точністю до треба взяти стільки його членів, щоб перший з наступних членів був за модулем менший від . Тоді весь залишок ряду, починаючи з цього члена ряда буде менший від . В даному разі маємо:
![]()
тобто,
щоб знайти суму даного ряду з точністю
до
,
досить залишити перші три члени ряду,
а решту відкинути. Таким чином,
![]()
Знакозмінний ряд називається умовно збіжним, якщо ряд (7.2) збіжний, а ряд утворений з модулів його членів розбіжний.
Наприклад.
Ряд
![]() – збіжний і так як ряд
– збіжний і так як ряд
![]() ,
який складається з модулів членів даного
ряду, збіжний, то даний знакозмінний
ряд абсолютно
збіжний.
,
який складається з модулів членів даного
ряду, збіжний, то даний знакозмінний
ряд абсолютно
збіжний.
Ряд
![]() – умовно
збіжний,
так як ряд
– розбіжний, як гармонічний, а ряд
– збіжний за ознакою Лейбніца.
– умовно
збіжний,
так як ряд
– розбіжний, як гармонічний, а ряд
– збіжний за ознакою Лейбніца.
Степеневі ряди
Ряд виду
![]() (7.3)
(7.3)
називається степеневим рядом.
Число
![]() називається радіусом
збіжності
степеневого ряду
називається радіусом
збіжності
степеневого ряду
![]() ,
якщо він абсолютно збіжний при
,
якщо він абсолютно збіжний при
![]() ,
і розбіжний при
,
і розбіжний при
![]() .
При
.
При
![]() ряд може як збігатися, так і розбігатися.
ряд може як збігатися, так і розбігатися.
Інтеграл
![]() називається областю
збіжності
степеневого ряду. Радіус збіжності
може бути знайдений по формулі:
називається областю
збіжності
степеневого ряду. Радіус збіжності
може бути знайдений по формулі:
![]() (7.4)
(7.4)
Приклад
11. (Задача 4.4)
Знайти область збіжності степеневого
ряду
![]() .
.
Розв’язання.
Радіус
збіжності знаходимо за формулою (7.4) :
![]() ,
,
![]() .
.
![]() .
.
Інтервал
збіжності даного ряду визначається
нерівністю
![]() або
або
![]() .
.
Дослідимо кінці інтервала збіжності:
при
 ,
одержуємо числовий ряд:
,
одержуємо числовий ряд:
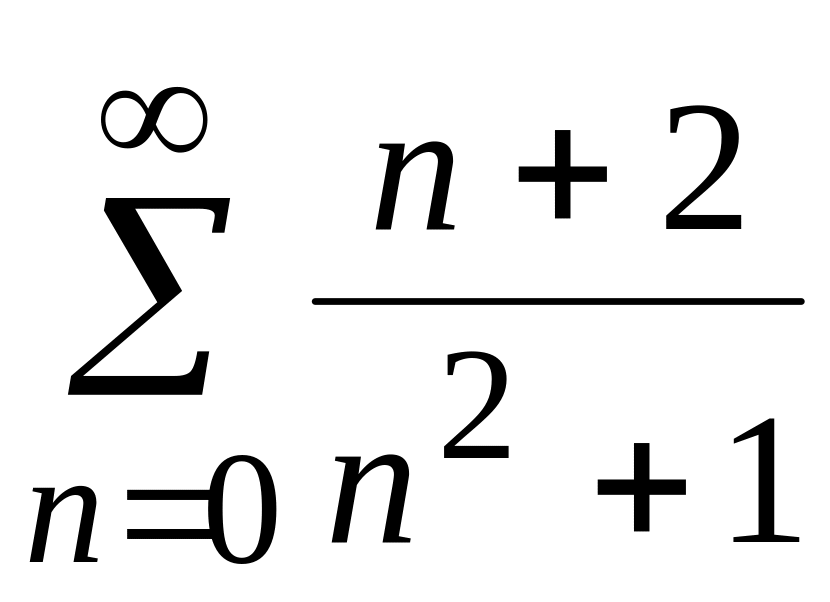 .
Застосуємо граничну ознаку порівняння.
Для порівняння візьмемо гармонічний
ряд
– який розбіжний,
.
Застосуємо граничну ознаку порівняння.
Для порівняння візьмемо гармонічний
ряд
– який розбіжний,
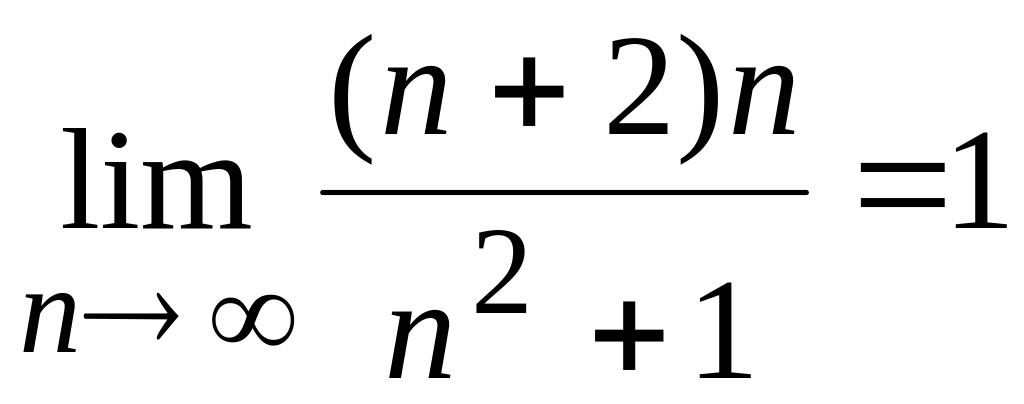 ,
отже ряди
,
ведуть себе однаково. Тому ряд
теж розбіжний.
,
отже ряди
,
ведуть себе однаково. Тому ряд
теж розбіжний.при
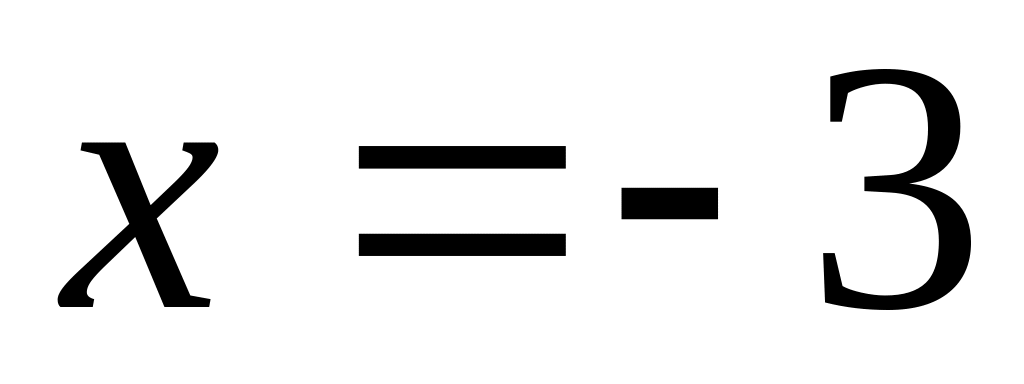 одержуємо знакозмінний ряд
одержуємо знакозмінний ряд
 .
Ряд збіжний за ознакою Лейбніца. Так
як ряд складений з модулів членів даного
ряду
розбіжний, то даний ряд умовно збіжний.
.
Ряд збіжний за ознакою Лейбніца. Так
як ряд складений з модулів членів даного
ряду
розбіжний, то даний ряд умовно збіжний.
Таким
чином, інтервал збіжності досліджуваного
степеневого ряду має вигляд
![]() .
.
Контрольні запитання
Що таке числовий ряд? Які має властивості?
Як формулюється необхідна ознака збіжності числового ряду?
Як формулюється ознаки порівняння, ознака Д’Аламбера, радикальна ознака Коші?
Які ряди називаються знакозмінними?
Сформулювати теорему Лейбніца.
Які ряди називаються степеневими?
Що таке інтервал збіжності степеневого ряду, чим він відрізняється від області збіжності?
