6.2 Диференціальні рівняння іі порядку Лінійні диференціальні рівняння іі порядку з сталими коефіцієнтами
Рівняння
виду
дійсні
числа, причому
називається лінійним
диференціальним рівнянням
порядку зі сталими коефіцієнтами.
Якщо
,
то рівняння
,
називається однорідним, а якщо
– неоднорідним.
Квадратне
рівняння називається характеристичним
рівнянням диференціального
рівняння
.
Нехай
– дискримінант квадратного рівняння.
Можливі наступні випадки:
– тоді
загальним розв’язком рівняння
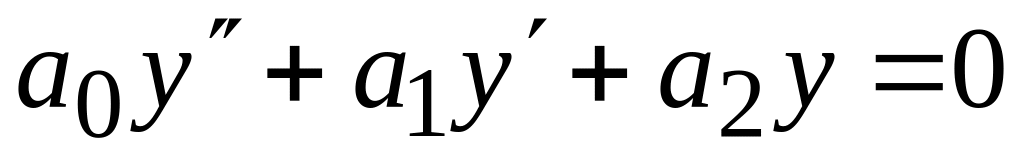являється функція
(
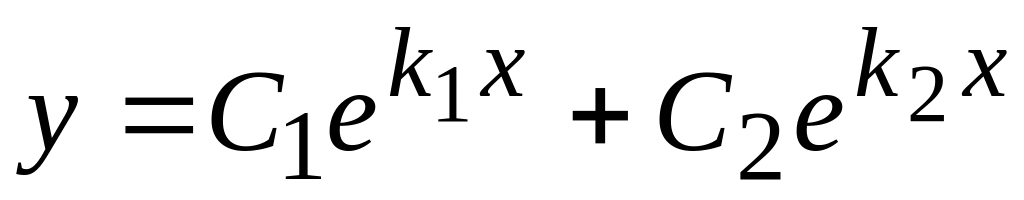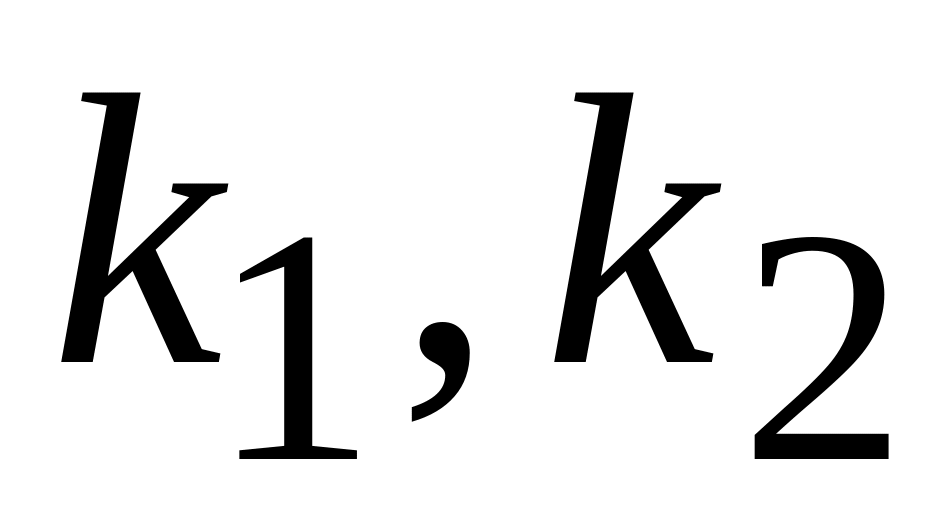– корені характеристичного рівняння);
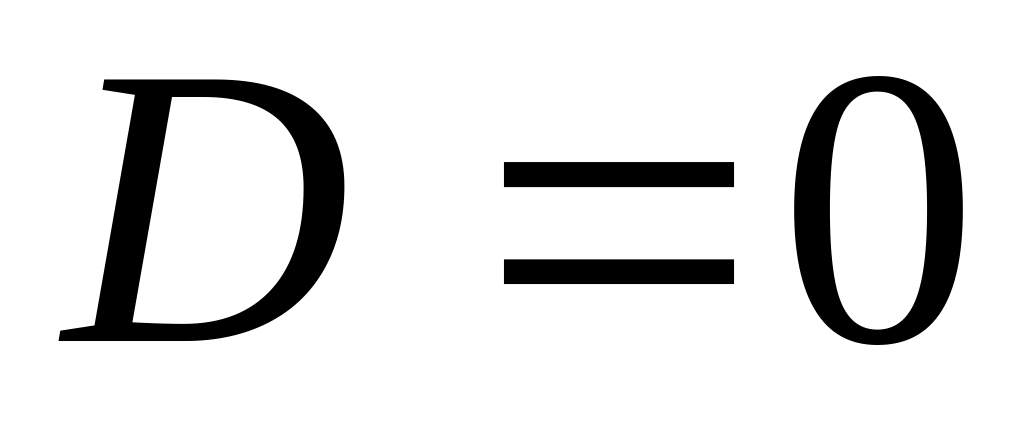– загальним
розв’язком являється функція
(
–
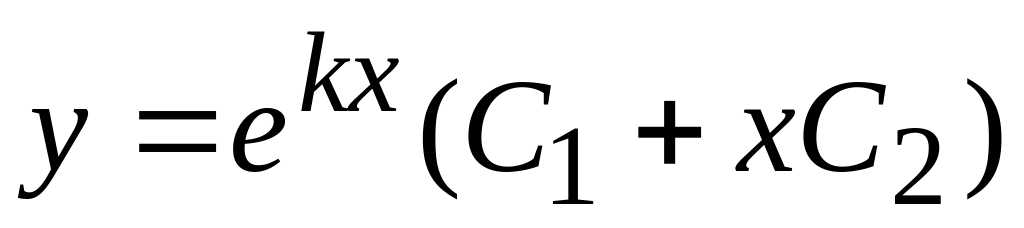корінь характеристичного рівняння);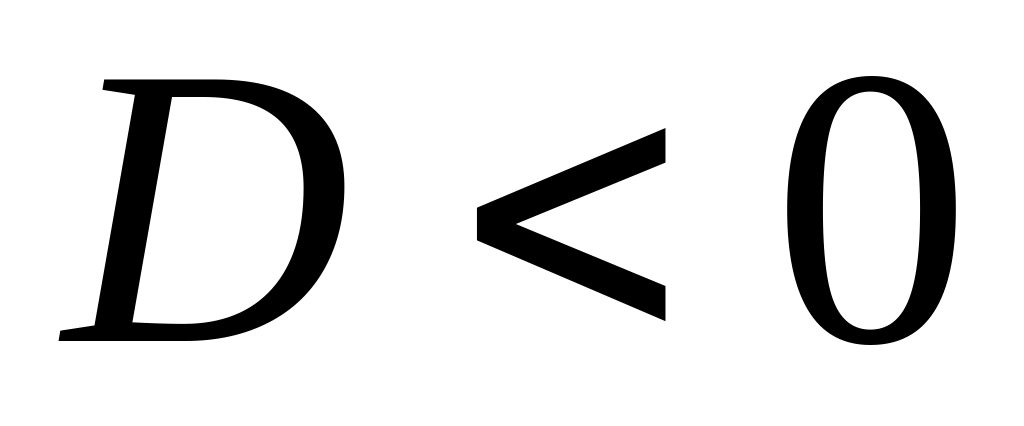
,
тоді якщо
– корені характеристичного рівняння,
то загальним розв’язком рівняння
являється функція
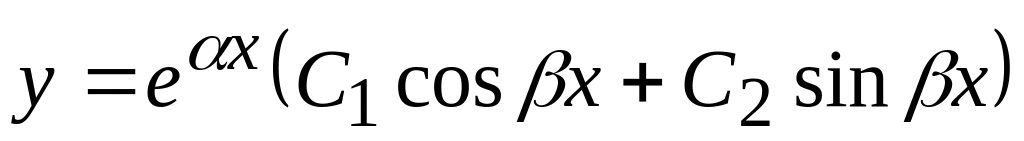
Зразки розв’язування задач
Приклад 4. Знайти загальний розв’язок диференціальних рівнянь:
а)
.
Розв’язання.
Складаємо
і розв’язуємо характеристичне рівняння:
корені дійсні і різні, отже загальний
розв’язок даного рівняння:
.
б)
.
Розв’язання.
Характеристичне
рівняння
має рівні корені
,
тому загальний розв’язок запишемо у
вигляді
.
в)
.
Розв’язання.
Характеристичне
рівняння:
,
тому
,
отже
.
Корені комплексні. Загальний розв’язок:
.
Теорема.
Загальний розв’язок неоднорідного
диференціального рівняння
має вигляд
,
де
– загальний розв’язок відповідного
однорідного рівняння
,
а
– деякий частинний розв’язок неоднорідного
диференціального рівняння.
Знаходження частинного розв’язку неоднорідного рівняння методом невизначених коефіцієнтів.
1.
Нехай права частина рівняння многочлен
степеня, тобто
,
тоді:
а) Якщо
не являється коренем характеристичного
рівняння, тоді частинний розв’язок
матиме вигляд:
,
зокрема:
і т.д.
б) Якщо
є коренем характеристичного рівняння,
тоді частинний розв’язок матиме вигляд:
.
2.
,
тоді:
а) Якщо
– не являється коренем характеристичного
рівняння, частинний розв’язок матиме
вигляд:
.
б) Якщо
– являється
-
кратним коренем характеристичного
рівняння, тоді:
.
3.
.
а) Якщо
– не являється коренем характеристичного
рівняння, тоді:
,
де
.
б) Якщо
– являється коренем характеристичного
рівняння , тоді:
.
4.
а) Якщо
– не являється коренем характеристичного
рівняння, тоді:
,
де
.
б) Якщо
– являється коренем характеристичного
рівняння , тоді:
.
Зауваження.
Ми розглядаємо лише диференціальні
рівняння
порядку.
З диференціальними рівняннями вищих
порядків можна самостійно познайомитись
з вказаної літератури.
Приклад 5. (Задача 4.2). Знайти розв’язок задачі Коші.
Розв’язання.
Знайдемо
спочатку загальний розв’язок рівняння:
,
який має вигляд
.
а)
– це загальний розв’язок відповідного
даному однорідного рівняння:
.
Запишемо його характеристичне рівняння:
отже
.
б)
– частинний розв’язок даного рівняння
будемо шукати методом невизначених
коефіцієнтів у вигляді
(випадок
2(б))
Отже,
Так як
розв’язок рівняння, то підставивши
його в рівняння одержимо рівність:
.
.
Отже,
загальний розв’язок даного рівняння:
.
Використавши
задані початкові умови знайдемо частинний
розв’язок рівняння (задачі Коші). Для
цього знайдемо
Підставимо
початкові умови в
і
одержимо:
,
Таким
чином,
.
2.
.
Загальний розв’язок даного рівняння , отже:
а)
– це загальний розв’язок відповідного
даному однорідного рівняння:
.
Знайдемо корені відповідного йому
характеристичного рівняння
.
Отже,
.
б)
:
Так як права частина
– многочлен
степеня, причому
не є коренем характеристичного рівняння,
то його частинний розв’язок будемо
шукати у вигляді:
(випадок 1(а)):
,
.
Підставимо
в дане рівняння:
Прирівняємо коефіцієнти при однакових степенях:
-
,
,
,
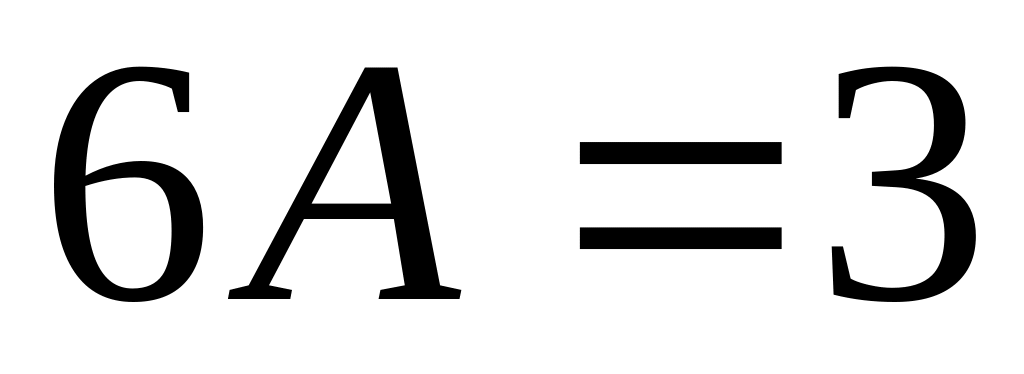
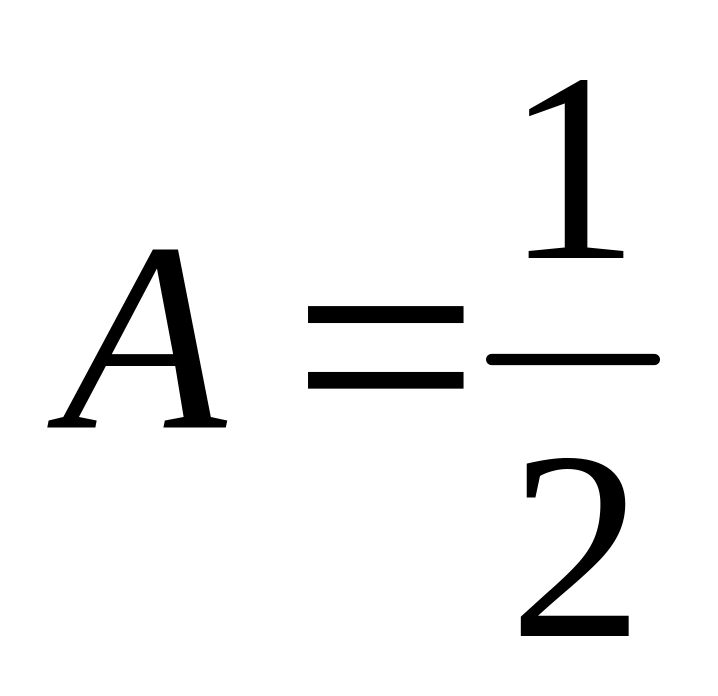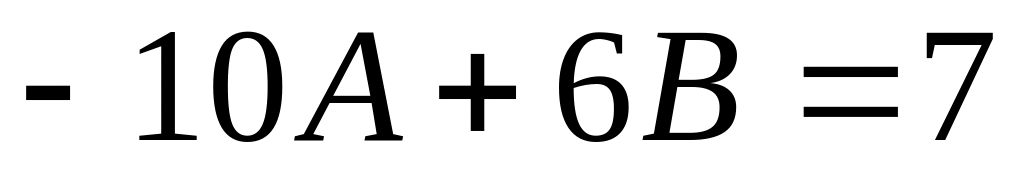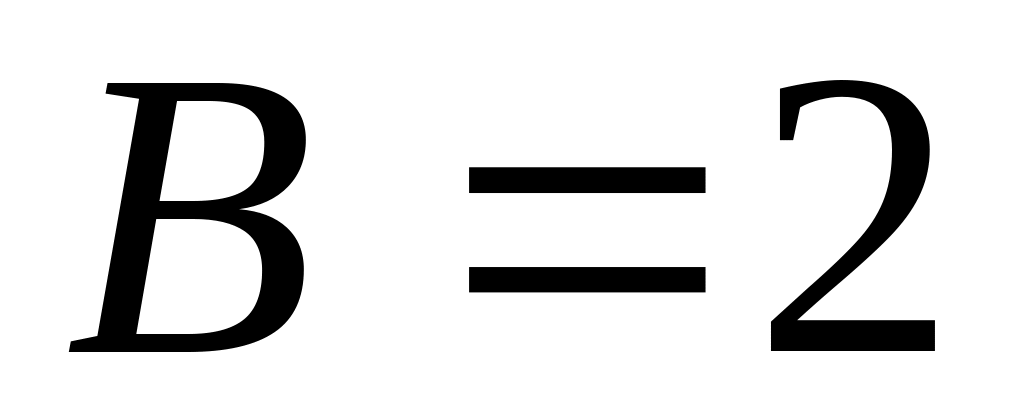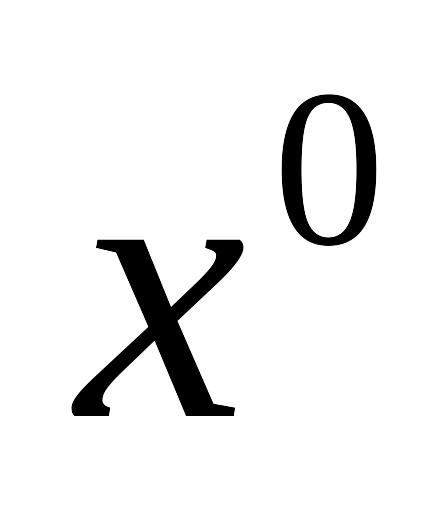
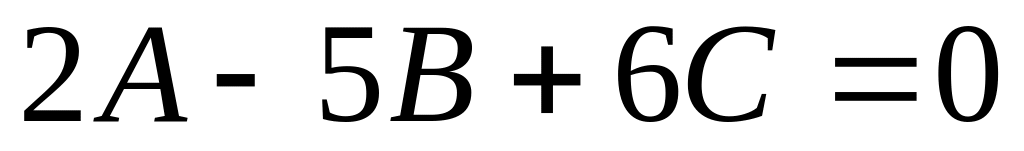
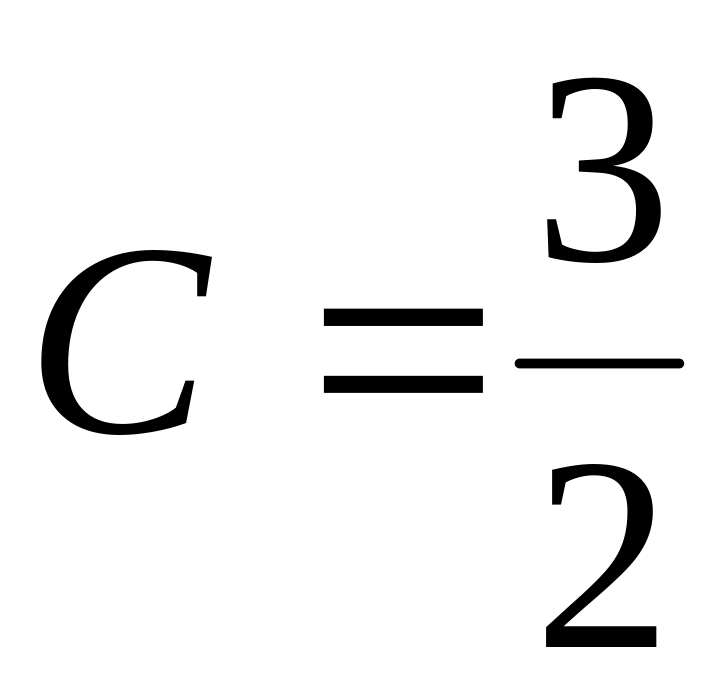
Таким чином
Запишемо загальний розв'язок даного неоднорідного рівняння:
.
Знайдемо розв’язок задачі Коші.
Так як
,
то
.
Знайдемо
.
отже
.
Із
системи рівнянь:
знайдемо
.
Таким чином, запишемо відповідь:
.