
- •Передмова
- •§1. Елементи лінійної алгебри і аналітичної геометрії
- •Елементи лінійної алгебри
- •Системи лінійних алгебраїчних рівнянь
- •Матриця
- •Матричний метод, правило Крамера
- •Зразки розв’язування задач
- •Контрольні запитання
- •1.2 Елементи аналітичної геометрії. Вектори та дії над ними
- •Мішаний добуток векторів.
- •Зразки розв’язування задач
- •Пряма на площині.
- •Контрольні запитання
- •Задачі контрольної роботи №1
- •§ 2. Введення в математичний аналіз. Границя функції
- •Зразки розв’язування задач
- •Контрольні запитання
- •§ 3. Диференціальне числення функції однієї змінної
- •Зразки розв’язування задач
- •Застосування диференціального числення для дослідження функцій
- •Застосування диференціального числення до економічних задач
- •Контрольні запитання
- •Як можна знайти найбільше й найменше значення функції на відрізку? Задачі контрольної роботи №2
- •§4 Диференціальне числення функцій багатьох змінних
- •Зразки розв’язування задач
- •Метод найменших квадратів можливої лінійної залежності між змінними
- •Контрольні запитання
- •§5 Інтегральне числення функції однієї змінної
- •5.1 Невизначений інтеграл
- •Основні методи інтегрування
- •Зразки розв’язування задач
- •5.2 Визначений інтеграл
- •Зразки розв’язування задач
- •5.3 Використання визначеного інтеграла в економіці
- •Зразки розв’язування задач
- •5.4 Невласні інтеграли першого роду
- •Зразки розв’язування задач
- •Контрольні запитання
- •Задачі контрольної роботи №3
- •§6 Диференціальні рівНянНя
- •6.1 Диференціальні рівняння і порядку Диференціальні рівняння з відокремлюваними змінними.
- •Зразки розв’язування задач
- •Однорідні диференціальні рівняння
- •Лінійні диференціальні рівняння
- •6.2 Диференціальні рівняння іі порядку Лінійні диференціальні рівняння іі порядку з сталими коефіцієнтами
- •Зразки розв’язування задач
- •Знаходження частинного розв’язку неоднорідного рівняння методом невизначених коефіцієнтів.
- •Контрольні запитання
- •§7 Ряди
- •Зразки розв’язування задач
- •Знакозмінні ряди
- •Степеневі ряди
- •Контрольні запитання
- •Задачі контрольної роботи №4
- •Література
Застосування диференціального числення для дослідження функцій
Монотонність
функції.
Якщо
диференційовна на інтервалі
![]() і
і
![]() всюди, крім, можливо, скінченого числа
точок, в яких
всюди, крім, можливо, скінченого числа
точок, в яких
![]() на
,
то функція
зростає
(спадає)
на
.
на
,
то функція
зростає
(спадає)
на
.
Інтервали монотонності функції (інтервали спадання чи зростання) відділяються один від одного точками, де похідна функції рівна нулю або не існує. Дані точки називаються критичними точками.
Щоб
знайти інтервали монотонності функції
,
необхідно: 1) знайти область визначення
функції; 2) знайти похідну даної функції;
3) знайти критичні точки з рівняння
та з умови, що
![]() не існує; 4) розділити критичними точками
область визначення на інтервали і в
кожному з них визначити знак похідної.
На інтервалах, де похідна додатна,
функція зростає, а де від’ємна – спадає.
не існує; 4) розділити критичними точками
область визначення на інтервали і в
кожному з них визначити знак похідної.
На інтервалах, де похідна додатна,
функція зростає, а де від’ємна – спадає.
Локальний екстремум. Достатні умови екстремуму:
Правило 1.
Якщо
– критична точка функції
і при довільному малому
![]() виконуються нерівності
виконуються нерівності
![]() ,
то функція
в
точці
має максимум; якщо ж
,
то функція
в
точці
має максимум; якщо ж
![]() ,то
в точці
має мінімум; якщо ж знаки
,то
в точці
має мінімум; якщо ж знаки
![]() і
і
![]() однакові, то функція
в точці
екстремуму не має.
однакові, то функція
в точці
екстремуму не має.
Правило 2.
Якщо
![]() то функція
в точці має екстремум, а саме максимум,
якщо
то функція
в точці має екстремум, а саме максимум,
якщо
![]() ,
і мінімум, якщо
,
і мінімум, якщо
![]() .
.
Для
знаходження найбільшого (найменшого)
значення функції
на відрізку
![]() необхідно із значень функції на кінцях
відрізка і в критичних точках, які
належать даному відрізку, вибрати
найбільше (найменше).
необхідно із значень функції на кінцях
відрізка і в критичних точках, які
належать даному відрізку, вибрати
найбільше (найменше).
Приклад
16.
(Задача
2.6)
Знайдемо
найбільше та найменше значення функції
 на відрізку
на відрізку
![]() .
.
Розв’язання.
Знаходимо екстремуми функції. Для цього обчислюємо першу похідну функції
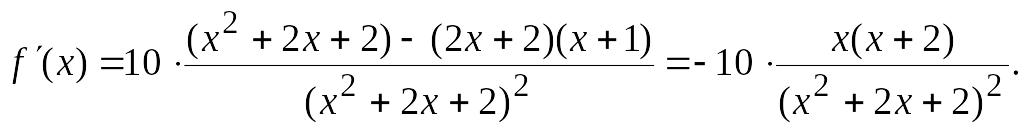
Функція
має дві критичні точки
![]() .
Але точка
.
Але точка
![]() не належить відрізку
.
В точці
не належить відрізку
.
В точці
![]() функція має максимум, причому
функція має максимум, причому
![]() .
Обчислимо значення функції
на кінцях відрізка:
.
Обчислимо значення функції
на кінцях відрізка:
![]() .
.
Таким
чином, найбільше значення дана функція
на відрізку
набуває в точці
![]() ,
а найменше – в точці
,
а найменше – в точці
![]() .
.
Опуклість. Увігнутість. Точки перегину. Графік функції називається опуклим (увігнутим) на інтервалі , якщо він розташований нижче (вище) дотичної, проведеної в довільній точці графіка над даним інтервалом.
Достатні умови опуклості (увігнутості) графіка функції: Якщо на інтервалі , то графік функції опуклий на вказаному інтервалі; якщо , то графік функції увігнутий на інтервалі .
Точка
![]() графіка функції, яка відділяє його
опуклу частину від увігнутої називається
точкою
перегину.
В абсцисах точок перегину друга похідна
функції дорівнює нулю або не існує (
графіка функції, яка відділяє його
опуклу частину від увігнутої називається
точкою
перегину.
В абсцисах точок перегину друга похідна
функції дорівнює нулю або не існує (![]() або
або
![]() – не
існує).
Точки, в яких
або не існує, називають критичними
точками другого роду.
– не
існує).
Точки, в яких
або не існує, називають критичними
точками другого роду.
Якщо
– критична
точка другого роду і при довільному
достатньо малому
виконуються нерівності
![]() або
або
![]() ,
то точка кривої
з абсцисою
є точкою перегину.
,
то точка кривої
з абсцисою
є точкою перегину.
Асимптоти.
Пряма
![]() називається асимптотою кривої
,
якщо відстань від точки
кривої до прямої
прямує до нуля при необмеженому віддаленні
даної точки по кривій від початку
координат.
називається асимптотою кривої
,
якщо відстань від точки
кривої до прямої
прямує до нуля при необмеженому віддаленні
даної точки по кривій від початку
координат.
Пряма
![]() є вертикальною асимптотою кривої
,
якщо
є вертикальною асимптотою кривої
,
якщо
![]() .
.
Пряма
![]() є горизонтальною асимптотою кривої
,
якщо існує границя
є горизонтальною асимптотою кривої
,
якщо існує границя
![]() або
або
![]() .
.
Пряма
![]() є похилою асимптотою кривої
,
якщо існують границі:
є похилою асимптотою кривої
,
якщо існують границі:
![]()
або
![]()
Схема дослідження функції та побудова графіка.
Знайти область визначення функції, інтервали неперервності, точки розриву.
Знайти (якщо це можливо) точки перетину графіка з координатними осями.
Дослідити функцію на періодичність, парність і непарність.
Знайти інтервали монотонності, точки локальних екстремумів та значення функції у цих точках.
Знайти інтервали опуклості, ввігнутості та перегину.
Дослідження функції на межі області існування. Асимптоти графіка.
Побудувати графік функції, враховуючи дослідження.
Приклад 17. (Задача 2.7) Дослідити методами диференціаль-ного числення функцію
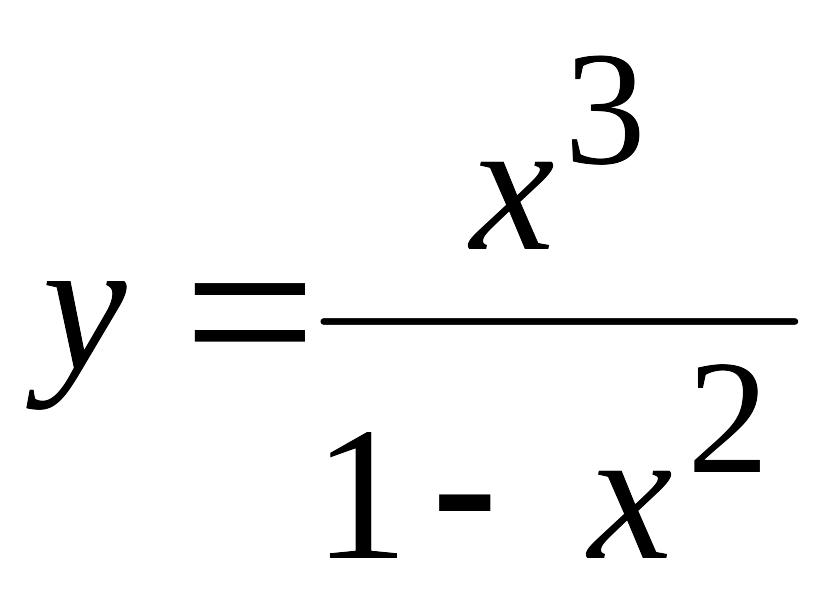
та побудувати її графік.
Розв’язання.
Область визначення:
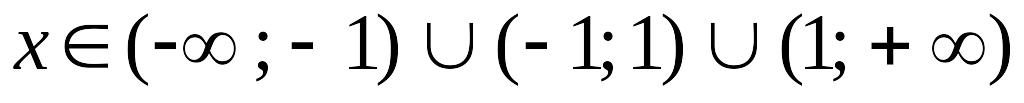 .
Точки розриву
.
Точки розриву
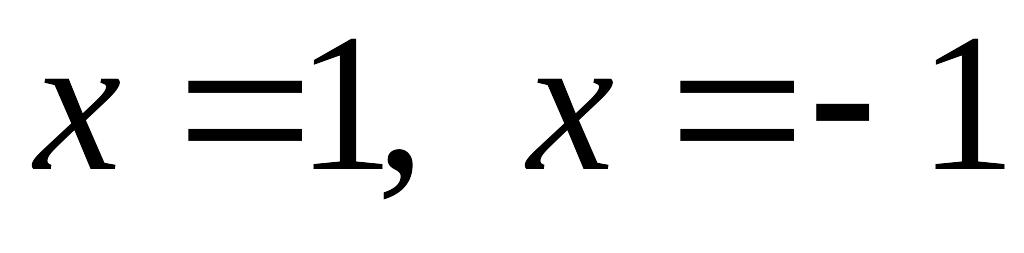 .
.Якщо , то
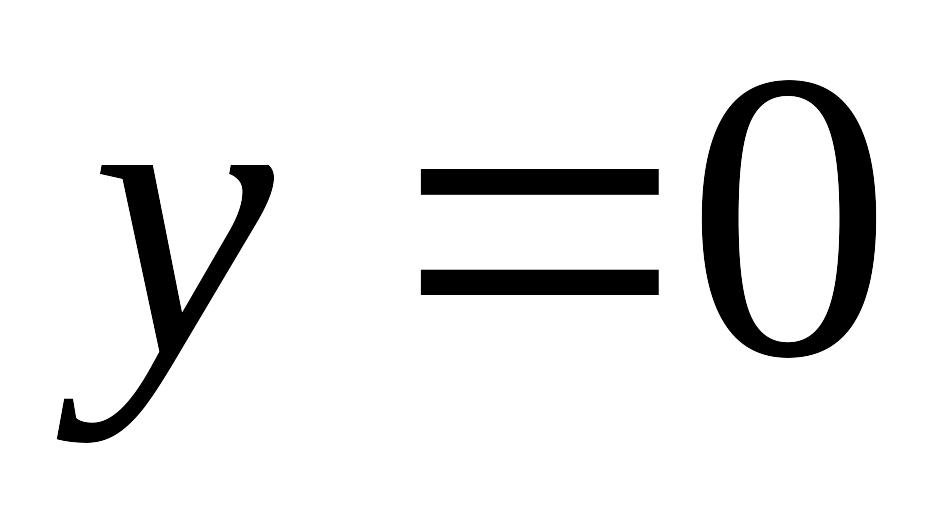 ,
тому графік перетинає осі координат в
точці
,
тому графік перетинає осі координат в
точці
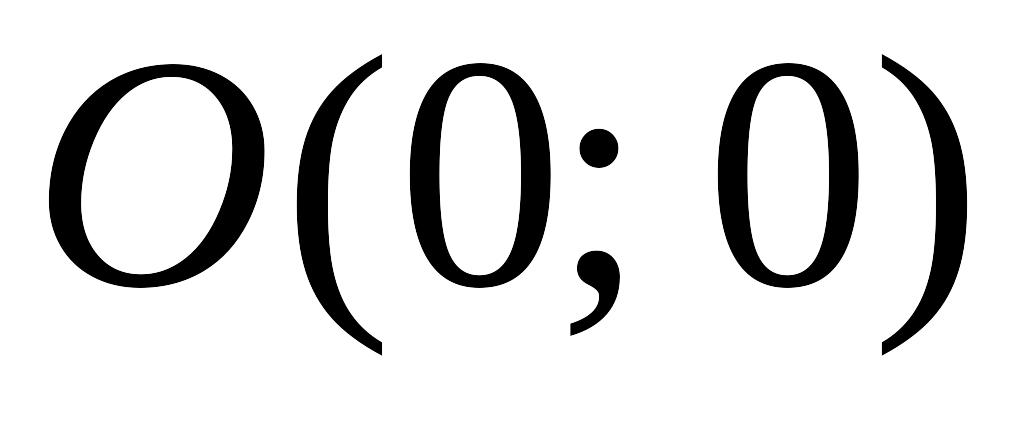 .
.Функція не періодична. Оскільки
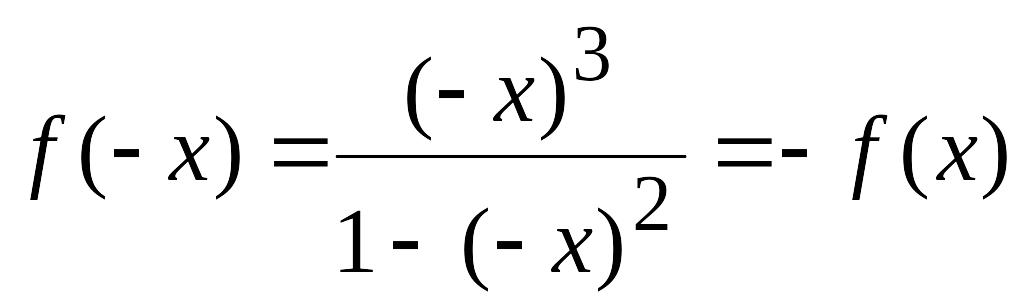 ,
то функція непарна, а отже графік функції
симетричний відносно початку координат.
,
то функція непарна, а отже графік функції
симетричний відносно початку координат.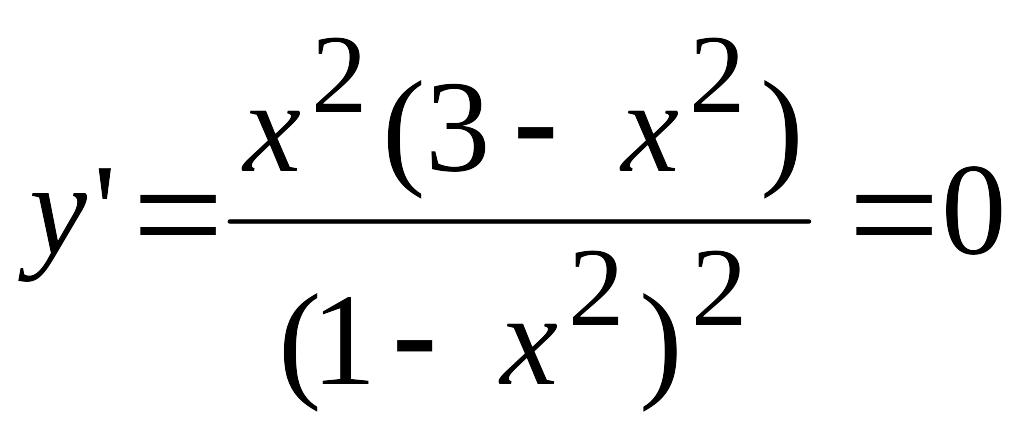 .
Розв’язком даного рівняння є
.
Розв’язком даного рівняння є
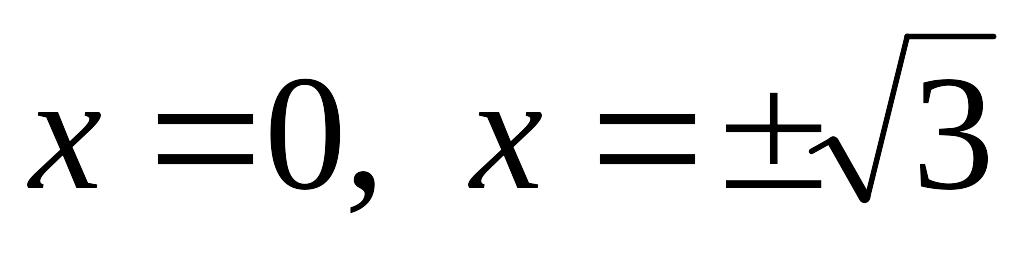 .
Похідна не існує в
.
Похідна не існує в
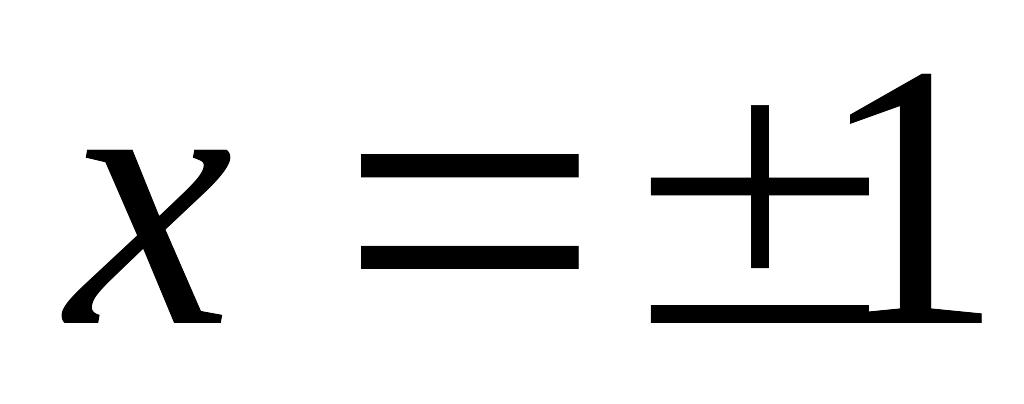 .
Знайдемо знаки
на проміжках:
.
Знайдемо знаки
на проміжках:
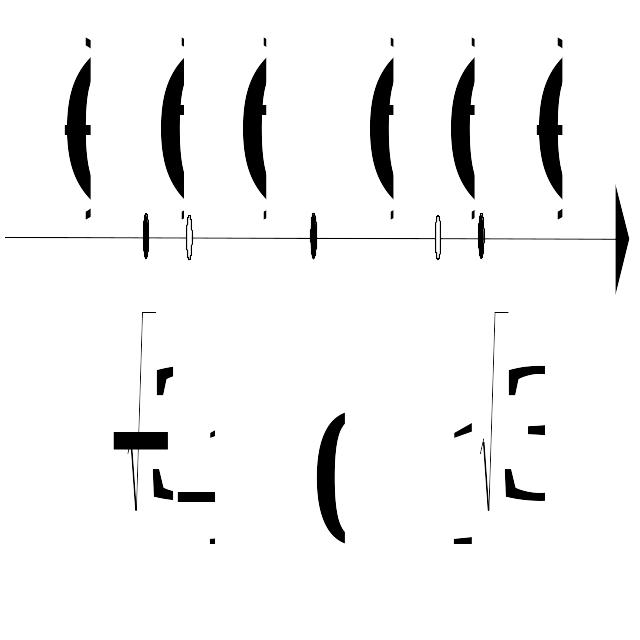
Отже,
на
![]() – функція спадає,
на
– функція спадає,
на
![]() – функція
зростає,
на
– функція
зростає,
на
![]() – функція спадає.
– функція спадає.
У точках
![]() функція
має локальний екстремум:
функція
має локальний екстремум:
![]() – локальний
максимум,
– локальний
максимум,
![]() – локальний мінімум.
– локальний мінімум.
Знаходимо
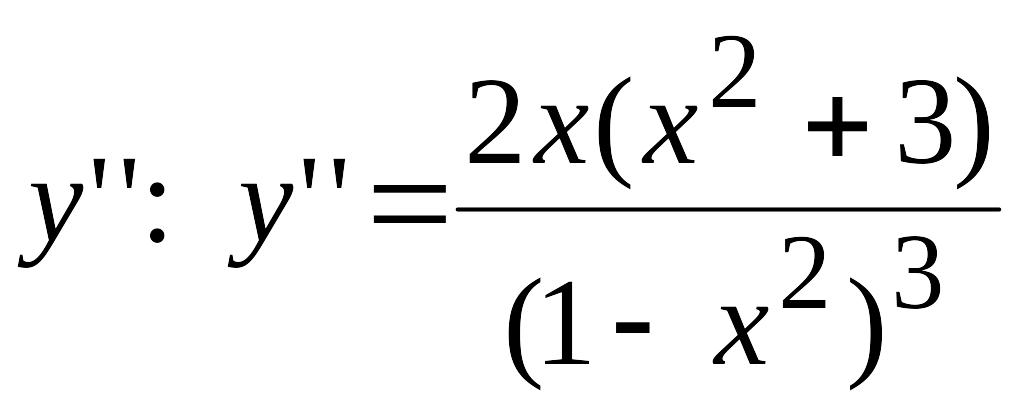 .
Похідна
.
Похідна
 при
і не існує при
.
Знайдемо
знаки
при
і не існує при
.
Знайдемо
знаки
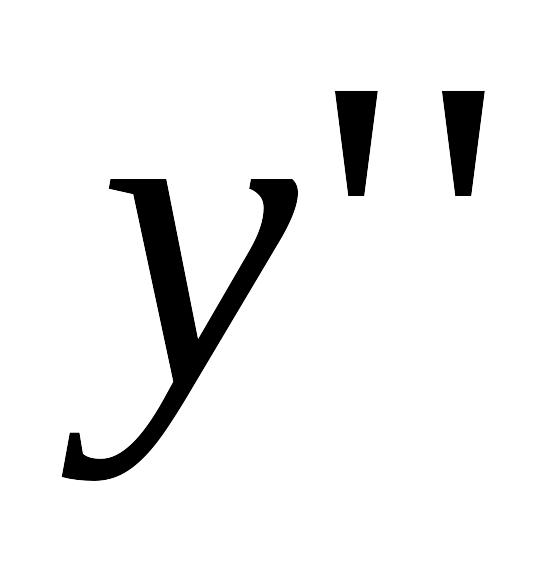 на проміжках:
на проміжках:

Отже,
на
![]() –
крива ввігнута, на
–
крива ввігнута, на
![]() – крива опукла.
– крива опукла.
– вертикальні асимптоти кривої. Знайдемо похилу асимптоту кривої .
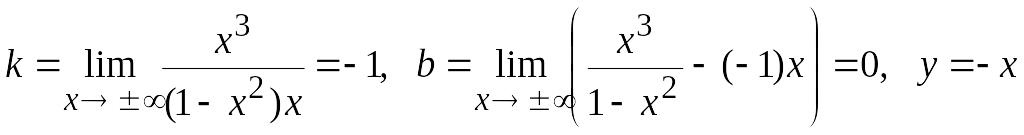 – похила
асимптота.
– похила
асимптота.
Враховуючи проведені дослідження будуємо графік функції.
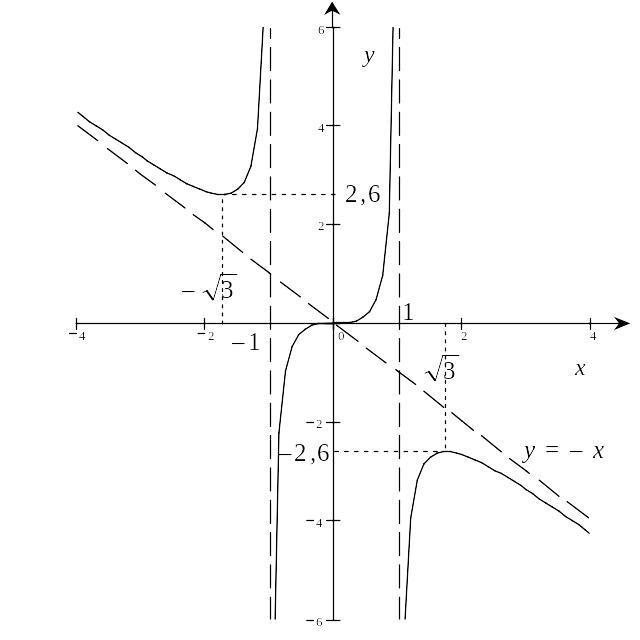
Рис. 6
