Системи лінійних алгебраїчних рівнянь

Нехай задано систему лінійних рівнянь з невідомими

(1.4)

де – коефіцієнти системи, – вільні члени.

Матриця

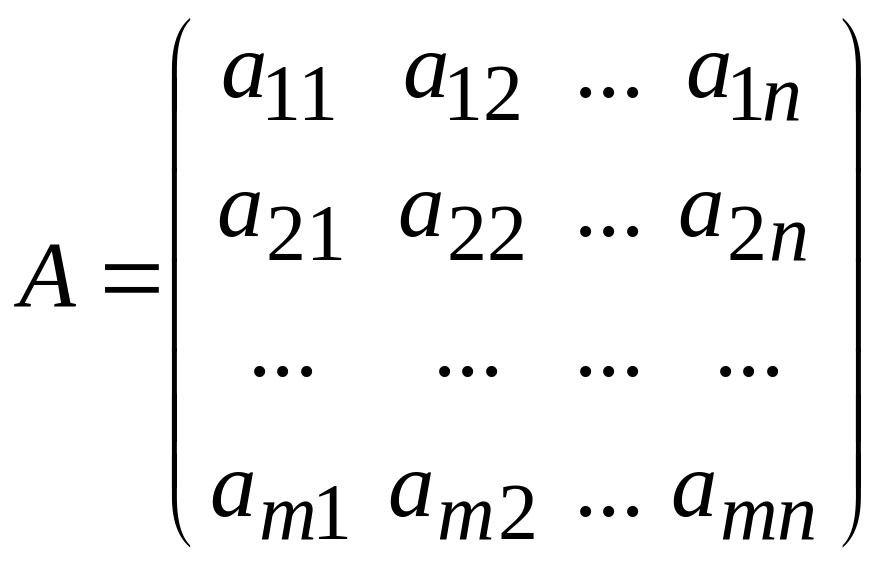
називається матрицею системи.

Матриця

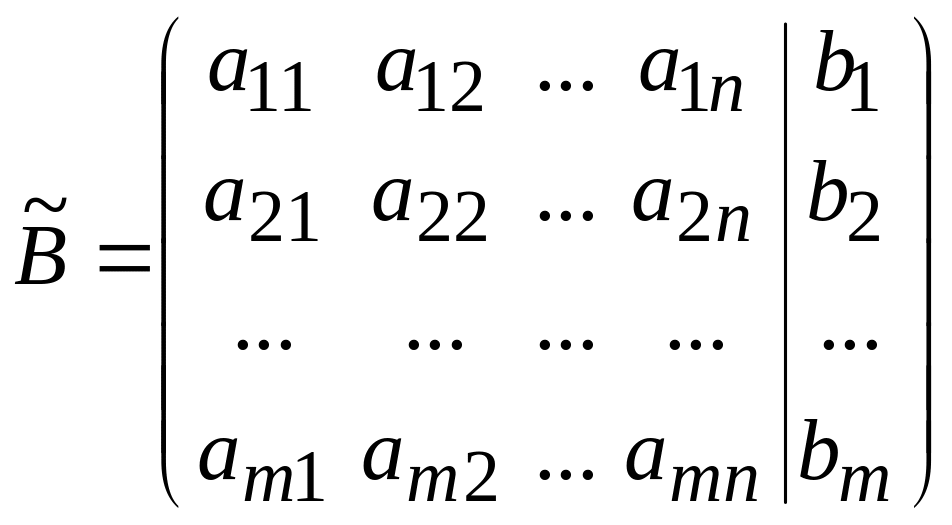
називається розширеною матрицею системи.

Розв'язком системи (1.4) називається впорядкований набір чисел , підстановка яких замість невідомих перетворює всі рівняння системи на арифметичні тотожності.

Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок. Якщо ж система не має жодного розв’язку, то вона називається несумісною.

Позначимо через Х та В матриці-стовпці

,

складені з невідомих і вільних членів системи (1.4), тоді її матрична форма має вигляд

, (1.5)

Матричний метод, правило Крамера

Нехай в системі (1.4) кількість невідомих дорівнює кількості рівнянь , тоді основна матриця системи квадратна.

Якщо ( – визначник системи), то існує обернена до матриця і єдиний розв’язок системи можна знайти матричним методом за формулою

, (1.6)

або за формулами Крамера

(1.7)

де – визначники, що отримуються з визначника заміною -го стовпця стовпцем вільних членів.

Розглянемо систему (1.4) лінійних рівнянь з невідомими у загальному випадку. Питання про сумісність такої системи розв'язує наступна теорема.

Теорема Кронекера-Капеллі.

Система лінійних рівнянь сумісна тоді і тільки тоді, коли ранг основної матриці дорівнює рангу розширеної матриці цієї системи, тобто

.

За цією теоремою, якщо ранги основної та розширеної матриць не рівні, то система несумісна й немає сенсу її розв'язувати. Якщо ранги матриць рівні, то система сумісна.

Для сумісних систем лінійних рівнянь можливі такі випадки:

1. Якщо ранг сумісної системи дорівнює кількості невідомих, тобто , то система (1.4) має єдиний розв'язок.

Система (1.4) має квадратну невироджену матрицю порядку і її єдиний розв'язок можна знайти матричним методом чи за формулами Крамера.

2. Якщо ранг сумісної системи менший від числа невідомих, тобто , то система (1.4) має безліч розв’язків. Її можна розв’язати методом Гаусса – методом послідовного виключення невідомих. При цьому розширена матриця системи за допомогою елементарних перетворень зводиться до трапецієподібної.

Вільні невідомих вибираються довільно, а базисні невідомих визначаються єдиним способом через вільні невідомі.

Зразки розв’язування задач

Приклад 1. (Задача 1.1) Розв'язати систему лінійних рівнянь

двома способами:

а) за правилом Крамера;

б) матричним способом.

Розв'язання.

а) Обчислимо визначник матриці системи

.

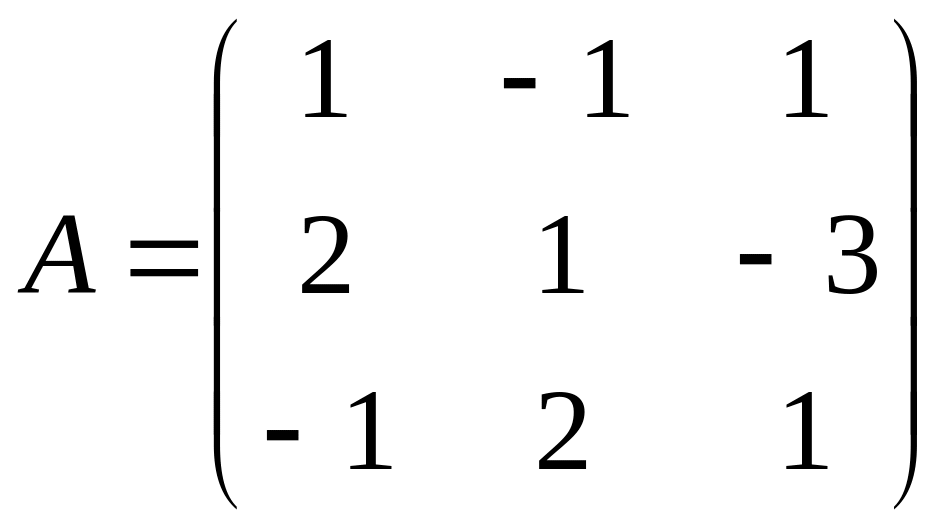Маємо

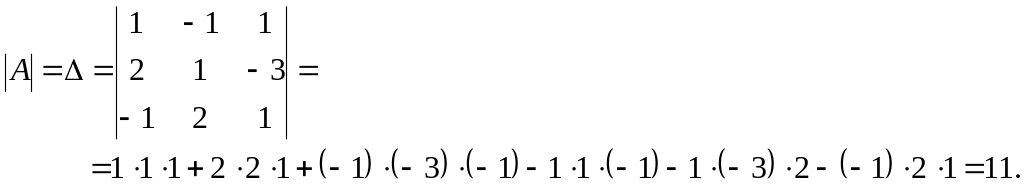
Так як визначник системи , то система має єдиний розв'язок, який можна знайти за формулами Крамера:

.

В цьому прикладі маємо

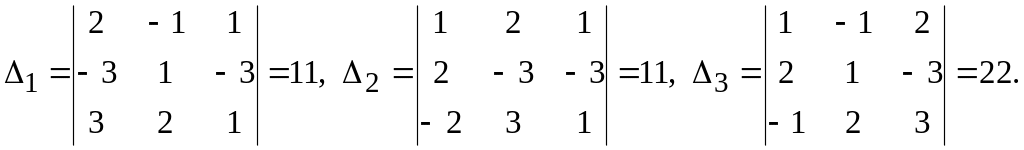
Підставивши знайдені значення визначників у формули Крамера, отримаємо

.

б) Знайдемо розв'язок системи матричним способом.

Дана система рівносильна наступному матричному рівнянню

,

де

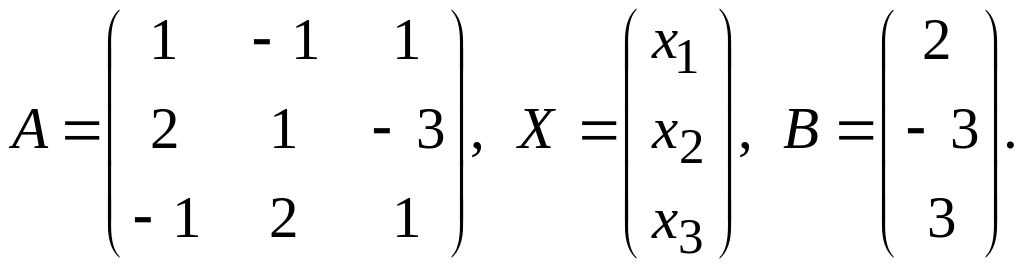
Якщо , то розв'язок системи можна знайти за формулою

,

де – обернена до А матриця, що має вигляд

.

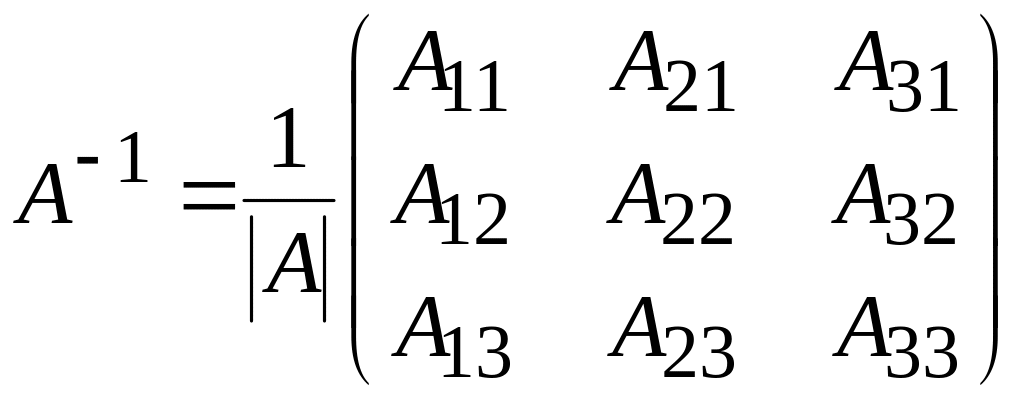Так як , то матриця А має обернену.

Знаходимо матрицю , обернену до А. Обчислимо алгебраїчні доповнення елементів матриці А:

.

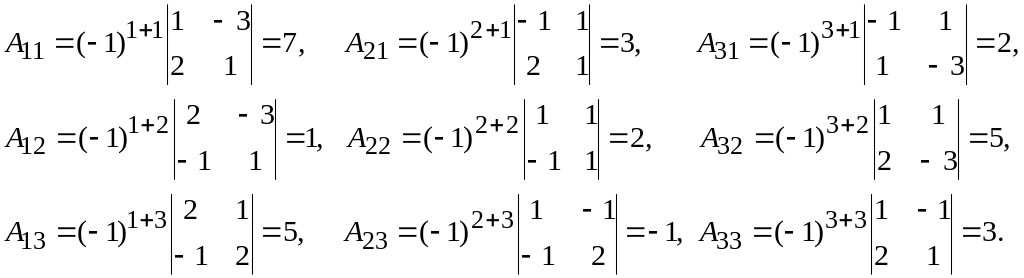
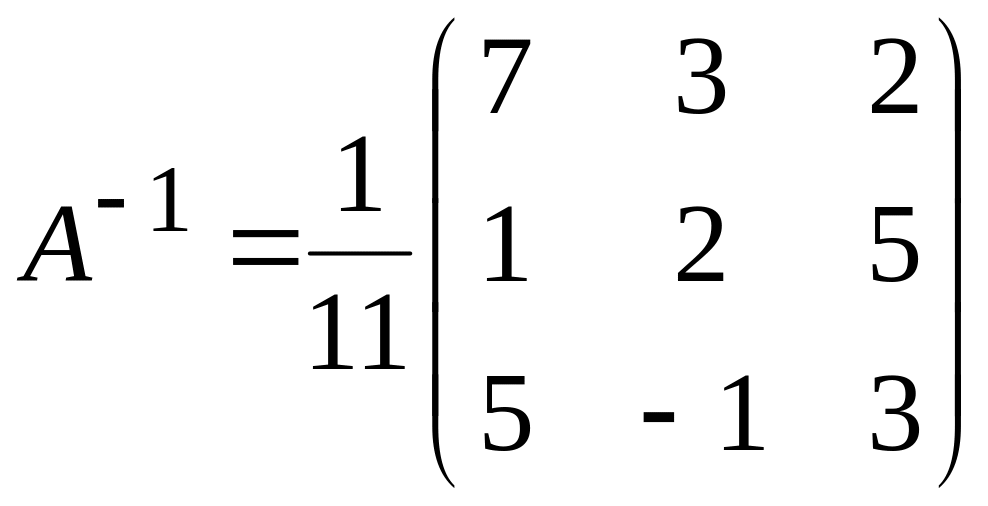Розв'язок системи запишемо за формулою (6) у вигляді:

Звідси .

Приклад 2. (Задача 1.2)

а) Підприємство випускає чотири види виробів П₁, П₂, П₃, П₄ з використанням чотирьох типів сировини S₁, S₂, S₃, S₄. Норми витрат сировини задано матрицею

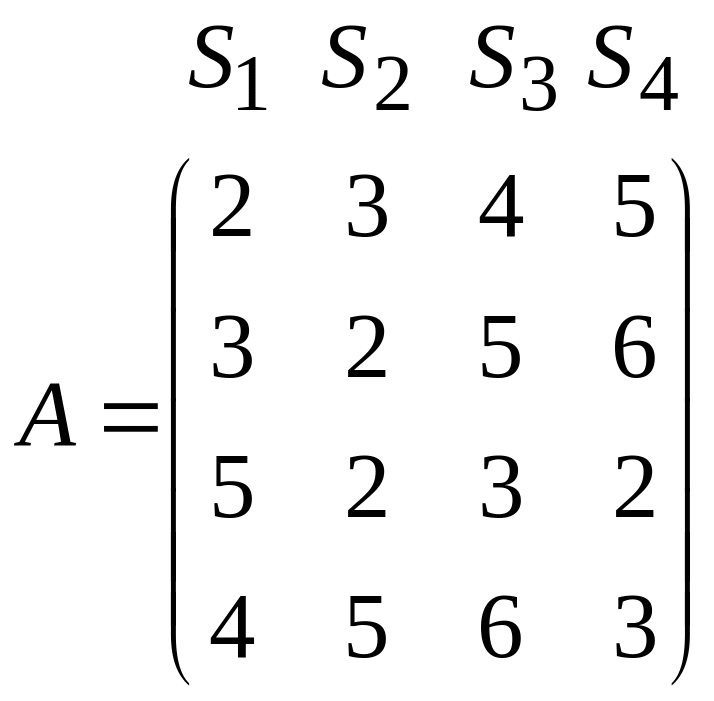
Треба знайти витрати сировини кожного типу при заданому плані випуску кожного виду виробів

.

Розв'язання.

Очевидно, що витрати П сировини кожного типу можна обчислити, користуючись формулою

.

Тоді

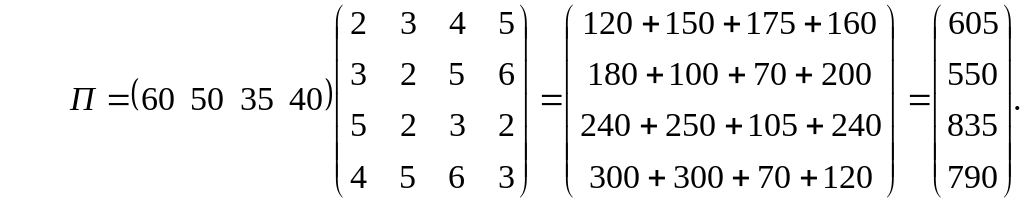
Отже, витрати сировини кожного типу становлять відповідно 605, 550, 835 та 790 одиниць.

б) Взуттєва фабрика спеціалізується з випуску трьох типів продукції П₁, П₂, П₃, використовуючи при цьому сировину трьох видів S₁, S₂, S₃. Норми витрат кожної сировини на одну пару взуття і обсяг витрат сировини на один день задані таблицею 3.

Таблиця 3.

Вид сировини	Витрати сировини на одиницю продукції			Запаси сировини
	П1	П2	П3
S1	6	4	5	2400
S2	4	3	1	1450
S3	5	2	3	1550

Знайти щоденний обсяг випуску кожного типу взуття.

Розв'язання.

Нехай щоденно фабрика випускає пар виробів П₁, пар виробів П₂ і пар виробів П₃. Тоді згідно з витратами сировини кожного виду маємо систему рівнянь

Розв'яжемо дану систему за формулами Крамера:

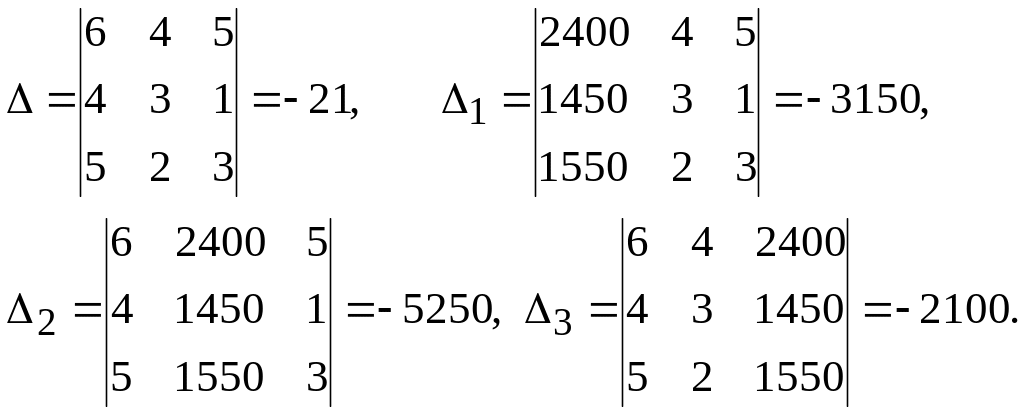
Отже,

,

а це означає, що фабрика випускає 150 пар взуття типу П₁, 250 пар взуття типу П₂ і 100 пар взуття типу П₃.

Приклад 3. (Задача 1.3)

Розв'язати систему лінійних рівнянь методом Гаусса.

Розв'язання.

Маємо

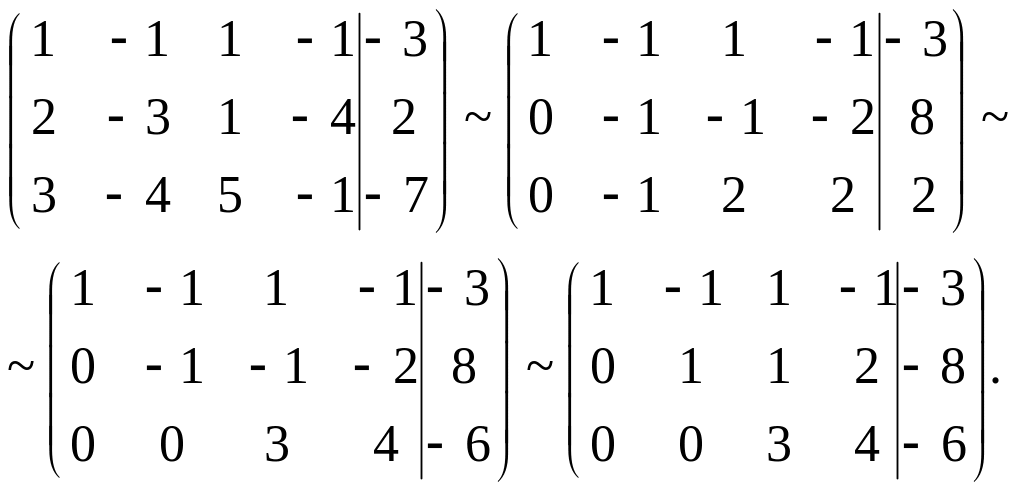
Отже, . Система сумісна. Оскільки ранг менший числа невідомих, то система має безліч розв'язків.

Перетворена система матиме вигляд

або

де – базисні, а – вільна невідома. Розв'язавши останню систему відносно , піднімаючись знизу вгору, знайдемо

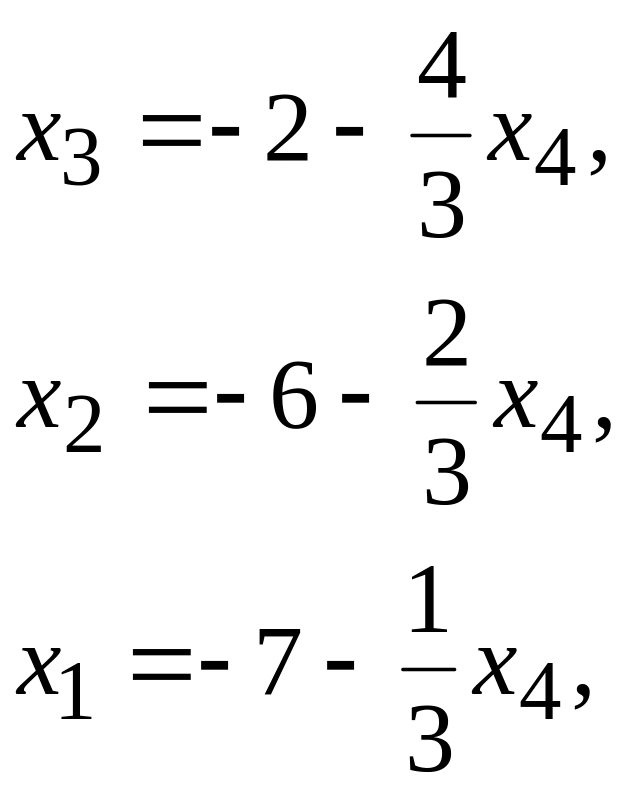
де набуває довільних значень.

Отже, , – розв’язок системи.