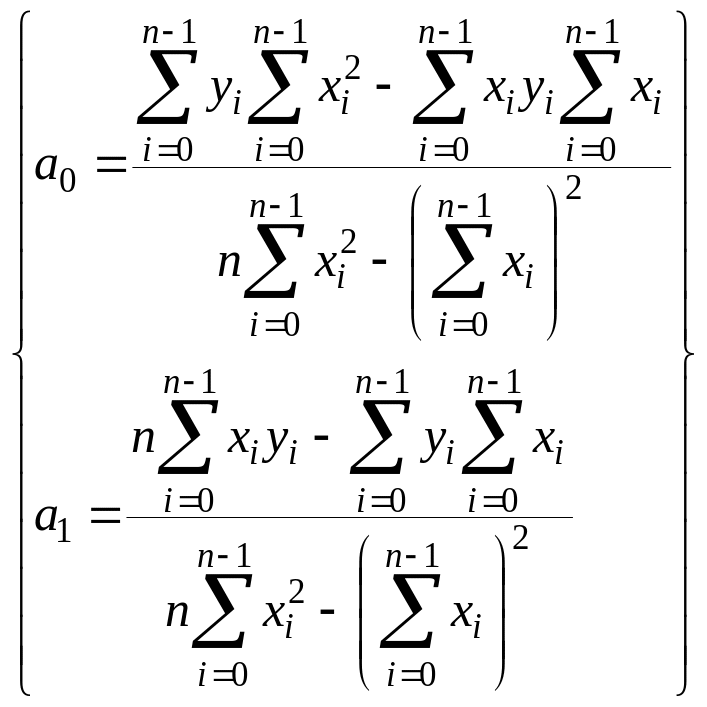7.2. Критерії узгодженості апроксимуючої функції з даними експерименту

Припустимо, що початковими даними апроксимованої функції є використання результатів вимірювань (опиту) її значень

(2.5)

на сітці

(2.6)

і апроксимуюча функція визначається формулою (2.1).

при фіксованому значенні і визначеному виборі базисних функцій

Задача. Як найкраще виконати “узгодження” вектора

з вектором результатів вимірювань шляхом вибору потрібних коефіцієнтів .

Дана постановка задачі отримає конкретний точний зміст після прийняття деякого критерію оптимальної узгодженості векторів та .

На практиці частіше використовують такі два критерії (методи наближення функцій):

• метод коллокації – (інтерполяційне наближення – від лат. interpolatio – “змінювання”; в математиці – визначення проміжних значень величини за деякими відомими її значеннями);

• метод найменших квадратів (МНК).

Метод коллокації – найпростіший метод узгодження функцій та – є проходження графіка функції через експериментальних точок або інакше – рівність векторів та рівносильна системі рівнянь

(2.7)

У матричній формі

,

(2.7а)

де

,

(2.7б)

Виконання умов (2.7) називають колокацією, а узагальнений багаточлен , який задовольняє ці умови, є інтерполяційним багаточленом, тобто багаточленом, що інтерполює функцію на сітці .

Приклад. Дано на сітці . Розглянемо найпростіші базисні функції .

Знайти інтерполяційний багаточлен виду (тобто ).

Розв’язок: система (2.7) має вигляд

,

(2.8)

Тоді багаточлен має вигляд

,

(2.9)

Отриманий багаточлен описує функцію, що вивчається (процес, систему), на проміжку значень сітки: .

Метод найменших квадратів

Постановка задачі. Нехай потрібно вивчити (дослідити) залежність між фізичними величинами та , які зв’язані деякою функціональною залежністю , вид якої невідомий і його потрібно визначити на основі експерименту. Результатами експерименту є обчислені або виміряні значення на сітці .

Оскільки експериментальні дані мають похибки (помилки), то задача ставиться таким чином: так обробити ці дані, щоб залежність між та відображалась з найбільшою точністю, щоб незакономірні помилки (похибки), які пов’язані з експериментом, були максимально згладжені.

Часто МНК називають методом згладжування. Він широко використовується в системах фільтрової обробки інформації, в системах екстраполяції (прогнозування) та ін.

Задача зводиться до визначення рівняння лінії – яка буде виражати реальну (потрібну) залежність. Вигляд лінії виражає вибір апроксимуючого багаточлена:

• лінійний

• степеневий ;

• параболічний ;

• гіперболічний 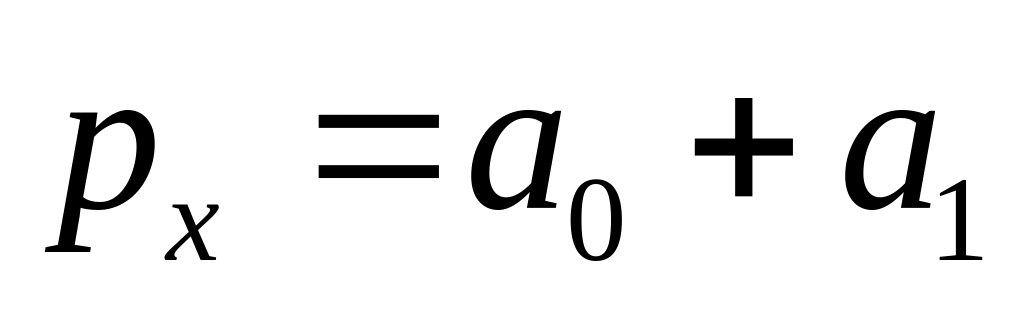тощо.

Нехай це буде лінійна тенденція

.

(2.10)

Підстановка в рівняння (2.10) замість значень дає нам ординати точок прямої, які не збігаються з ординатами точок .Тому різниці між ними

.

Як правило .

Змінюючи параметри і (інакше, вибираючи то одну пряму то другу), можна змінювати величини відхилень , а потім знаходити мінімум суми відхилень (або нев’язок) і визначати коефіцієнти , ; тобто

(2.11)

Однак, даний спосіб супроводжується суттєвим недоліком. Різниці можуть виникати з різними знаками (+ або –).

Тому якщо знаходити суму відхилень у деяких експериментах, то можна отримати малу величину відхилення помилково, за рахунок взаємовилучення складових більшої величини, але різних знаків (рис. 2).

Рис. 2

Уникнути цього недоліку дозволяє міра відхилення (критерій), яка була запропонована французьким математиком Лежандром (і паралельно Гауссом) у 1806 році, – брати суму квадратів відхилень.

Таким чином, метод апроксимації, суть якого є мінімізація суми квадратів нев’язок ( , веде свій початок від праць таких класиків математичної науки, як Лежандр і Гаусс, і називається методом найменших квадратів

(2.12)

Формула читається так: мінімум суми квадратів “нев’язок”.

Одне з можливих узагальнень формули (2.12) – це “ваговий” МНК:

(2.13)

де – дійсні додатні числа (ваговий коефіцієнт). У матричній формі: – матриця вагових коефіцієнтів.

Причина (джерело) появи вагових коефіцієнтів – це неоднакова точність вимірювань, які проводяться в різних точках сітки . Тому вибирають значення тим більше, чим точніше проводилось вимірювання величини .

Для простоти приймемо, що .

Подамо формулу (2.12) у вигляді:

(2.12а)

Таким чином, побудова оптимального апроксимуючого багаточлена зводиться до знаходження коефіцієнтів, які мінімізують функцію , тобто

(2.14)

(аргумент, що мінімізує функцію ), ─ мірний простір.

Як відомо з курсу математичного аналізу, необхідною умовою екстремуму (функції декількох змінних) є обернення в нуль її частинних похідних у цих змінних:

(2.15)

Розглянемо задачу обчислення коефіцієнтів а_к для полінома першого степеня (лінійна функція ): .

Підставляємо значення у формулу (2.12):

(2.16)

Запишемо систему частинних похідних і прирівняємо їх до нуля:

(2.17)

Розкриваємо дужки у формулі (2.16):

Підставимо у систему (2.17):

; ; ; . ; ; ; .

У результаті отримуємо систему рівнянь:

(2.18)

Для зручності можна ввести позначення

Розв’язуючи систему (2.18) відносно а₀ та а₁, маємо

(2.19)

або після підстановки

(2.20)

Після обчислення коефіцієнти і отримують конкретні числові значення, які підставляються в апроксимуючий багаточлен .

Таким чином, методика оцінки результатів експериментів за допомогою МНК складається з етапів:

І. Обирають апроксимуючу функцію .

ІІ. Визначають , як тобто знаходять систему частинних похідних і прирівнюють їх до нуля.

ІІІ. Розв’язують систему рівнянь відносно коефіцієнтів .

ІV. Записують апроксимуючий поліном з урахуванням числових значень коефіцієнтів .

Кількість лінійних рівнянь повинна бути не меншою за кількість незалежних коефіцієнтів. При цьому чим більше вимірювань, тобто чим більшою мірою система перевизначена (надлишок інформації), тим краще, бо тоді випадкові помилки (похибки) окремих вимірювань вилучають одна одну і рішення стає більш достовірним, тобто багаточлен Р(х) більш адекватно описує систему або процес, що вивчається.