2.4.5. Плоские потенциальные течения

несжимаемой жидкости

Рассмотрим безвихревое движение жидкости в плоскости . Так как для потенциальных течений , то и, согласно (2.12б),

или . (2.95)

Равенство (2.95) означает, что двучлен , где − полный дифференциал некоторой функции , т. е.

,

откуда следует

; . (2.96)

Подставляя выражения (2.96) в уравнение (2.25), получим для плоского течения

.

Таким образом, функция удовлетворяет уравнению Лапласа и называется потенциалом скорости.

Из уравнения линии тока (2.4) следует, что есть полный дифференциал некоторой функции , так что

;

; . (2.97)

Подставив выражения (2.97) в уравнение (2.25), получим уравнение Лапласа:

.

Функция называется функцией тока. Если функция описывает поле скоростей только безвихревого течения, то функция справедлива для любых течений.

Сравнивая выражения (2.96) и (2.97), запишем

; . (2.98)

Уравнения (2.98) называются уравнениями Коши–Римана.

Перемножив уравнения (2.98) крест накрест, получим

. (2.99)

Уравнение (2.99) выражает условие ортогональности линий и , т. е. эквипотенциальные линии и образуют взаимно ортогональную систему.

Функции, для которых выполняются условия (2.98) на комплексной плоскости, могут быть представлены в виде зависимости только от одной комплексной переменной. Такие функции называются комплексным потенциалом, где , . Их особенностью является то, что их действительная часть равна потенциалу скорости, а мнимая − функции тока:

. (2.100)

Рассмотрим несколько конкретных задач, решение которых связано с использованием функции (2.100).

Плоскопараллельные течения. Наиболее простым видом комплексного потенциала является уравнение

, где .

Если , то , , .

Уравнение при − вертикальная линия; (при ) − горизонтальная линия (рис. 2.24).

Рис. 2.24. Схема плоскопараллельного течения

Таким образом, имеет место течение вдоль оси со скоростью .

Течение от диполя:

; ,

где − момент диполя.

В этом случае имеем

; .

Уравнение линии тока , тогда

, или ,

т. е. получается уравнение семейства окружностей.

Уравнение линии постоянного потенциала () имеет аналогичный вид:

.

Графически течение от диполя показано на рис. 2.25.

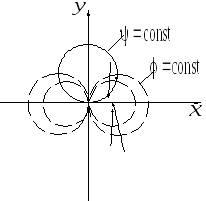
Рис. 2.25. Схема течения от диполя

Обтекание круглого цилиндра. Это течение можно получить наложением плоскопараллельного течения на диполь:

.

Потенциал скорости и функция тока:

,

.

Уравнение линии тока имеет вид . Для нулевой линии тока . В результате получим два уравнения:

и .

Второе уравнение представляет собой уравнение окружности радиусом

.

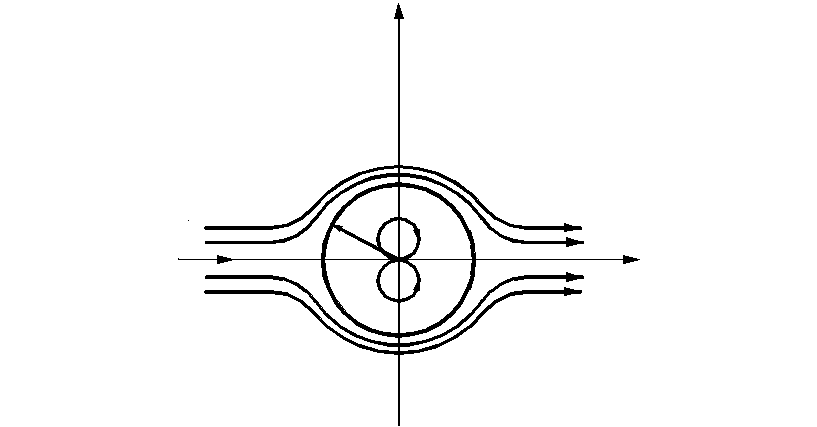
При движении идеальной жидкости любая линия тока может быть заменена твердой стенкой. В нашем случае замена нулевой линии тока твердой стенкой дает картину обтекания потоком круглого цилиндра. Для определения профиля скорости и давления на поверхности цилиндра представим потенциал скорости в цилиндрических координатах (рис. 2.26):

; ; ; ;

;

;

.

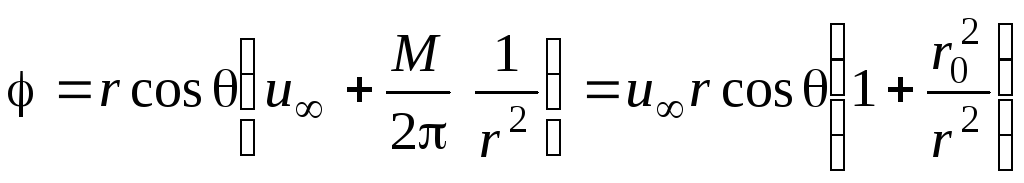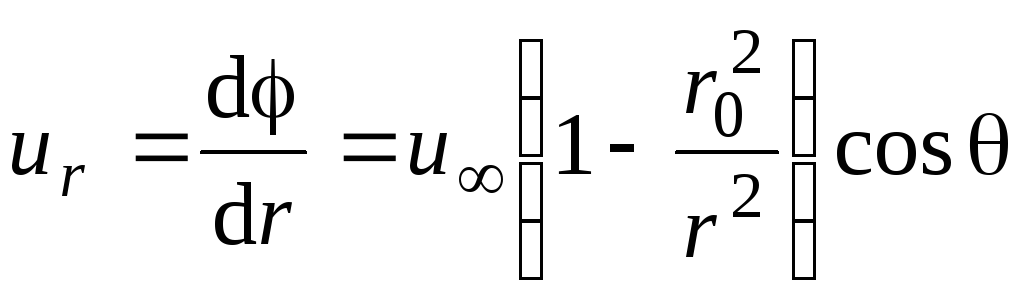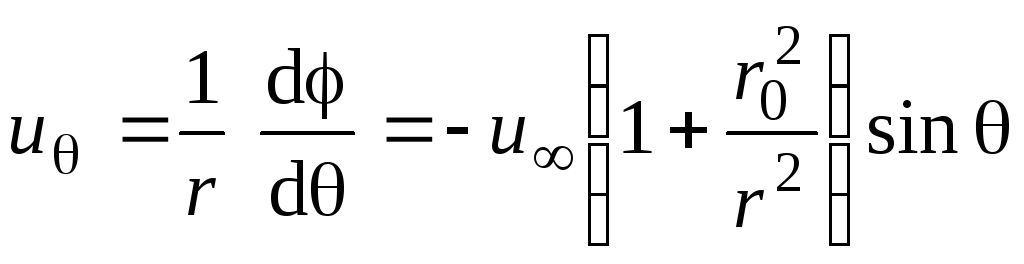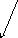
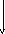
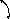
Рис. 2.26. Схема обтекания цилиндра без циркуляции скорости

По поверхности цилиндра , , поэтому

,

при и .

Точки, в которых скорость равна нулю, называются критическими: А − первая критическая точка, В − вторая.

Запишем уравнение Бернулли для нулевой линии и найдем распределение давления по поверхности цилиндра:

; .

Безразмерный коэффициент давления

. (2.101)

На поверхности , тогда

или . (2.102)

При , равном и , ; при , равном и , . Из уравнения (2.45) легко найти значения углов , при которых .

Таким образом, при обтекании цилиндра потенциальным потоком идеальной жидкости распределение давлений и скоростей симметрично относительно осей координат, а это значит, что силы взаимодействия между потоком и цилиндром отсутствуют. Для доказательства этого вывода определим силу давления потока на цилиндр:

,

где и – проекции силы на координатные оси,

;

(2.103)

,

здесь – элементарная площадка, – ширина цилиндра; – длина элемента образующей цилиндра.

Из уравнений (2.101) и (2.102) следует, что давление в любой точке цилиндра

.

Подставив данное значение в уравнение (2.103), запишем

; (2.104)

. (2.104)

Так как , то из равенств (2.104) следует .

Отсутствие силы сопротивления при обтекании тел потенциальным потоком идеальной жидкости называется парадоксом Даламбера.

Результат выполненного решения справедлив только для идеального потока жидкости. Для реальной жидкости симметрия распределения давления по поверхности цилиндра относительно оси ординат нарушается, вследствие чего появляется сила сопротивления (трения) .

Для того чтобы не равнялась нулю, необходимо нарушить симметричность распределения скоростей относительно оси абсцисс. Такое возможно при наличии циркуляции скорости по контуру образующей цилиндра.

Циркуляционное обтекание цилиндра. При наличии циркуляции потенциал скорости и функция тока записываются в следующем виде:

;

.

При

; . (2.105)

Добавление циркуляции скорости изменяет распределение скорости и давления у поверхности цилиндра и смещает критические точки. При получим из уравнений (2.105) (рис. 2.27).

а б в

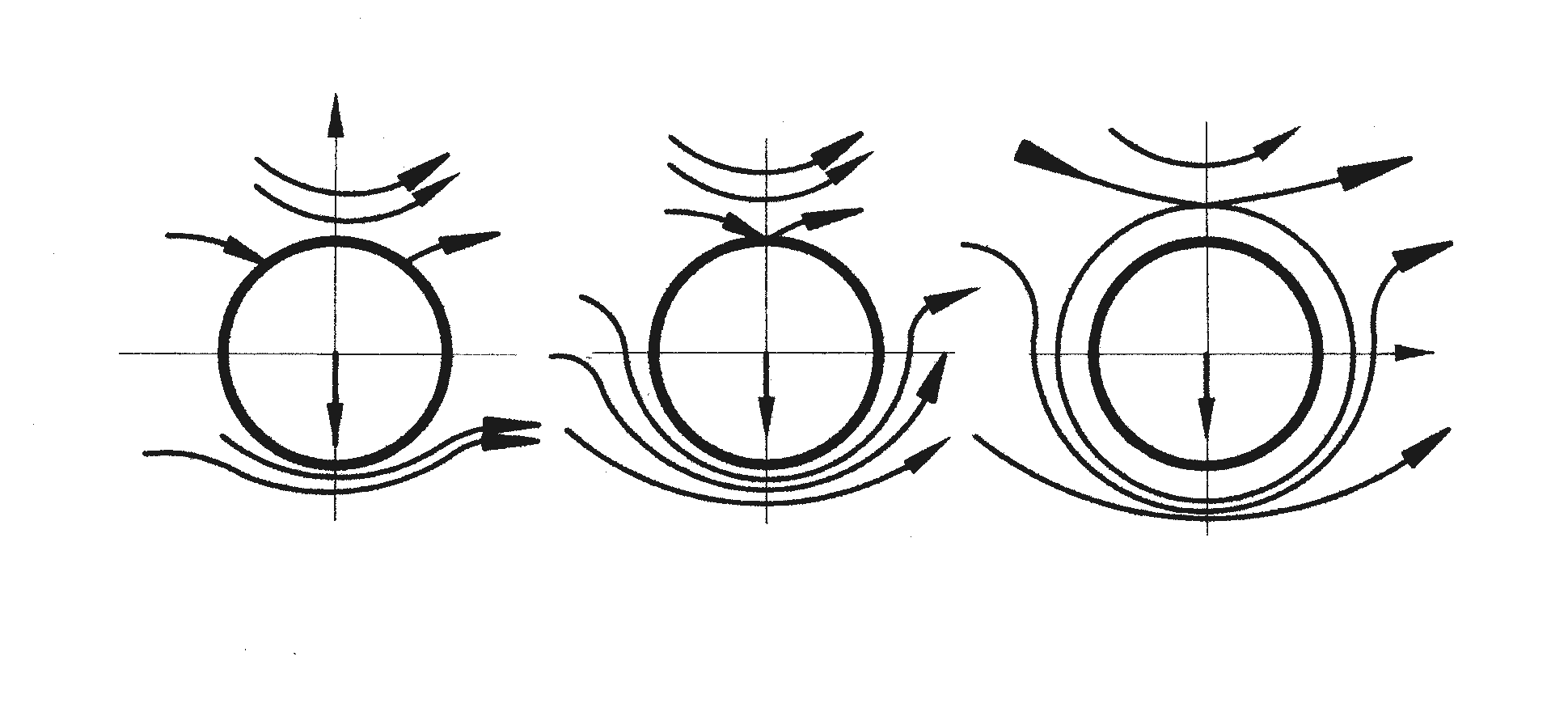
Рис. 2.27. Схема обтекания цилиндра с циркуляцией скорости:

а – ; б – ; в –

В случаях «а» и «б» критические точки находятся на поверхности. В случае «в» точки А и В на поверхности не находятся и вокруг цилиндра образуется течение. Наличие циркуляционного течения нарушает осесимметричность потока относительно оси , в результате чего появляется вертикальная сила . В гидромеханике принято вычислять не саму силу, а величину силы, отнесенную к ширине цилиндра и имеющую размерность ньютон на метр (Н/м). Тогда из уравнения (2.103) получим

. (2.106)

Сила , как и в предыдущем случае, равна нулю.

Давление найдем из уравнения Бернулли для нулевой линии:

, или .

Подставив в данное равенство уравнение (2.105), получим

. (2.107)

После интегрирования уравнения (2.106) совместно с уравнением (2.107) следует

.

Так как , то окончательно имеем

. (2.108)

Появление силы можно объяснить, основываясь на уравнении Бернулли, согласно которому статическое давление меньше в той части потока, где скорость наибольшая. На рис. 2.27 видно, что скорость обтекания цилиндра жидкостью наибольшая в нижней его части (линии тока сжаты), значит, давление там наименьшее. Этот факт и определяет величину и направление силы взаимодействия цилиндра и потока.

Уравнение (2.108) является частным случаем теоремы Н.Е. Жуковского о подъемной силе.