2.1.2. Деформационное и вращательное
движение жидкости
В начале данного раздела отмечалось, что при движении элемент жидкости претерпевает линейные и угловые деформации. Определим, какими величинами они характеризуются.
Линейная деформация. Рассмотрим
движение элемента жидкости в виде
отрезка 0А вдоль оси 0x
(рис. 2.2). Пусть за время dt
точка переместится из положения A
в положение A1.
При этом приращение длины отрезка
составит
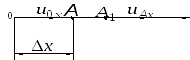
Рис. 2.2. Линейная деформация элемента жидкости
Для бесконечно малого отрезка
имеем
тогда
Скорость относите-льного удлинения
отрезка
,
или скорость относительной линейной
деформации вдоль оси
,
Аналогично для остальных осей
. (2.6)
Таким образом, частные производные от составляющих скорости по одноименным координатам есть скорости относительных линейных деформаций элемента жидкости вдоль координатных осей.
Угловая деформация. Деформация
может происходить по всем координатам.
Выделим в жидкости элемент в виде отрезка
длиной dx,
ориентированного вдоль оси 0x
(рис. 2.3) в плоскости x0z.
За время dt
он из положения
переместится в положение A1B1,
при этом происходят его угловая и
линейная деформации
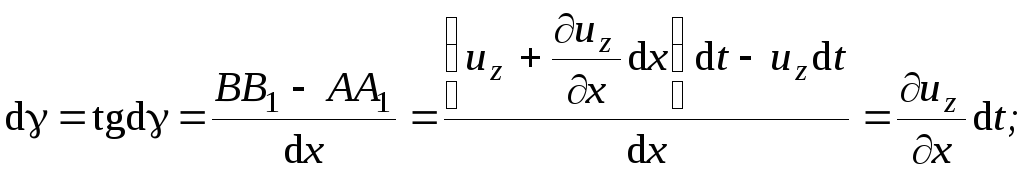
откуда
(2.7)
Рис. 2.3. Угловая деформация элемента жидкости
Аналогичным образом можно получить
следующие скорости угловых деформаций
в плоскостях
,
и
:
(2.8)
Следовательно, производные от составляющих скоростей по разноименным координатам есть скорости относительных угловых деформаций элемента жидкости, или его угловые скорости вращения относительно осей координат.
Из выражения (2.8) видно, что первые две
производные – это угловые скорости
вращения бесконечно малого отрезка
относительно оси 0
,
вторые – относительно оси 0
и третьи – относительно
оси 0
.
Вихревое движение жидкости. При
движении жидкости можно наблюдать
образование вихрей (например, при встрече
с препятствиями). Рассмотрим движение
элемента жидкости, имеющего проекцию
на плоскость
в виде прямоугольника 0ABC (рис. 2.4).
За время
прямоугольник повернется и деформируется
таким образом, что точка A переместится
в положение
,
– в положение
и т. д.
Рис. 2.4. Линейная и угловая деформации
элементарного объема жидкости
Согласно уравнению (2.7) и рис. 2.4,
Суммарная угловая деформация элемента жидкости
Скоростью угловой деформации в плоскости
принято называть величину
(2.9)
Подставляя в равенство (2.9) значения
,
запишем
(2.10)
Аналогичным образом можно выразить
скорости угловых деформаций в плоскости
и
:
(2.10а)
(2.10б)
Из девяти скалярных величин угловых деформаций можно составить матрицу, называемую тензором скоростей деформаций:
.
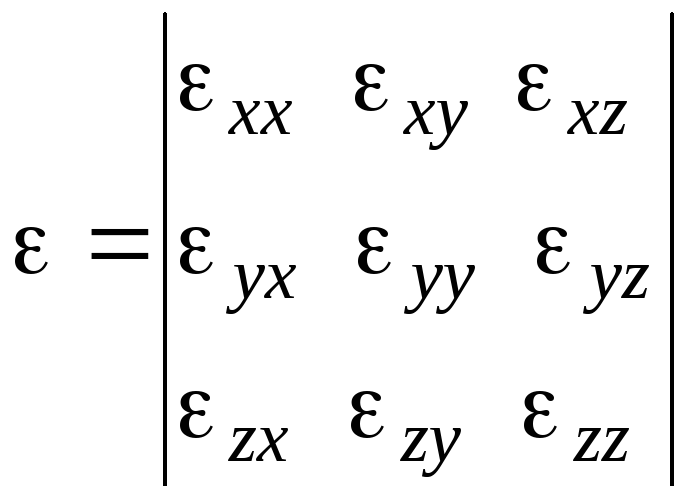(2.11)
Средний угол поворота
Тогда угловая скорость вращения элемента
жидкости относительно оси 0
(2.12)
Аналогичным образом можно записать
величины
и
:
(2.12а)
(2.12б)
Выражение в скобках обозначается
.
Так как
то
(2.13)
Для безвихревого движения
Вихревая линия – линия, в каждой
точке которой вектор угловой скорости
направлен по касательной к ней. В этом
случае
,
из этого следует уравнение вихревой
линии
(2.14)
Трубка тока, элементарная струйка. Поверхность, образованная линиями тока, проведенными через точки произвольного контура, называется трубкой тока.
Трубка тока бесконечно малого сечения, заполненная линиями тока, называется элементарной струйкой.
Сечение, нормальное к линиям тока, называется «живым» сечением. Скорость по сечению элементарной струйки ввиду малости ее живого сечения постоянна и равна локальной скорости.
Расход жидкости через сечение элементарной
струйки может быть определен следующим
образом. За время
через живое сечение
элементарной струйки (рис. 2.5) проходит
объем жидкости
.
Так как
,
то
.
Величина элементарного объемного
расхода
определяется в виде
и, следовательно,
(2.15)
Тогда объемный расход жидкости через живое сечение потока, состоящего из бесконечно большого множества элементарных струек,
(2.16)
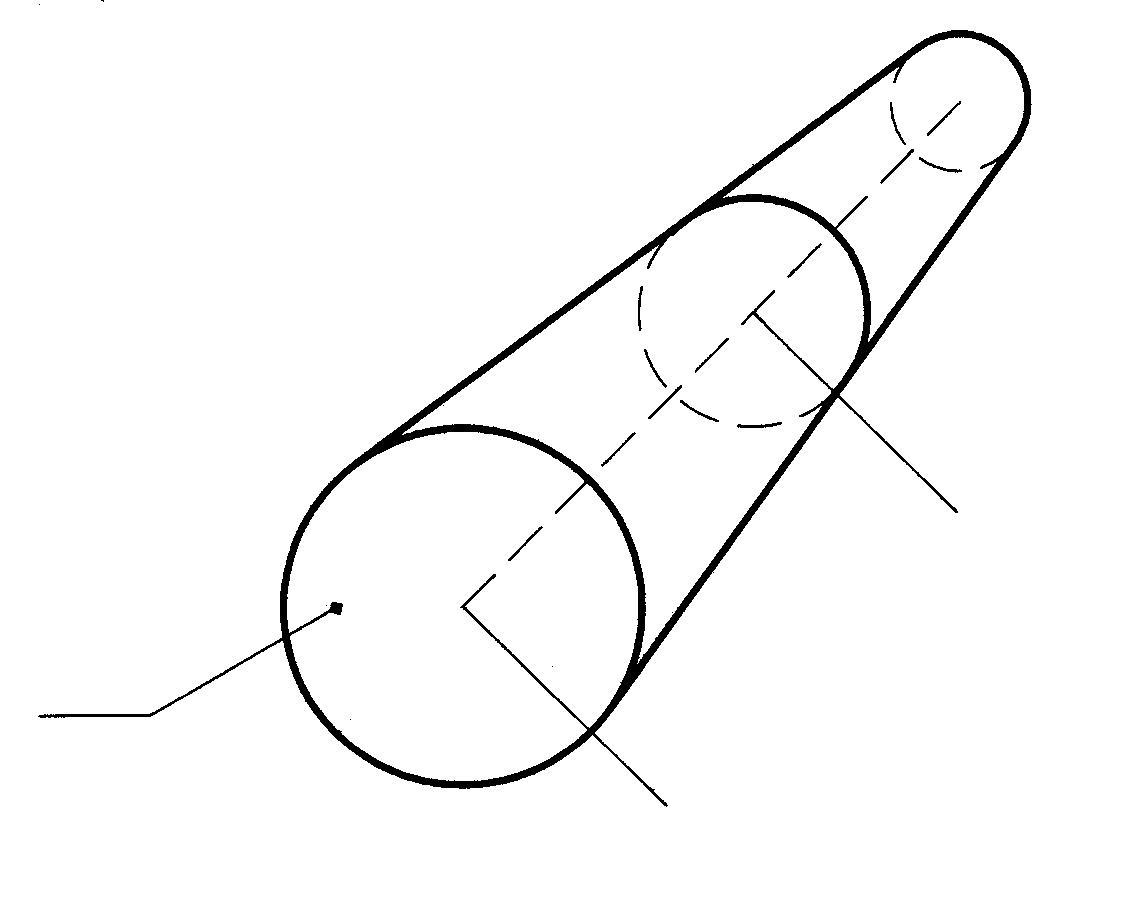
Рис. 2.5. Элементарная струйка жидкости
Модель, согласно которой поток представляется в виде системы бесконечно большого количества элементарных струек, называется струйной моделью потока. При этом постулируется, что боковая поверхность каждой струйки является непроницаемой для среды, движущейся в соседних с ней струйках.
Средняя скорость потока
где
– массовый расход, кг/с; он связан с
объемным расходом следующим образом:
Для среды с изменяющейся плотностью
(2.17)
для несжимаемой жидкости
и
(2.17а)
Равенства (2.17) и (2.17а) называют законом сплошности или законом постоянства расхода для потока. В них индексы 1 и 2 соответствуют двум произвольно выбранным по длине потока живым сечениям. Аналогичным образом можно записать закон постоянства расхода для любого числа выбранных живых сечений.
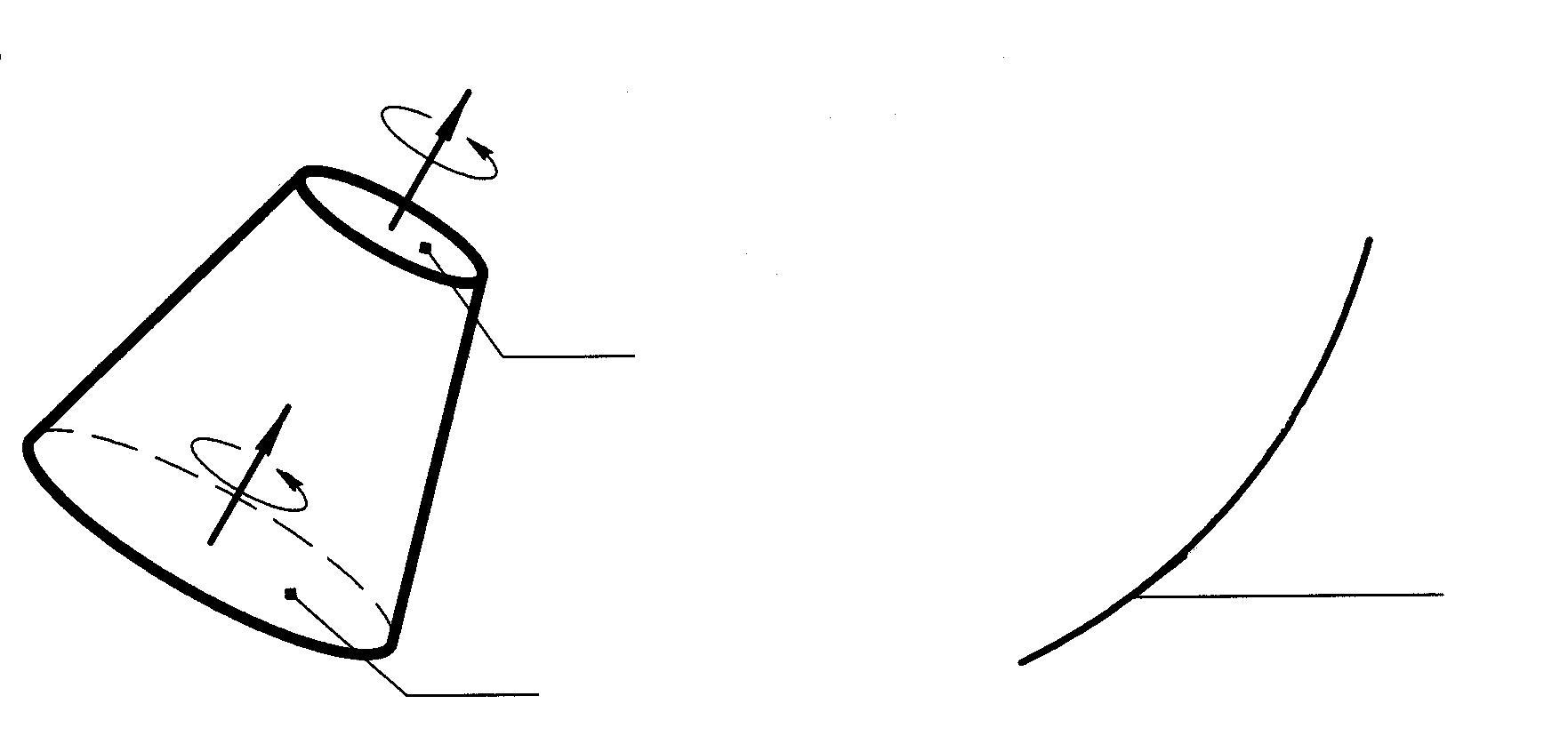
Поверхность, образованная вихревыми
линиями, называется вихpевой трубкой
(рис. 2.6). Для вихревой трубки справедливо
равенство
Из этого равенства следует, что сечение
вихревой трубки не может быть равным
нулю, так как
не может равняться бесконечности.
Циркуляция скорости. Циркуляцией скорости Г по контуру на участке AB (рис. 2.7) называется криволинейный интеграл
Циркуляция по замкнутому контуру
(2.18)
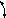
Рис. 2.6. Вихревая трубка тока Рис. 2.7. Схема к определению
циркуляции скорости по контуру
Вопросы для самоконтроля
1. В чем заключаются различия в задании движения элемента жидкости по Лагранжу и Эйлеру?
2. Запишите уравнения ускорения движения жидкости в векторной форме и в проекциях на координатные оси. Дайте физическое толкование слагаемых этих уравнений.
3. Дайте определения линии тока и траектории движения. Когда они совпадают?
4. Выразите среднюю скорость через локальную.