2.5.5. Основное уравнение равномерного движения
Равномерным называется установившееся
движение с постоянной по величине и
направлению скоростью. Исходя из этого
рассмотрим случай движения жидкости
по каналу постоянного живого сечения
имеющего смоченный периметр П и
расположенного под углом
к горизонту (рис. 2.31).
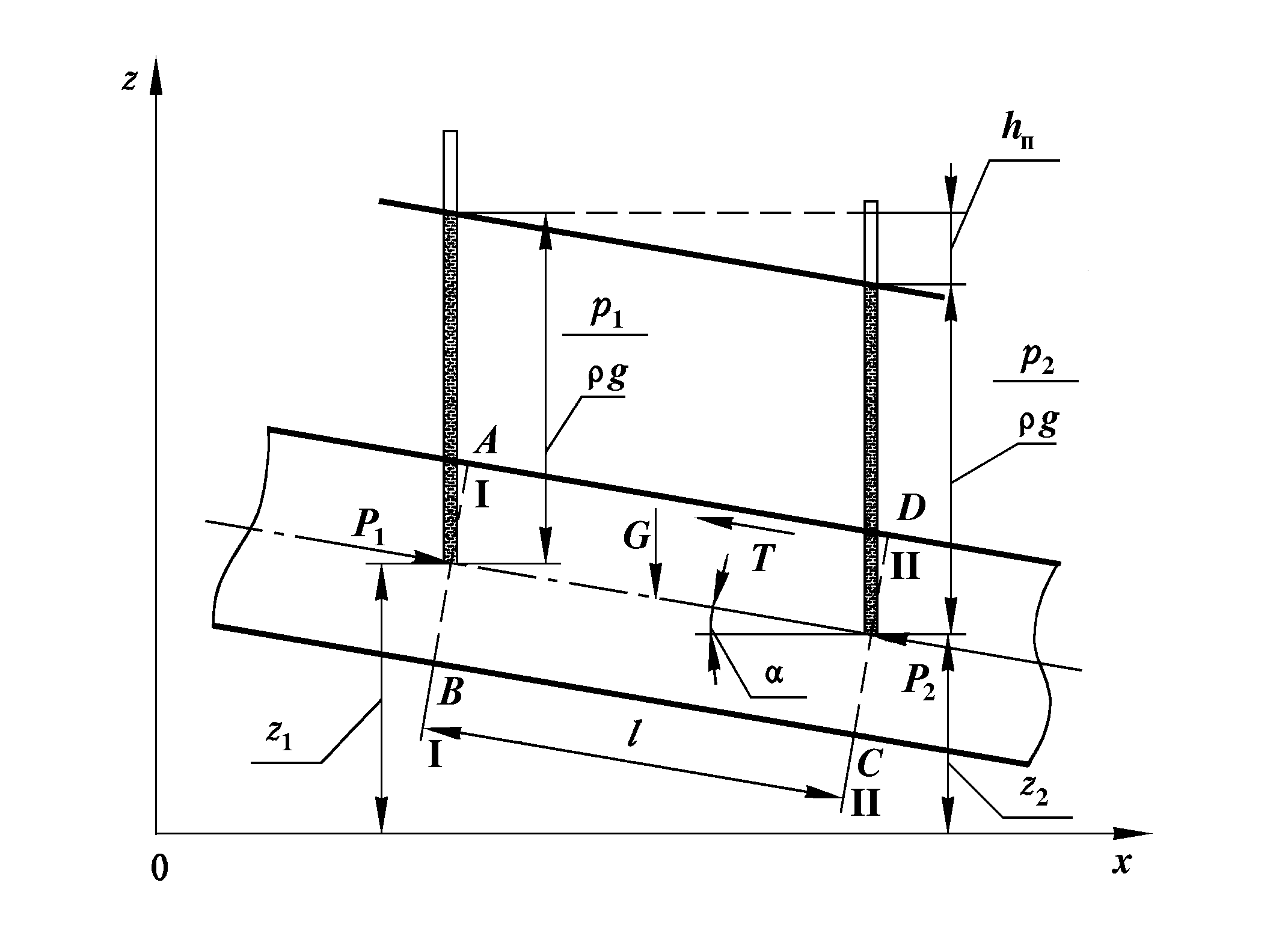
Рис. 2.31. Схема равномерного движения потока жидкости
Проведя живые сечения I–I
и II–II на
расстоянии
друг от друга, выделим объем жидкости
ABCD. Внешними силами, воздействующими
на него, являются силы давления
и сила тяжести
где
– давления в центрах тяжести сечений
I–I и II–II
(им отвечают пьезометрические высоты
).
Действию этих сил оказывают сопротивление силы внутреннего трения в жидкости и силы трения жидкости о стенки трубопровода. Суммарный эффект этих сил сопротивления можно определить в виде общей силы сопротивления
,
где
– касательное напряжение.
Проецируя указанные выше силы на продольную ось канала, имеем
С учетом того, что
запишем
. (2.135)
Разделив левую и правую части уравнения
(2.135) на
получим
(2.136)
Средние скорости
и
в живых сечениях I–I
и II–II
одинаковые, поэтому формула (2.136)
приобретает вид
(2.137)
В соответствии с уравнением Бернулли
для реальной жидкости, левая часть
формулы (2.137) определяет потери по длине
трубопровода на участке
(см. рис. 2.31). Отсюда получаем
(2.138)
Зависимость (2.138) называется основным уравнением равномерного движения. Оно справедливо как для напорного движения, так и для безнапорного движения в открытых каналах.
Преобразуем зависимость (2.138), вводя в
нее эквивалентный диаметр
и величину
В результате основное уравнение
равномерного движения принимает вид
(2.139)
Уравнение (2.139) устанавливает связь между перепадом давления по длине канала и касательным напряжением.
Вопросы для самоконтроля
1. Какие режимы движения вы знаете, в чем их различия?
2. В чем заключается гидродинамическое подобие потоков? Ка-кие критерии гидродинамического подобия вы знаете? Объясните их физический смысл.
3. Напишите уравнение Бернулли для реальной жидкости. В чем различие уравнений Бернулли для элементарной струйки и потока жидкости?
4. Какие виды потерь вы знаете, как они рассчитываются?
5. Дайте определение равномерного движения.
6. Какая связь существует между касательными напряжениями и перепадом давления?
2.5.6. Ламинаpные течения
Задачи, связанные с нахождением параметров потока жидкости при ламинарном режиме течения, могут быть решены точно на основе уравнения Навье–Стокса с некоторыми упрощающими допущениями.
Рассмотрим плоское установившееся
напорное течение несжимаемой жидкости
вдоль оси 0х со скоростью
Так как
массовыми силами можно пренебречь,
т. е.
Согласно уравнению сплошности (2.23),
уравнение (2.46) примет вид
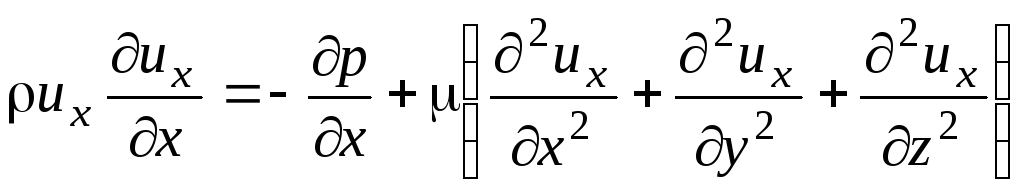. (2.140)
Уравнение (2.140) называется уравнением слоистых течений. На основе данного уравнения решим несколько частных задач.
Течение в плоском канале
Рассмотpим равномерное движение жидкости вдоль оси 0x в канале, обpазованном двумя паpаллельными пластинами (pис. 2.32).
Из уравнения неразрывности потока
(2.23) следует
Упростим задачу, введя понятие бесконечной
шиpины канала, удовлетвоpяющей условию
В этом случае можно cчитать,
что боковые стенки не будут влиять на
характер движения жидкости и
.
С учетом принятых допущений, имея в
виду, что градиент скорости по оси
отрицателен, из уравнения (2.140) следует
(2.141)
а б
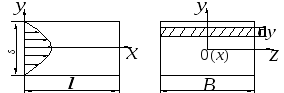
Рис. 2.32. Схема плоского канала:
а – продольное сечение; б – поперечное сечение
Согласно уравнению Бернулли (2.128), падение
давления в канале на участке длиной
происходит линейно, тогда от отношения
бесконечно малых величин можно перейти
к отношению конечных:
.
Подставляя значение
в выражение (2.141), запишем
. (2.142)
Наша задача заключается в нахождении уравнения, описывающего профиль скорости по сечению потока. С этой целью проинтегрируем уравнение (2.142) дважды.
После первого интегрирования получаем
.
Постоянную интегрирования
находим из условий на оси канала
и
.
В итоге
.
После второго интегрирования
Постоянную интегрирования
находим, приняв второе граничное условие
на стенке при
.
С учетом значения
окончательно имеем
(2.143)
Таким образом, при ламинарном режиме течения профиль скорости по сечению потока имеет вид квадратичной параболы (см. рис. 2.32).
Расход жидкости через живое сечение
канала находим по уравнению (2.16). Так
как
,
то
.
Решая интегpал, найдем
(2.144)
Поскольку
,
где
,
то из pавенства (2.144) сле-дует
(2.145)
Определим максимальную скорость из
уравнения (2.143) при
и сравним ее со средней скоростью:
Таким образом, максимальная скорость в плоском канале в полтора раза больше средней.
Решая уpавнение (2.145) относительно
Так как
,
то после несложных пpеобpазований получим
(2.146)
Обозначив в равенстве (2.146) отношение
, (2.147)
окончательно запишем
(2.148)
Уpавнение (2.148) называется уравнением
Даpси–Вейсбаха и используется для
pасчета потеpь давления по длине.
Коэффициент
называют коэффициентом Даpси или
коэффициентом гидравлического трения.
Разделив обе части равенства (2.148) на
,
приведем его к виду
(2.148а)
Уравнение (2.148а) определяет потери удельной энергии по длине канала (энергии, отнесенной к единице веса жидкости) и также называется зависимостью Дарси–Вейсбаха.