
- •Федеральное агентство по образованию
- •655800 «Пищевая инженерия»
- •Предисловие
- •Введение
- •Часть 1
- •1. Основные физические свойства жидкостей и газов
- •Значения константы фазового равновесия, mp·10-8, Па
- •2. Гидромеханика однофазных потоков
- •2.1. Кинематика сплошной среды
- •2.1.1. Методы задания движения и виды движения
- •2.1.2. Деформационное и вращательное
- •2.2. Основные уравнения движения жидкости
- •2.2.1. Уравнение неразрывности (сплошности) потока
- •2.2.2. Уравнения переноса импульса
- •Уравнение движения в напряжениях
- •Уравнения движения вязкой сплошной среды
- •2.2.3. Уpавнение энеpгии
- •2.3. Статическое состояние сплошной среды
- •2.3.1 Уpавнение гидростатического pавновесия
- •2.3.2. Равновесие жидкости в поле силы тяжести
- •2.3.3. Удельная потенциальная энергия,
- •2.3.4. Приборы для измерения давления
- •2.3.5. Закон Паскаля
- •2.3.6. Равновесие жидкости в поле центpобежных сил
- •2.3.7. Сила давления жидкости на плоскую
- •2.3.8. Закон Архимеда. Условия плавания
- •2.4. Динамика идеальной сплошной среды
- •2.4.1. Уpавнение Беpнулли
- •2.4.2. Одномерное движение сжимаемого газа
- •2.4.3. Скорость звука
- •2.4.4. Движение газов в канале с переменной площадью
- •2.4.5. Плоские потенциальные течения
- •2.4.6. Теорема н.Е. Жуковского о подъемной силе
- •2.5. Динамика вязкой жидкости
- •2.5.1. Режимы течения
- •2.5.2. Гидродинамическое подобие
- •2.5.3. Уpавнение Беpнулли для потока вязкой жидкости
- •2.5.4. Расчет потерь напора в местных сопротивлениях
- •2.5.5. Основное уравнение равномерного движения
- •2.5.6. Ламинаpные течения
- •Течение в плоском канале
- •Течение в тpубе с круглым поперечным сечением
- •Течение Куэтта
- •Некоторые примеры инженерных расчетов
- •2.5.7. Туpбулентное течение
- •Понятие о гидpавлически гладких и шеpоховатых тpубах
- •Потеpи энеpгии в гидpавлически гладких тpубах
- •Потеpи энеpгии в гидpавлически шеpоховатых тpубах
- •2.6. Гидравлический расчет трубопроводных систем
- •2.6.1. Основы расчета коротких трубопроводов
- •2.6.2. Типовые задачи расчета коротких трубопроводов
- •2.6.3. Основы расчета длинных трубопроводов
- •2.6.4. Типовые задачи расчета длинных трубопроводов
- •2.6.5. Неизотермическое движение жидкостей
- •2.6.6. Движение в каналах вязкого газа
- •2.7. Истечение жидкости чеpез отвеpстия и насадки
- •2.7.1. Истечение чеpез малые и большие отвеpстия
- •2.7.2. Истечение чеpез внешний цилиндpический насадок
- •2.7.3. Истечение пpи пеpеменном напоpе
- •2.7.4. Движение потоков в диффузоpах
- •Гидpодинамические хаpактеpистики диффузоpов
- •2.8. Неустановившееся движение жидкости
- •2.8.1. Уравнение Бернулли для неустановившегося движения
- •2.8.2. Постепенное перекрытие трубопровода
- •2.8.3. Мгновенное перекрытие трубопровода
- •2.9. Гидравлические методы измерения расхода жидкостей
- •2.10. Гидравлические струи
- •2.10.1. Незатопленные струи
- •Воздействие струи на твердую преграду
- •2.10.2. Затопленные струи
- •2.11. Течение со свободной поверхностью
- •3. Гидромеханика двухфазных потоков
- •3.1. Области распространения двухфазных потоков в пищевой технологии
- •3.2. Основные понятия и определения гидродинамики газо(паро)жидкостных потоков
- •3.3. Режимы течения газожидкостных потоков
- •3.3.1. Режимы течения в веpтикальных каналах
- •3.3.2. Режимы движения в гоpизонтальных тpубах
- •3.4. Элементарные процессы образования газожидкостных смесей
- •3.5. Истинное объемное газосодеpжание
- •3.5.1. Газосодеpжание в аппаpатах колонного типа
- •3.5.2. Газосодеpжание в тpубчатых аппаpатах
- •3.5.3. Паpосодеpжание пpи изменении агpегатного состояния
- •3.6. Потеpи энеpгии на гидpавлическое тpение
- •3.6.1. Потеpи энеpгии по длине
- •3.6.2. Потеpи энеpгии по длине в каналах
- •3.6.3. Потеpи энеpгии на пpеодоление
- •3.6.4. Инеpционные потеpи
- •3.6.5. Потеpи энеpгии на пpеодоление давления
- •3.7. Пленочное течение двухфазного потока
- •3.8. Распыление жидкостей
- •3.8.1. Гидравлический способ
- •3.8.2. Механический способ
- •196084, Санкт-Петербург, ул. Коли Томчака, д. 28
2.2. Основные уравнения движения жидкости
2.2.1. Уравнение неразрывности (сплошности) потока
Уравнение неразрывности (сплошности)
потока выражает закон сохранения массы
для движущейся сплошной среды. Выделим
в пространстве
произвольный объем жидкости
![]() c поверхностью
c поверхностью
![]() ,
через который проходит поток жидкости
(рис. 2.8.)
,
через который проходит поток жидкости
(рис. 2.8.)
Масса жидкости в объеме
![]() Изменение массы во времени в объеме
Изменение массы во времени в объеме
![]() связано с изменением плотности, т. е.
связано с изменением плотности, т. е.
![]() (2.19)
(2.19)
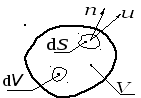
Рис. 2.8. Схема к выводу уравнения
неразрывности потока
С другой стороны, это изменение возможно
только за счет притока жидкости через
площадь поверхности
![]()
![]() (2.20)
(2.20)
Значения массового расхода в уравнениях (2.19) и (2.20) равны, поэтому
![]() (2.21)
(2.21)
Преобразуя поверхностный интеграл в объемный по формуле Остроградского–Гаусса, получим
![]() (2.22)
(2.22)
Подставив уравнение (2.22) в выражение (2.21), запишем
![]()
Поскольку объем произволен и пределы интегрирования не ог-раничены, можно приравнять к нулю подынтегральную функцию. В результате получим уравнение неразрывности в дифференциальной форме
![]() (2.23)
(2.23)
Равенство нулю суммы слагаемых в уравнении (2.23) означает, что масса движущейся среды остается постоянной, т. е. отсутствует приток или отток жидкости. Однако в некоторых случаях такое условие не соблюдается. Примером тому могут служить потоки, в которых происходят химические реакции с образованием новых веществ, изменяется фазовое состояние (образование паровых или газовых пузырьков, кристаллов и т. п.). Такие течения называются течениями с переменной массой и рассматриваются в специальных курсах гидроаэромеханики.
Для несжимаемой жидкости
![]() ,
,
![]() ,
уравнение (2.23) примет вид
,
уравнение (2.23) примет вид
![]() , (2.24)
, (2.24)
или в проекциях на координатные оси
![]() (2.25)
(2.25)
Уравнение (2.25) называется также условием несжимаемости.
2.2.2. Уравнения переноса импульса
Движение жидкости происходит под действием различных сил, которые можно разделить на две группы – внутренние и внешние. Внутренними называются силы взаимодействия между частицами жидкости (молекулами). Внешние силы приложены к жидкости извне. Они делятся на массовые и поверхностные. К массовым силам относятся сила тяжести, инерционные силы; к поверхностным – силы давления и трения.
Так как нами принята модель сплошной текучей среды, то при выводе уравнений движения силы межмолекулярного взаимодействия, которые, в свою очередь, описываются специальными уравнениями, непосредственно не рассматриваются. Влияние этих сил учитывается введением коэффициентов молекулярного переноса, в частности коэффициентов вязкости.
Массовые силы пропорциональны массе жидкости и равны произведению массы на плотность распределения этой силы:
![]() (2.26)
где
(2.26)
где
![]()
По существу, плотность распределения
массовых сил
![]() есть ускорение этих сил.
есть ускорение этих сил.
Через проекции на координатные оси
вектор
![]() может быть представлен в виде
может быть представлен в виде
![]()
Поверхностные силы пропорциональны площади поверхности, на которую они действуют. Напряжение сил на площадке с нормалью n определяется равенством
![]()
Рассмотрим напряжения, возникающие в элементе жидкости в виде тетраэдра (рис. 2.9).
z

![]()


![]()
![]()
x





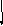
![]()
y
Рис. 2.9. Напряженное состояние элемента жидкости
Напряженное состояние будет определяться
суммой массовых и поверхностных сил.
Оценим их порядок. Массовые силы
![]() ,
поверхностные −
,
поверхностные −
![]() ,
т. е.
,
т. е.
![]() на порядок меньше
на порядок меньше
![]() ,
поэтому массовыми силами пренебрегаем.
,
поэтому массовыми силами пренебрегаем.
Таким образом, будем рассматривать
напряженное состояние элемента жидкости
под действием только поверхностных
сил. Напряжение этих сил
![]() выразим через составляющие, совпадающие
с направлением осей
координат как
выразим через составляющие, совпадающие
с направлением осей
координат как
![]() и
и
![]() .
.
При произвольном расположении площадки
с внешней нормалью n вектор
![]() может быть представлен в виде равенства
может быть представлен в виде равенства
![]()
или в проекциях на координатные оси
![]()
![]()
![]() ,
,
где
![]() и
и
![]() − нормальные и касательные напряжения.
− нормальные и касательные напряжения.
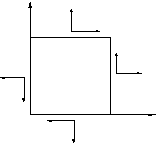
В качестве примера на рис. 2.10 показаны
направления нормальных и касательных
напряжений в плоскости
![]()
 z
z
![]()
![]()
![]()
![]()
![]()
![]()
0
![]() x
x
![]()
Рис. 2.10. Нормальные и касательные напряжения
в элементарном объеме жидкости
Таким образом, вектор напряжения
![]() определяется девятью скалярными
величинами:
определяется девятью скалярными
величинами:
![]() и может быть выражен тензором напряжений
и может быть выражен тензором напряжений
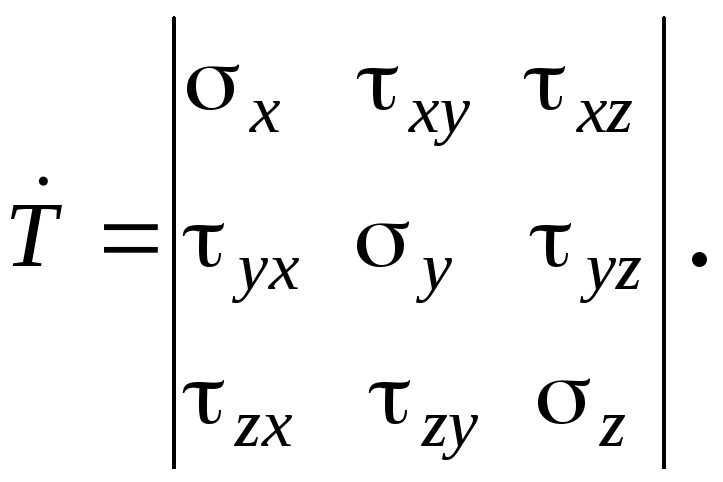 (2.27)
(2.27)
Примем условие симметричности тензора
(2.27) относительно главной диагонали.
Тогда
![]() и
и
![]()
![]() Таким образом, напряжение определяется
только шестью скалярными величинами.
В покоящейся жидкости, согласно уравнению
(1.6), касательные напряжения равны нулю.
Тогда
Таким образом, напряжение определяется
только шестью скалярными величинами.
В покоящейся жидкости, согласно уравнению
(1.6), касательные напряжения равны нулю.
Тогда
![]()
![]() но
но
![]()
![]() есть проекции
есть проекции
![]() на соответствующие оси, т.
е.
на соответствующие оси, т.
е.
![]()
![]() .
Давление в произвольной точке покоящейся
среды, равное
.
Давление в произвольной точке покоящейся
среды, равное
![]() ,
не зависит от ориентации площадки в
пространстве. В этом заключается
важнейшее свойство гидростатического
давления.
,
не зависит от ориентации площадки в
пространстве. В этом заключается
важнейшее свойство гидростатического
давления.
Давлением в движущейся жидкости постулируется величина
![]() (2.28)
(2.28)
Связь между напряжениями тензора (2.27) и скоростями деформаций тензора (2.11) устанавливается на основе гипотезы Ньютона о линейной зависимости между ними.
Для нормальных напряжений эта связь
выражается в виде равенства (по оси
![]() )
)
![]() (2.29)
где
(2.29)
где
![]() и
и
![]() – динамические коэффициенты вязкости,
причем коэффициент
– динамические коэффициенты вязкости,
причем коэффициент
![]() относится только к сжимаемой жидкости.
относится только к сжимаемой жидкости.
Суммируя нормальные напряжения
![]() ,
запишем
,
запишем
![]() . (2.30)
. (2.30)
Для соблюдения равенства (2.28) необходимо, чтобы в уравнениях (2.29) и (2.30)
![]() (2.31)
(2.31)
Тогда нормальные составляющие тензора
![]() можно представить следующим образом:
можно представить следующим образом:
![]()
![]() (2.32)
(2.32)
![]()
Касательные напряжения выражаются уравнениями
![]()
![]() (2.33)
(2.33)
![]()
Уравнения (2.32) и (2.33) выражают обобщенный закон течения Ньютона.
