4. Особенности расчета движения жидкости и газа в слоевых металлургических печах и установках

При анализе технологических процессов в некоторых типах металлургических агрегатов приходится сталкиваться с тем обстоятельством, что использование уравнений, приве­денных в предыдущих главах, сталкивается с определен­ными трудностями. Такие случаи возникают каждый раз, когда металлургическая печь не имеет четко выраженного рабочего пространства, в котором могли бы свободно раз­виваться процессы движения газовых сред, горения топли­ва и теплообмена между газом и обрабатываемыми изде­лиями. В такого рода устройствах материал, подвергаемый переработке, занимает весь объем агрегата в пределах геометрических границ последнего, образуя так называемую пористую среду или слой, чем и объясняется определение: слоевая металлургическая печь (или установка). С тече­нием сквозь пористую среду мы встречаемся, выполняя анализ движения газов и расплавов в доменных печах, агломашинах, воздухонагревателях с шариковой насадкой и др.

Закономерности течения жидкости и газа в слое в зна­чительной степени определяются его (течения) режимом. Для уяснения особенностей газодинамики слоя, а также самого понятия  скорость движения газа в пористой сре­де  рассмотрим случай установившегося ламинарного те­чения с предельно низкими скоростями (ползущее движе­ние). Характерной особенностью стационарного ползущего движения является равенство нулю ускорения потока. Уравнение, описывающее это движение, имеет вид (в про­екции на ось х):

или в векторной форме

(p + h) = ²v = [(v)  (v)]. (12.24)

Здесь использовано известное векторное соотношение:

²v = (v)  (v).

Применим операцию дивергенции к обеим частям урав­нения (12.24). При этом учтем, что дивергенция от ротора непрерывной векторной функции тождественно равна ну­лю, а по уравнению неразрывности для несжимаемой жид­кости v = 0. Тогда получим:

²(p + h) = (²v) = 0. (12.25)

Уравнение (12.25) есть уравнение Лапласа и его реше­ние при заданных граничных условиях дает распределение p + h в пространстве. Ранее мы получили уравнение Лап­ласа для безвихревого движения несжимаемой жидкости, а функция, удовлетворяющая уравнению Лапласа, была названа потенциалом скорости. Ниже мы увидим, что для некоторых потоков вязкой жидкости в качестве потенциала скорости служит величина p + h.

Для удовлетворения уравнения [(p + h)] = 0 в простейших частных случаях достаточно только, чтобы для каждого координатного направления либо p + h, либо (p + h) были постоянными. Мы встречали уже случаи, когда эти условия выполнялись при ламинарном течении. Для этих случаев влияние инерции было равно нулю, и ре­шения уравнений движения показывают, что скорость по­тока пропорциональна градиенту p + h. Например, для те­чения в канале в направлении z средняя скорость

(12.26)

где константа пропорциональности зависит от геометрии поперечного сечения канала.

В отличие от ламинарного течения сквозь трубки посто­янного сечения движение в пористых средах представляет собой ламинарное течение сквозь малые нерегулярные "проходы" в порах среды. С некоторым приближением рас­сматриваемое течение можно уподобить течению в трубах, если только извилистость и переменность сечения каналов учесть поправочным эмпирическим коэффициентом. Тогда по аналогии с уравнением (12.26) для жидкости (или газа при таких малых разностях давления, что его плотность не меняется) можно записать:

(12.27)

В уравнении (12.27) v_z представляет собой скорость филь­трации, определяемую как местную скорость потока, усред­ненную по конечному сечению пористой среды. Это такая скорость, какую имел бы поток в данном месте объема слоя, если бы слоя (пористой среды) не было вовсе. Таким образом, для данной площади поперечного сечения S по­ристого материала, через который протекает расход Q, скорость фильтрации будет:

v = Q/S. (12.28)

Для площади S, конечной (включающей несколько поровых каналов), но достаточно малой, величина v прибли­жается к "локально-осредненному" значению. Применяя в математической теории процесса фильтрации понятие "локально-осредненной скорости", мы представляем тем самым реальную физическую систему, состоящую из сходя­щихся и расходящихся изогнутых струек переменного по­перечного сечения, как некоторый континуум. Иногда ока­зывается полезным понятие средней скорости в порах, оп­ределяемой как

v_ = Q/(S), (12.29)

где пористость (порозность)  представляет собой отноше­ние объема пор (свободного от частиц объема) к общему объему пористой среды.

Коэффициент k₀, называемый коэффициентом проница­емости, имеет размерность квадрата длины. В условиях полного насыщения пор он зависит от геометрии пористо­го пространства и, следовательно, от типа пористой среды, т. е. от величины порозности, формы и расположения пор. Этот коэффициент постоянен, если среда (слой) несжи­маема и изотропна. Для беспорядочно уложенных одно­родных шаров диаметром d (м), продуваемых воздухом, он равен k₀ = 6,1510^-4d² (м²).

Коэффициент фильтрации k определяется соотноше­нием:

k = k₀/ = k₀g/ (12.30)

так что

(12.31)

Коэффициент k имеет размерность скорости, и, если предположить, что выполняются условия полного насыще­ния, зависит от геометрии пористого пространства (типа среды и характеристик пор), а также от удельного веса и вязкости жидкости. Он постоянен для данной жидкости при фикси­рованной температуре, если пористая среда несжимаема и изотропна. Соотношение (12.31) известно как закон Дарси.

Если определить изотропную среду как среду, имеющую одну и ту же проницаемость во всех направлениях, то мож­но написать:

(12.32)

или

(12.32, а)

где v  вектор скорости фильтрации. Применив операцию дивергенции к уравнению (12.32, а) и использовав уравнение:

(12.33)

получаем:

(12.34)

Таким образом, проблема фильтрации сквозь пористые изотропные среды может быть сведена к решению урав­нения Лапласа с соответствующими граничными условия­ми. Если распределение p + h известно, то скорости фильт­рации могут быть получены из закона Дарси в форме (12.32).

В качестве примера использования уравнения (12.34) рассмотрим задачу о движении газов в шахтной печи с фурменным вводом дутья. Здесь в печь прямоугольного по­перечного сечения высотой Н и полутолщиной R через фур­мы диаметром d_ф с противоположных сторон подается газ. Расход газа, поступающего в печь через левую и правую фурмы, различен и соответствует скоростям истечения v₀₁ и v₀₂. Плоскость осей фурм удалена от днища печи на рас­стояние (H₁ + H₂)/2, причем H₂ = H₁ + d_ф. Требуется опре­делить распределение давления и скоростей в объеме слоя, а также выявить зависимость этого распределения от па­раметров фурменного устройства печи и значений входных скоростей v₀₁ и v₀₂.

Для упрощения предположим, что в объеме печи кар­тина течения сохраняется такой же, как и в плоскости, про­ходящей через оси фурм. Тогда для двухмерной задачи можно записать

(12.34,a)

Граничные условия задачи сводятся к заданию расхода дутья на фурмах, давления на выходе из слоя (на уровне засыпи) и к заданию условия газонепроницаемости стенок, т. е. равенства нулю компонента скорости, нормального к стенке:

(12.35,a)

(12.35,б)

(12.35,в)

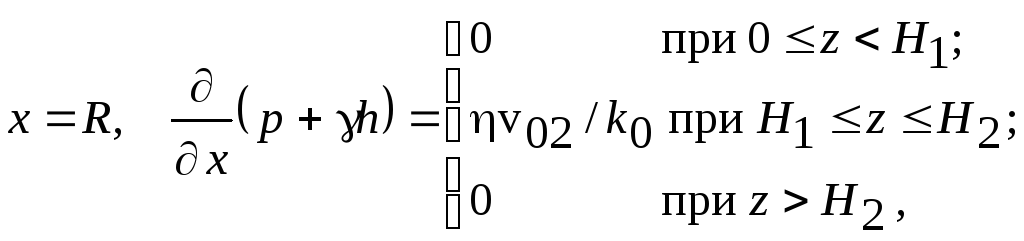(12.35,г)где v₀₁ и v₀₂  абсолютные значения скоростей истечения дутья через фурмы, м/с.

Будем отсчитывать пьезометрическое давление p + h от его значения

на уровне засыпи, т. е.

так как уровень h совпадает с координатой z. Кроме того, неизвестную функцию П(x, z) представим в виде произве­дения двух функций, одна из которых зависит лишь от ко­ординаты х, а другая  координаты z:

(x, z) = X(x)Z(z). (12.36)

Подставив (12.36) в (12.34), находим:

или

(12.36)

Легко узнать в используемом методе черты известного метода разделения переменных. Уравнение (12.36) разделя­ется на два:

(12.36,а)

и

(12.36,б)

Решение уравнения (12.36, а) хорошо известно из курсов физики и теоретической механики (уравнение свободных колебаний системы):

(12.37)

где А₁, А₂  постоянные интегрирования. Используя уравнение (12.35,а), получим:

откуда А₂ = 0. Воспользовавшись соотношением (12.35,6),

получим уравнение для отыскания неизвестной s:

cos(sH) = 0 или s_i = (2i  1)/(2H), (12.38)

где i = 1, 2, 3…

Решение уравнения (12.36,б) также известно и имеет вид:

Здесь В₁, В₂ также постоянные интегрирования. Поскольку уравнение (12.38) имеет бесчисленное коли­чество корней s_i, то общее решение уравнения (12.34, а) за­пишется следующим образом:

П (12.39)

где С_1i = A₁B_1i; C_2i = A₂B_2i. Для отыскания двух неизвестных постоянных мы имеем два граничных условия (12.35, в) и (12.35, г). Воспользовав­шись первым из них, получим:

(z). (12.40)

где F₁(z)  правая часть выражения (12.35, в). Уравнение (12.40) есть ни что иное, как разложение функции F₁(z) в ряд Фурье по собственным функциям задачи. Согласно теории рядов Фурье:

или

(12.41)

так как H₂ – H₁ = d_ф и

Аналогично, используя уравнение (12.35, г), находим:

(12.42)

Отыскав из уравнений (12.41) и (12.42) постоянные C_1i и C_2i и подставив их в уравнение (12.39), находим окончатель­ное решение уравнения (12.34, а) с граничными условиями (12.35) в виде:

(12.43)

Расчеты по уравнению (12.43) показывают (рис. 12.13 – 12.14), что вся об­ласть движения подразделяется на две зоны: зону двух­мерного и зону одномерного течения. В первой из них су­щественны оба компонента скорости как горизонтальный, так и вертикальный. Во второй—основное значение имеет вертикальный компонент скорости; горизонтальный компо­нент пренебрежимо мал. Размеры зоны двухмерного тече­ния являются функцией диаметра фурмы, расстояния фур­мы от днища шахты и размеров слоя. В среднем двухмер­ная зона простирается на (0,5  0,7)D от уровня фурм, где D = 2R.

Вид профилей давления и скоростей определяется соот­ношением скоростей v₀₁ и v₀₂. На рис. 12.13 показаны изобары в шахтной печи высотой Н = 20 м при Н₁ = 2,5 м, Н₂ = 2,7 м, v₀₁ = 50 м/с, v₀₂ = 35 м/с и d_ф = 200 мм. Можно видеть, что в подавляющей части объёма слоя давление постоянно по поперечному сечению печи.

Рис. 12.13. Изобары в шахтной печи (цифры на кривых – давление в ата)

При v₀₁ = v₀₂ профили сим­метричны относительно оси z. При v₀₁ > v₀₂ минимум дав­ления и максимум вертикального компонента скорости расположены в области положительных значений x. В об­щем случае положение этих экстремумов определяется из решения уравнений:

(12.44)

На рис. 12.14 показаны изотахи в прифурменной области, полученные при тех же исходных данных, что и поле давления. Данные этого рисунка подтверждают отмеченные выше параметры области двухмерного течения.

Закон Дарси, представляющий собой линейное соотно­шение между скоростью и градиентом величины p + h и использованный при выводе предыдущих уравнений филь­трационного течения, имеет силу только до тех пор, пока течение остается ламинарным и несущественны эффекты инерции. Для слоя мелких частиц число Рейнольдса можно определить выражением: Re = vd₅₀/, где d₅₀  диаметр ча­стицы, при котором масса всех более мелких частиц со­ставляет 50 % от общей массы образца. Эксперименты с мелкими частицами показали, что Re  10 в качестве верх­него предела применимости закона Дарси. Это предельное число Рейнольдса может быть и большим для крупных частиц. Данные экспериментов с мелкими частицами сви­детельствуют о том, что при числах Re , больших 10, не­смотря на то, что течение еще остается ламинарным, про­исходит отклонение от закона Дарси, обусловленное уско­рениями жидкости, вызывающими инерционные эффекты. Переход от ламинарного течения к турбулентному проис­ходит постепенно в интервале между Re = 60 и Re = 600. Сопротивление течению становится, по-видимому, незави­симым от числа Рейнольдса при Re  1000.

Если искривление потока газа незначительно и по-преж­нему можно пренебрегать конвективными ускорениями, то практически при любом числе Re справедливо соотно­шение:

(12.45)

где d_k  средний диаметр частицы слоя;   коэффициент формы частицы (для сферы  = 1, для куска дробленого агломерата  = 0,3), а q = |v| = =(vv)^1/2.

Уравнение (12.45) носит название уравнения Эргана. Ре­шая его относительно скорости фильтрации, получим:

(12.46)

где (12.47)

Подстановка (12.46) в уравнение неразрывности v = 0 приводит к нелинейному дифференциальному уравнению второго порядка в частных производных:

(12.48)

которое уже не поддается аналитическому решению и мо­жет быть решено только численно, например, с использо­ванием метода конечных разностей.

В том случае, когда условие о малой искривленности потока не выполняется (например, при фурменном вводе дутья в шахтную печь), уравнение Эргана приводит к боль­шим погрешностям в определении параметров течения. В этих условиях необходимо решать полные уравнения дви­жения газа в слое. В векторной форме их можно записать следующим образом:

(12.49)

Здесь v  средняя скорость газа в межкусковом прост­ранстве слоя; _п  просветность слоя (просвет), равная от­ношению площади просветов, доступных для газа, к пло­щади поперечного сечения слоя.

Уравнение неразрывности в данном случае имеет вид:

(12.50)

Отметим, что течения, описывающиеся уравнениями (12.45)  (12.50), уже не являются ползущими.

В общем случае решение задач движения газа в слое даже с помощью ЭВМ чрезвычайно трудоемко. Существен­ное упрощение процедуры решения достигается при ис­пользовании введенных ранее понятий потенциала скоро­сти, функции тока и завихренности потока. Однако затраты времени и усилий на разработку численных моде­лей слоевых металлургических печей и установок (в част­ности, моделей газомеханики слоя) очень быстро окупают­ся, так как эти модели позволяют не только анализировать протекающие в печи процессы, но и дают возможность выйти на решение проблемы оптимизации конструктивных и режим­ных параметров агрегата еще на стадии проектирования.