5. Приближенные методы анализа установившихся пограничных слоев

Точные решения уравнений пограничного слоя, рассмот­ренные ранее, позволяют выявить большую часть элемен­тов структуры пристенной области потока. Во многих случаях такой подробной информации не требуется, а нужно лишь оценить значение той или иной характеристики те­чения.

Отрыв пограничного слоя вызывает существенное уве­личение сопротивления, называемого профильным, в основ­ном вследствие завихренности или турбулентного следа за телом, а также вследствие изменения распределения дав­ления по поверхности тела. Несмотря на то, что профиль­ное сопротивление по величине намного больше вязкого, его очень трудно рассчитать. В этих условиях точное ре­шение уравнений пограничного слоя имеет второстепенное значение. Гораздо важнее суметь точно определить точку отрыва пограничного слоя, чтобы задержать или даже пол­ностью предотвратить отрыв путем оптимизации профиля тела или канала. Для конструкторских разработок требу­ются более быстрые методы расчета, чем методы, рассмот­ренные ранее, несмотря на то, что это быстродействие до­стигалось ценой понижения точности расчета.

Для получения приближенных методов расчета харак­теристик пограничного слоя необходимо отказаться от тре­бования, чтобы дифференциальные уравнения погра­ничного слоя удовлетворялись бы для каждой "частицы" жидкости. Достаточно ограничиться, во-первых, выполнением гранич­ных условий и контурных связей на стенке и при переходе к внешнему течению и, во-вторых, выполнением только суммарного соотношения, получаемого из дифференциаль­ных уравнений пограничного слоя как некоторое среднее по толщине слоя.

Выведем это соотношение сначала для простейшего слу­чая установившегося течения вдоль плоской поверхности, когда  p/ x = 0 (U = const). Для этого проинтегрируем уравнение (7.8) по толщине пограничного слоя

. (7.66)

Рассмотрим правую часть этого выражения. Поскольку , то

.

Но на внешней границе пограничного слоя  u/ y = 0 . С другой стороны известно, что касательное напряжение на стенке равно ₀ = ( u/ y)_{y = 0}. Тогда

(7.67)

Запишем теперь второе слагаемое левой части уравне­ния (7.66) в виде

(7.68)

Здесь использовано соотношение

.

Первое слагаемое в правой части уравнения (7.68) легко интегрируется, т.е.

(7.69)

так как на внешней границе пограничного слоя ,v = v_h , а на стенке u = = v = 0.

Для определения величины v_h, а также для преобразо­вания второго слагаемого правой части выражения (7.68) воспользуемся уравнением неразрывности , тогда

(7.70)

. (7.71)

Таким образом, приходим к интегральному уравнению импульсов, содержащему касательное напряжение на стен­ке ₀:

. (7.72)

При установившемся движении, как уже отмечалось ра­нее, при отсутствии продольного перепада давления , скорость внешнего теченияи, следова­тельно, может быть внесена не только под знак интеграла, но и под знак производной, т.е. уравнение (7.72) может

быть записано в виде

или

. (7.73)

Учитывая выражение (7.23), окончательно получим, что

, (7.74)

где  - толщина потери импульса.

Этому уравнению можно придать другой вид. Если учесть, что коэффициент местного сопротивления трения связан с касательным напряжением на стенке и скоро­стью внешнего течениясоотношением

,

то получим .

Для неустановившегося движения и течение вне пограничного слоя, где влияние вязкости пренебрежи­мо мало, описывается уравнением Эйлера (7.12), а уравне­ние пограничного слоя имеет вид (7.13). Интегрируя послед­нее уравнение по толщине пограничного слоя, находим

. (7.75)

Поскольку ине зависят от, то с учетом уравнений (7.67  - 7.71) можно записать

. (7.76)

Запишем третье слагаемое левой части этого выражения в виде

так как иU₁, U₁/ x не зависят от y.

Следовательно, имеем

или с учетом выражений (7.21) и (7.23)

(7.77)

Интегральное уравнение импульсов впервые было вы­ведено Т. Карманом. Уравнения (7.73), (7.74) и их обобще­ние—выражение (7.77) - часто называются интегральны­ми уравнениями (теоремами) импульсов Кармана.

Заметим, что при выполнении оценки порядка величин, сделанной при выводе уравнений Прандтля (7.8), а следо­вательно, и интегрального уравнения импульсов (7.77), вклад турбулентных флуктуации не учитывался. Тем не ме­нее, интегральное уравнение импульсов (7.77) используется как при ламинарном движении, так и при турбулентном. Это допустимо до тех пор, пока поток количества движе­ния, обусловленный турбулентностью, мал по сравнению с потоком количества движения, обусловленным скоростями осредненного течения. При несоблюдении данного условия следует пользоваться более точным выражением, получен­ным из уравнений турбулентного пограничного слоя

.

Полагают, что последнее слагаемое левой части этого урав­нения может быть существенным вблизи точки отрыва.

Необходимо отметить, что интегральные уравнения по­граничного слоя (интегральные уравнения импульсов) сами по себе являются точными, хотя бы в рамках теории погра­ничного слоя. Приближенный характер решений этих урав­нений обусловлен способом их применения.

Рассмотрим общий случай установившегося движения в пограничном слое. Перепишем уравнение (7.77) следующим образом

, (7.78)

или

. (7.79)

Если выбрать для распределения скоростей необходи­мое выражение и с его помощью вычислить толщину вы­теснения, толщину потери импульсов и касательное напря­жение на стенке, то получим из уравнения (7.78) обыкно­венное дифференциальное уравнение для определения тол­щины пограничного слоя. С целью выбора необходимого выражения для профиля скорости введем вместо размерно­го расстояния от стенки безразмерное расстояние₁ = y/(x). Предположим также, что относительная скорость является функцией₁. Далее, с учетом граничных условий для распределения скоростей u функция f(₁) = u/U₁ дол­жна исчезать на стенке и должна быть равна 1 для больших значений ₁. Хотя все точные решения урав­нений пограничного слоя показывают, что переход погра­ничного слоя в потенциальное течение происходит асимп­тотически (при ₁  ), тем не менее, для приближенного решения целесообразно произвести смыкание пограничного слоя с потенциальным течением на конечном расстоянии от стенки, следовательно, ввести в расчет конечную толщину пограничного слоя (x).

В общем случае, когда вдоль обтекаемой стенки имеет­ся градиент давления, следует предусмотреть, что профили скоростей могут быть как без точки перегиба (прямой пе­репад давления), так и с точкой перегиба (обратный пере­пад). Далее, для того, чтобы приближенный расчет мог дать также положение точки отрыва необходимо преду­смотреть выполнение условия , т.е. возмож­ность существования профиля скорости, имеющего на стен­ке касательную, совпадающую с нормалью к стенке.

Преимущество интегрального метода состоит в том, что окончательное решение слабо зависит от формы профиля скорости. Обычно профиль выбирают так, чтобы можно было удовлетворить как можно большему числу граничных условий.

Пусть течение в пограничном слое стационарно и, следовательно, . Тогда, учитывая равенство, из уравнения (7.79) получим уравнение (7.74) в виде

. (7.80)

Выберем профиль скорости в виде кубической параболы

. (7.81)

Согласно условию прилипания при , отсюда. Далее, из выражения (7.63) следует, что при. Тогда, т.е.и вместо уравнения (7.81) можно записать:

. (7.82)

Для отыскания двух коэффициентов имеем два условия: . Используя их, получаем:и. Следовательно

. (7.83)

Подставив в выражение (7.78) в (7.23), находим

.

Таким образом, вместо уравнения (263) имеем

или .

Интегрируя это уравнение при граничном условии приx = 0, получаем или

. (7.84)

Сопоставив это уравнение и уравнение для толщины пограничного слоя, находим, что интегральный метод дает ошибку в определении , равную 7,2%.

Располагая значением , вычисляем , т.е. , что всего лишь на 2,7% отличается от решения Блазиуса.

В табл. 7.2 приведены результаты решения уравнения (7.80) для различных приближений профилей скоростей — от линейного до синусоидального. Линейная функция удов­летворяет лишь условиям f (0) = 0 и f (1) = 1; кубическая функция — дополнительно двум условиям f’’(1) = 0 и f”’(0) = 0; функция четвертой степени – условию f’’’(1) = 0. Функция sin(₁/2) удовлетворяет тем же граничным ус­ловиям, что и полином четвертой степени, за исключением условия f’’’(1)=0. Можно видеть, что полиномы третьей и четвертой степени, а также функция sin(₁/2) дают для касательного напряжения на стенке значения, отличающи­еся от результатов точного решения не более чем на 3%,. что следует рассматривать как вполне хороший результат. Значения толщины вытеснения ^, даваемые указанными приближениями, также удовлетворительно совпадают с точными значениями.

Таблица 7.2. Результаты приближённого расчёта пограничного слоя плоской пластины, обтекаемой в продольном направлении

u/U1 = f(1)	(Rex)^1/2/ x	^(Rex)^1/2/ x	(Rex)^1/2 /x или cf(Rex)^1/2	Cf(Rel)^1/2	H = ^/
1	3,464	1,732	0,577	1,155	3,00
(31 - 1^3)/2	4,641	1,740	0,646	1,293	2,69
21 - 21^3 + 1^4	5,836	1,751	0,685	1,371	2,56
sin(1/2)	4,795	1,743	0,655	1,310	2,66
Точное решение	5,000	1,721	0,664	1,328	2,59

Переходя к анализу турбулентного пограничного слоя, отметим, что наиболее простое решение задачи можно по­лучить, если использовать степенную форму универсально­го профиля скорости, а не логарифмическую, более при­емлемую в других отношениях. Уже отмечалось, что сте­пенной профиль с показателем 1/7 вполне удовлетворитель­но аппроксимирует опытные данные в диапазоне примерно от 30 до 500 при . Если необходимы данные для больших значений , то исполь­зуют другие степени. Закон одной седьмой степени имеет вид:

или .

Полагая, что при y =  , и решая последнее уравне­ние относительно ₀ (), получаем

₀ = 0,0228 U₁²(U₁/)^1/4. (7.85)

Подставляя степенной закон в уравнения (7.21), (7.23), после интегрирования находим ^/ = 0,125,  = 0,097, от­куда H = ^ = 1,29, и касательное напряжение в уравнении (7.85) можно выразить через толщину потери импульса:

. (7.86)

Тогда вместо уравнения (7.74) запишем ^1/4 d/d x = 0,0128 (/U₁)^1/4.

Если турбулентный слой развивается от передней кром­ки пластины, то граничное условие имеет вид:  = 0 при . Следовательно, (4/5) ^5/4 = = 0,0128 (/U₁)^1/4x или

(7.87)

Вычисление других характеристик пограничного слоя с использованием вышеприведенных данных не вызывает затруднений.

Произвольное изменение скорости внешнего течения

Вернемся к общему случаю решения уравнения (7.79). Ум­ножив его на (U₁) и записав вместо ₀ его значение ( u/ y)_{y = 0} , придадим выражению (7.79) безразмерную форму, т. е.

. (7.88)

Для упрощения алгебраических выкладок введем еще один параметр пограничного слоя — динамическую толщи­ну _д = U₁/( u/ y)_{y = 0}. Кроме того, обозначим T = /_д. Тогда уравнение (7.88) принимает вид:

(7.89)

где  = (²/)(dU₁/d x).

Анализ точных решений уравнений пограничного слоя показал, что функция F() хорошо аппроксимируется ли­нейной зависимостью F() = a   b, причем по данным Твейтса, а = 0,45 и b = 6. После подстановки этого соотношения в (7.89), перегруппировки слагаемых и объединения производных получим уравнение , ин­тегрируя которое поx и учитывая при этом, что одна из величин ( и ) при x = 0 должна быть равна нулю, на­ходим

Приняв указанные Твейтсом значения а и b, оконча­тельно получим

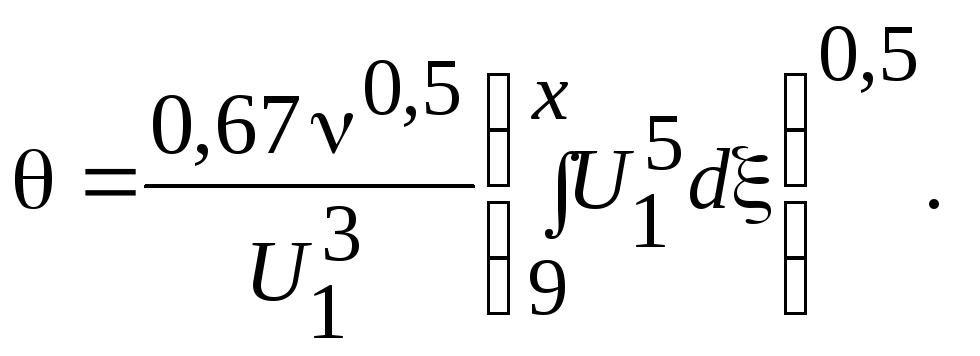(7.90)

Интересно, что при U₁ = const из этого выражения вытекает:  = 0,67 x/Re_x^1/2, что лишь на 0,9 % превышает точное значение.

Определив по уравнению (7.90) толщину потери импуль­са, можно вычислить местный параметр  и затем с по­мощью табл. 7.3, составленной на основании точных реше­ний уравнений пограничного слоя, вычислить динами­ческую толщину, местное касательное напряжение и локальный коэффициент трения.

Таблица 7.3. Функции, используемые с уравнением (7.90)

		H = ^/
 0,082	0	3,70 отрыв пограничного слоя
 0,080	0,039	3,58
 0,070	0,089	3,17
 0,060	0,113	2,99
 0,040	0,153	2,81
 0,024	0,182	2,71
0	0,220	2,60 плоская пластина
0,016	0,244	2,55
0,048	0,291	2,44
0,080	0,333	2,34 критическая точка (приближённо)
0,120	0,382	2,23
0,250	0,500	2,00

В литературе можно найти более точные методы расче­та ламинарного пограничного слоя, которые следует использовать лишь при необходимости особо точных реше­ний. Для инженерного анализа достаточно точности урав­нения (7.90).

Если использовать степенной профиль скорости, то можно получить решение уравнения движения турбулент­ного пограничного слоя при произвольном изменении ско­рости внешнего течения. В этом случае формпараметр оп­ределяется по выражению H = 1 + 2/n. При п = 7 он сохра­няет постоянное значение 1,29 и остается в силе уравнение (7.86). Такой метод расчета можно использовать лишь для течений с отрицательными градиентами давления — пря­мой перепад при движении жидкости (газа) с ускорением, например, при истечении через сопла. При положительных градиентах давления (обратный перепад) он практически бесполезен. Для течений с положительными градиентам» давления разработаны более точные методы, но они связа­ны с громоздкими вычислениями и здесь не рассматрива­ются.

Подставив в уравнение (7.79) Н = 1,29 и ₀ из выраже­ния (7.86), получим

Это уравнение можно преобразовать к виду

Интегрируя это уравнение при граничном условии, со­гласно которому при х = 0 одна из величин ( или U₁) рав­на нулю, и решая его относительно , получаем

(7.91)

Определив зависимость  от x по соотношениям (7.52), можно найти , ^ и .

В настоящее время по теории пограничного слоя имеется весьма обширная научная и учебная литература. Рассмот­ренные в данной главе результаты служат введением в бо­лее строгую и точную теорию и дают возможность самоде­ятельного изучения публикаций. Они важны как в отноше­нии разработки методов расчета сопротивления потока (коэффициентов трения), так и (что не менее важно) про­цессов переноса теплоты и массы с точки зрения описания гидродинамической обстановки и последующего решения задач тепломассообмена.