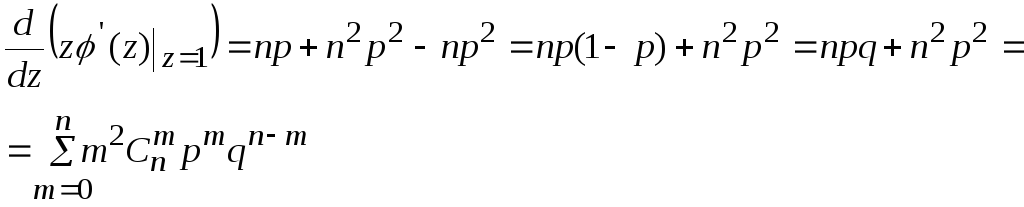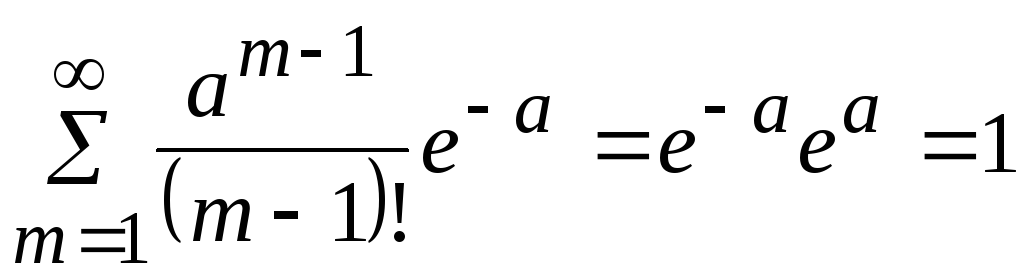- •Теория вероятностей
- •Содержание
- •Раздел 6. Законы распределения функций случайных аргументов. 90
- •1. Теоретическая часть. Введение
- •Раздел 1. Понятие события и его вероятности.
- •1.1. Предмет теории вероятности.
- •1.2. Алгебра событий. Пространство элементарных событий.
- •1.3. Классическое определение вероятности.
- •1.4. Геометрические вероятности.
- •1.5. Частота и вероятность.
- •1.6. Аксиоматическое построение теории вероятностей.
- •1.7. Условная вероятность и простейшие основные формулы.
- •1.8. Формула полной вероятности.
- •1.9 Формула Бейеса.
- •Раздел 2. Последовательные независимые испытания
- •2.1. Независимые испытания. Формулы Бернулли.
- •2.2. Обобщенная теорема о повторении опытов.
- •Раздел 3. Понятие случайной величины. Функция распределения и ее основные свойства.
- •3.1. Понятие случайной величины и функции распределения.
- •3.2. Свойства функции распределения.
- •3.3. Дискретные и непрерывные случайные величины.
- •3.4. Числовые характеристики случайных величин.
- •Раздел 4. Примеры распределений случайных величин.
- •4.1. Биномиальное распределение.
- •4.2. Теорема Пуассона
- •4.3. Закон Пуассона.
- •4.4. Равномерное распределение.
- •4.5. Показательное распределение.
- •4.6.Нормальный закон распределения.
- •Раздел 5. Системы случайных величин (случайные векторы).
- •5.1. Понятие о системе случайных величин.
- •5.2. Функция распределения системы двух случайных величин.
- •5.3. Плотность распределения системы двух случайных величин.
- •5.4. Законы распределения отдельных компонент, входящих в систему. Условные законы распределения.
- •5.5. Зависимые и независимые случайные величины.
- •5.6. Числовые характеристики системы двух случайных величин.
- •5.7. Система произвольного числа случайных величин (случайные вектора).
- •5.8. Числовые характеристики системы нескольких случайных величин.
- •Раздел 6. Законы распределения функций случайных аргументов.
- •6.1. Закон распределения функции одного случайного аргумента.
- •6.2. Закон распределения функции двух случайных величин.
- •6.3. Закон распределения суммы двух случайных величин. Композиция законов распределения.
- •6.4. Распределение произведения.
- •6.5. Распределение квадрата случайной величины.
- •6.6. Распределение частного.
- •6.7. Числовые характеристики функций случайных величин.
- •Раздел 7. Теоремы о числовых характеристиках.
- •7.1. Основные теоремы о математическом ожидании.
- •7.2. Теоремы о дисперсии случайной величины.
- •7.3. Теорема о линейной зависимости случайных величин.
- •Раздел 8. Характеристические функции.
- •8.1. Определение и простейшие свойства характеристических функций.
- •8.2. Предельные теоремы для характеристических функций.
- •Раздел 9. Предельные теоремы для случайных величин.
- •9.1. Сходимость последовательностей случайных величин.
- •9.2. Закон больших чисел.
- •9.3. Следствия закона больших чисел.
- •Раздел 10. Предельные теоремы теории вероятностей.
- •10.1. Центральная предельная теорема.
- •10.2. Теорема Ляпунова.
- •10.3. Теорема Лапласа.
- •2. Практические занятия, тесты, самостоятельная работа. Занятие 1. Непосредственный подсчет вероятности с использованием классического определения вероятности.
- •1.1. Краткая теоретическая часть.
- •1.2. Тест.
- •1.3. Решение типовых задач.
- •1.4. Задачи для самостоятельной работы.
- •Занятие 2. Геометрическое определение вероятности.
- •2.1. Краткая теоретическая часть.
- •2.2. Тест
- •2.3. Решение типовых задач
- •2.4. Задачи для самостоятельной работы
- •Занятие 3. Условная вероятность. Теорема умножения вероятностей.
- •3.1. Краткая теоретическая часть
- •3.2. Тест
- •3.3. Решение типовых задач
- •3.4. Задачи для самостоятельной работы
- •Занятие 4. Теорема сложения вероятностей.
- •4.1. Краткая теоретическая часть
- •4.2. Тест
- •4.3. Решение типовых задач
- •4.4. Задачи для самостоятельной работы
- •Занятие 5. Формула полной вероятности.
- •5.1. Краткая теоретическая часть
- •5.2. Тест.
- •5.3. Решение типовых задач
- •5.4. Задачи для самостоятельной работы
- •Занятие 6. Формула Бейеса.
- •6.1. Краткая теоретическая часть
- •6.2.Тест
- •6.3. Решение типовых задач
- •6.4. Задачи для самостоятельной работы
- •Занятие 7. Последовательные независимые испытания.
- •7.1. Краткая теоретическая часть
- •7.2. Тест
- •7.3. Решение типовых задач
- •7.4. Задачи для самостоятельной работы
- •Занятие 8. Дискретные и непрерывные случайные величины.
- •8.1. Краткая теоретическая часть а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •8.2. Тест
- •А) только к дискретным случайным величинам
- •8.3. Решение типовых задач а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Б) Функция распределения и плотность вероятности непрерывной случайной величины
- •8.4. Задачи для самостоятельной работы а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Занятие 9. Числовые характеристики дискретных случайных величин.
- •9.1. Краткая теоретическая часть
- •9.2. Тест
- •9.3. Решение типовых задач
- •9.4. Задачи для самостоятельной работы
- •Занятие 10. Дискретные и непрерывные случайные величины.
- •10.1. Краткая теоретическая часть
- •10.2. Тест
- •10.3. Решение типовых задач
- •10.4. Задачи для самостоятельной работы
- •Занятие 11. Закон Пуассона.
- •11.1. Краткая теоретическая часть
- •11.2. Тест
- •11.3. Решение типовых задач
- •11.4. Задачи для самостоятельной работы
- •Занятие 12. Закон нормального распределения.
- •12.1. Краткая теоретическая часть
- •12.2. Тест
- •12.3. Решение типовых задач
- •12.4. Задачи для самостоятельной работы
- •Литература
Раздел 4. Примеры распределений случайных величин.
4.1. Биномиальное распределение.
Рассмотрим дискретную случайную величину Х , которая принимает значения 0,1,2,…n с вероятностями
|
|
(4.1.1) |
В схеме Бернулли: Х – число наступлений m раз события А в серии из n – независимых испытаний. Введем в рассмотрение производящую функцию, которая в данном случае имеет вид
|
|
(4.1.2) |
Нетрудно заметить,
что ![]() .
.
Придавая значение Z=1, получим
|
|
(4.1.3) |
Подсчитаем числовые характеристики биномиального распределения:
1) математическое ожидание в соответствии с определением выражается формулой:
|
|
(4.1.4) |
Найдем производную производящей функции:
|
|
(4.1.5) |
Придавая значение Z=1, получим
|
|
(4.1.6) |
Из соотношения (4.1.6) следует
|
|
(4.1.7) |
Далее подсчитаем
дисперсию
![]() по формуле
по формуле![]() .
Второй начальный момент определяется
формулой
.
Второй начальный момент определяется
формулой
|
|
(4.1.5) |
Умножим производную производящей функции на z:
|
|
|
Дифференцируя полученное выражение, получим
|
|
|
и вычисляя при Z=1, получим
|
|
(4.1.6) |
Из (4.1.6) нетрудно
заметить, что
![]() ,
тогда:
,
тогда:
|
|
(4.1.7) |
|
|
(4.1.8) |
Если р–мало, а п–достаточно большое число, то формулой биномиального распределения пользоваться не удобно.
4.2. Теорема Пуассона
Теорема Пуассона.
Если
![]() при
при![]() ,
а
,
а![]() ,
то
,
то
|
|
(4.2.1) |
где
![]()
Доказательство. Очевидно, что


Сомножители начиная
со второго до m-го
и знаменатель последней дроби при
![]() ,
очевидно сходятся к единице. Выражение
,
очевидно сходятся к единице. Выражение![]() отn
не зависит. Числитель дроби
отn
не зависит. Числитель дроби
 при
при![]() сходится
сходится![]() .
Таким образом, предел:
.
Таким образом, предел:
|
|
(4.2.2) |
Что и требовалось доказать.
4.3. Закон Пуассона.
Во многих задачах практики приходится иметь дело со случайными величинами, распределенными по закону, который называется законом Пуассона.
Рассмотрим дискретную случайную величину X, которая может принимать только целые, неотрицательные значения 0,1,2,....m,... причем последовательность этих значений теоретически не ограничена. Случайная величина Х распределена по закону Пуассона, если вероятность того, что она примет определенное значение т, выражается формулой
|
|
(4.3.1) |
где а - некоторая положительная величина, называемая параметром закона Пуассона.
Ряд распределения случайной величины X имеет вид:
Табл.4.3.1.
|
xm |
0 |
1 |
2 |
… |
m |
… |
|
Pm |
e-a |
|
|
… |
|
… |
Убедимся прежде всего, что последовательность вероятностей, задаваемая формулой (4.3.1), представляет собой ряд распределения. Имеем:
|
|
|

На рис. 4.3.1 показаны многоугольники распределения случайной величины X, распределенной по закону Пуассона, соответствующие различным значениям параметра а.
Определим основные характеристики — математическое ожидание и дисперсию — случайной величины Х. По определению математического ожидания
|
|
(4.3.2) |
Первый член суммы (соответствующий m=0) равен нулю, следовательно, суммирование можно начинать с m=1:
|
|
|
Обозначим m-1=k; тогда
|
|
(4.3.3) |
Таким образом, параметр а представляет собой не что иное, как математическое ожидание случайной величины X.
Для определения дисперсии найдем сначала второй начальный момент:
|
|
|
По ранее доказанному
|
|
|
кроме того,
|
|
|
следовательно,
![]() .
.
Далее находим
дисперсию случайной величины X:
![]() .
.
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию а..
Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина Х распределена по закону Пуассона.