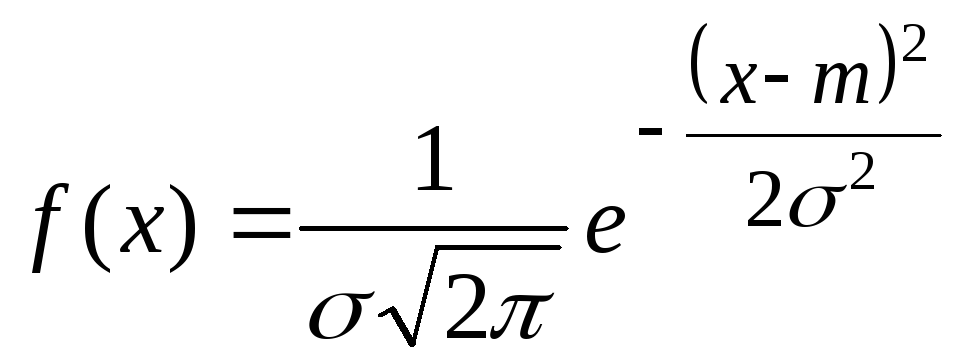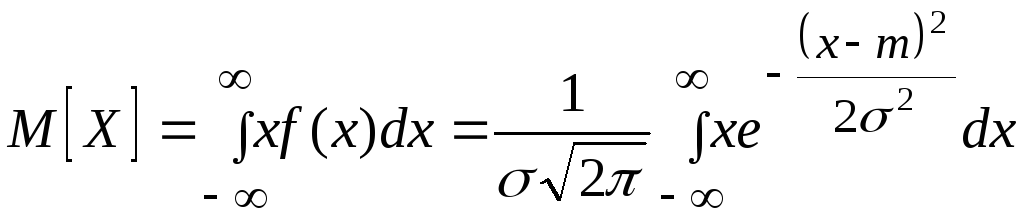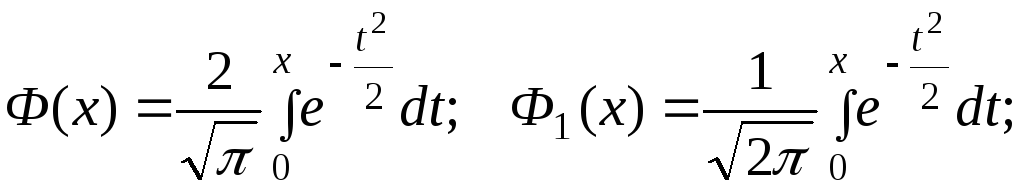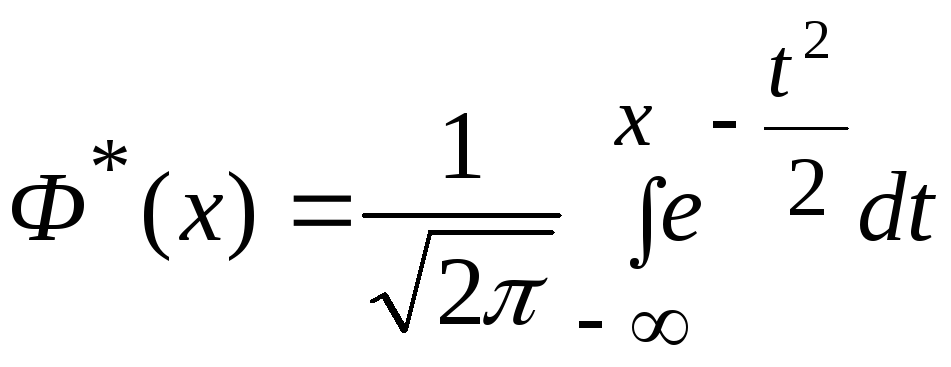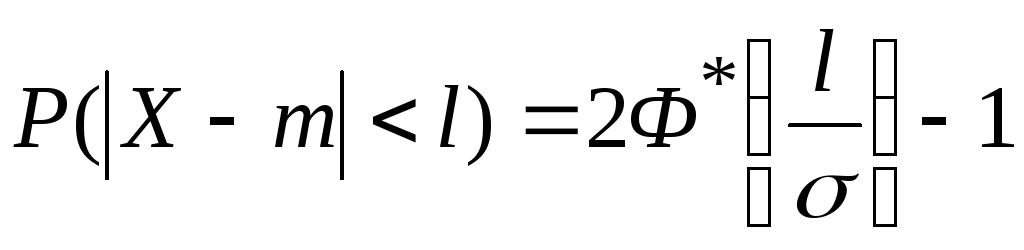4.4. Равномерное распределение.

Рассмотрим непрерывную случайную величину X, подчиненную закону равномерной плотности на участке от до(рис. 4.4.2), и напишем для нее выражение плотности распределения f(х). Плотность f(х) постоянна и равна с на отрезке (;); вне этого отрезка она равна нулю:

(4.4.1)

Определим постоянную с из условия, получим

Тогда

(4.4.2)

Выражение для функции распределения F(х) равномерно распределенной случайной величины имеет вид:

(4.4.3)

График функции F(х) приведен на рис. 4.4.1. Определим основные числовые характеристики случайной величины X, подчиненной закону равномерной плотности на участке от до.

Математическое ожидание величины Х равно:

(4.4.4)

В силу симметричности равномерного распределения медиана величины Х также равна .

Моды закон равномерной плотности не имеет. Находим дисперсию величины X:

(4.4.5)

откуда среднеквадратическое отклонение . В силу симметричности распределения его асимметрия равна нулю:

(4.4.6)

Найдем вероятность попадания случайной величины X, распределенной по закону равномерной плотности, на участок (a,b), представляющий собой часть участка ()(рис. 4.4.3).

Геометрически эта вероятность представляет собой площадь, заштрихованную на рис. 4.4.3. Очевидно, она равна:

т. е. отношению длины отрезка ко всей длине участка, на котором задано равномерное распределение.

4.5. Показательное распределение.

Непрерывна случайная величина Х имеет показательный закон распределения, если ее функция распределения имеет вид

(4.5.1)

где - параметр распределения.

Плотность распределения определится соотношением:

(4.5.2)

Плотность распределения иллюстрируются следующим графиком:

Экспоненциальное распределение

Определим числовые характеристики случайной величины распределенной по показательному закону.

	(4.5.3)
	(4.5.4)
;	(4.5.5)

4.6.Нормальный закон распределения.

Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это — наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других, состоит в том, что он является предельным, к которому приближаются другие законы распределения при весьма часто встречающихся условиях.

Можно доказать, что сумма достаточно большого числа незави­симых случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых — элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному.

Нормальный закон распределения характеризуется плотностью вероятности вида:

(4.6.1)

Кривая распределения по нормальному закону имеет симметрич­ный холмообразный вид (рис. 4.6.1). Максимальная ордината кривой, равная , соответствует точке X=т; по мере удаления от точки т плотность распределения уменьшается, и при кривая асимптотически приближается к оси абсцисс.

Выясним смысл параметров m и , входящих в выражение нормального закона; докажем, что величина т есть не что иное, как математическое ожидание, а величина — среднеквадратическое отклонение величины X. Для этого вычислим основные числовые характеристики случайной величины Х.

Применяя замену переменной, имеем:

Нетрудно убедиться, что первый из двух интервалов равен нулю; второй представляет собой известный интеграл Эйлера — Пуассона:

(4.6.2)

Следовательно,

(4.6.3)

Вычислим дисперсию величины X.

(4.6.4)

Применив снова замену переменной, имеем:

Интегрируя по частям, получим:

Первое слагаемое в фигурных скобках равно нулю (так как приубывает быстрее, чем возрастает любая степеньt), второе слагаемое равно , откуда .

Следовательно, параметр есть не что иное, как среднеквадратическое отклонение величины X.

Из соотношения (4.6.1) следует, что центром симметрии распределения является центр рассеивания т. Это ясно из того, что при изменении знака разности (x - т) на обратный выражение (4.6.1) не меняется. Если изменять центр рассеивания т кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 4.6.2).

Параметр характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна; при увеличениимаксимальная ордината уменьшается.

На рис. 4.6.3 показаны три нормальные кривые (I, II, III) при m = 0; из них кривая I соответствует

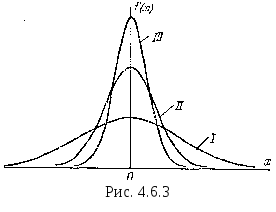
самому большому, а кривая III — самому малому значению .

Размерность параметра , естественно, совпадает с размерностью случайной величины X.

Моменты нормального распределения.

Выше мы доказали, что математическое ожидание случайной величины, подчиненной нормальному закону (4.6.1), равно т, а среднеквадратическое отклонение равно .

Выведем общие формулы для центральных моментов любого порядка.

По определению:

(4.6.5)

Делая замену переменной

получим:

(4.6.6)

проинтегрируем по частям, получим

(4.6.7)

Имея в виду, что первый член внутри скобок равен нулю, получим:

Из формулы (4.6.6) имеем следующее выражение для :

(4.6.8)

следовательно

(4.6.9)

Формула (4.6.9) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что и, можно вычислить центральные моменты всех порядков. Так как, то из формулы (4.6.9) следует, что все нечетные моменты нормального распределения равны нулю.

Для четных s из формулы (4.6.9) вытекают следующие выражения для последовательности моментов:

;;

Общая формула для момента s-го порядка при любом четном s имеет вид:

(4.6.10)

где под символам (s—1)!! понимается произведение всех нечетных чисел от 1 до s-1.

Так как для нормального закона , то асимметрия его также равна нулю:

(4.6.11)

Из выражения четвертого момента имеем:

, т. е. эксцесс нормального распределения равен нулю. Это и естественно, так как назначение эксцесса—характеризовать сравнительную крутость данного закона по сравнению с нормальным.

Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения.

Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X на участок от до. Для вычисления этой вероятности воспользуемся общей формулой

(4.6.12)

где F(х) — функция распределения случайной величины X.

Найдем функцию распределения F(х) случайной величины X распределенной по нормальному закону с параметрами т,.

(4.6.13)

Сделаем в интеграле замену переменной и приведем его к виду:

(4.6.14)

Данный интеграл не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения или(так называемыйинтеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:

	(4.6.15)

и т.д.

Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами m=0, =1.

Условимся называть функцию Ф*(х) нормальной функцией распределения. Очевидно, что

(4.6.16)

Теперь найдем вероятность попадания случайной величины Х на участок от до.

(4.6.17)

Таким образом, мы выразили вероятность попадания на интервал случайной величины X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения Ф*(х), соответствующую простейшему нормальному закону с параметрами 0,1.

Как и всякая функция распределения, функция Ф*(х) обладает свойствами:

1. Ф*()= 0.

2. Ф*()= 1.

3. Ф*(x) - неубывающая функция.

Кроме того, из симметричности нормального распределения с параметрами m=0, =1 относительно начала координат следует, что

(4.6.18)

На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания т. Рассмотрим такой участок длины 2l (рис. 4.6.4). Вычислим вероятность попадания на этот участок:

(4.6.19)

Учитывая свойство (4.6.18) функции Ф*(х) и придавая левой части формулы (4.6.19) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону, на участок, симметричный относительно центра рассеивания:

(4.6.20)

Решим следующую задачу. Отложим от центра рассеивания т последовательные отрезки длиной (рис. 4.6.5) и вычислим вероятность попадания случайной величины Х в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону. По формуле (4.6.17) находим:

Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т. д.) с точностью до 0,001 равны нулю.

Округляя вероятности попадания в отрезки до 0,01 (до 1%) получим три числа, которые легко запомнить:

0,34; 0,14; 0,01.

Сумма этих трех значений близка 0,5. Это значит, что для нор­мально распределенной случайной величины все рассеивание (с точ­ностью до долей процента) укладывается на участке т ± 3.

Это позволяет, зная среднеквадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма».
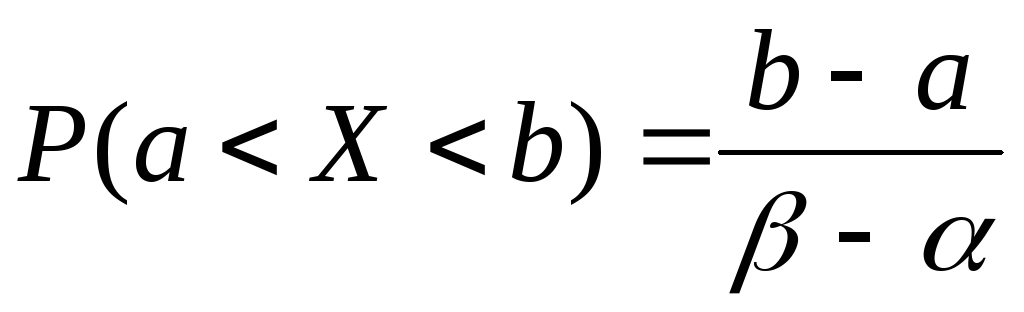