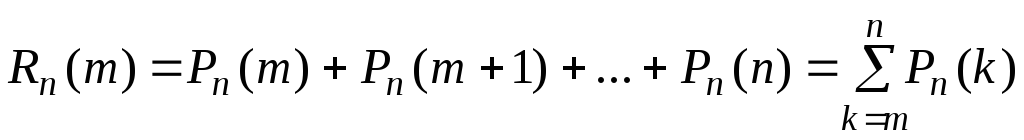- •Теория вероятностей
- •Содержание
- •Раздел 6. Законы распределения функций случайных аргументов. 90
- •1. Теоретическая часть. Введение
- •Раздел 1. Понятие события и его вероятности.
- •1.1. Предмет теории вероятности.
- •1.2. Алгебра событий. Пространство элементарных событий.
- •1.3. Классическое определение вероятности.
- •1.4. Геометрические вероятности.
- •1.5. Частота и вероятность.
- •1.6. Аксиоматическое построение теории вероятностей.
- •1.7. Условная вероятность и простейшие основные формулы.
- •1.8. Формула полной вероятности.
- •1.9 Формула Бейеса.
- •Раздел 2. Последовательные независимые испытания
- •2.1. Независимые испытания. Формулы Бернулли.
- •2.2. Обобщенная теорема о повторении опытов.
- •Раздел 3. Понятие случайной величины. Функция распределения и ее основные свойства.
- •3.1. Понятие случайной величины и функции распределения.
- •3.2. Свойства функции распределения.
- •3.3. Дискретные и непрерывные случайные величины.
- •3.4. Числовые характеристики случайных величин.
- •Раздел 4. Примеры распределений случайных величин.
- •4.1. Биномиальное распределение.
- •4.2. Теорема Пуассона
- •4.3. Закон Пуассона.
- •4.4. Равномерное распределение.
- •4.5. Показательное распределение.
- •4.6.Нормальный закон распределения.
- •Раздел 5. Системы случайных величин (случайные векторы).
- •5.1. Понятие о системе случайных величин.
- •5.2. Функция распределения системы двух случайных величин.
- •5.3. Плотность распределения системы двух случайных величин.
- •5.4. Законы распределения отдельных компонент, входящих в систему. Условные законы распределения.
- •5.5. Зависимые и независимые случайные величины.
- •5.6. Числовые характеристики системы двух случайных величин.
- •5.7. Система произвольного числа случайных величин (случайные вектора).
- •5.8. Числовые характеристики системы нескольких случайных величин.
- •Раздел 6. Законы распределения функций случайных аргументов.
- •6.1. Закон распределения функции одного случайного аргумента.
- •6.2. Закон распределения функции двух случайных величин.
- •6.3. Закон распределения суммы двух случайных величин. Композиция законов распределения.
- •6.4. Распределение произведения.
- •6.5. Распределение квадрата случайной величины.
- •6.6. Распределение частного.
- •6.7. Числовые характеристики функций случайных величин.
- •Раздел 7. Теоремы о числовых характеристиках.
- •7.1. Основные теоремы о математическом ожидании.
- •7.2. Теоремы о дисперсии случайной величины.
- •7.3. Теорема о линейной зависимости случайных величин.
- •Раздел 8. Характеристические функции.
- •8.1. Определение и простейшие свойства характеристических функций.
- •8.2. Предельные теоремы для характеристических функций.
- •Раздел 9. Предельные теоремы для случайных величин.
- •9.1. Сходимость последовательностей случайных величин.
- •9.2. Закон больших чисел.
- •9.3. Следствия закона больших чисел.
- •Раздел 10. Предельные теоремы теории вероятностей.
- •10.1. Центральная предельная теорема.
- •10.2. Теорема Ляпунова.
- •10.3. Теорема Лапласа.
- •2. Практические занятия, тесты, самостоятельная работа. Занятие 1. Непосредственный подсчет вероятности с использованием классического определения вероятности.
- •1.1. Краткая теоретическая часть.
- •1.2. Тест.
- •1.3. Решение типовых задач.
- •1.4. Задачи для самостоятельной работы.
- •Занятие 2. Геометрическое определение вероятности.
- •2.1. Краткая теоретическая часть.
- •2.2. Тест
- •2.3. Решение типовых задач
- •2.4. Задачи для самостоятельной работы
- •Занятие 3. Условная вероятность. Теорема умножения вероятностей.
- •3.1. Краткая теоретическая часть
- •3.2. Тест
- •3.3. Решение типовых задач
- •3.4. Задачи для самостоятельной работы
- •Занятие 4. Теорема сложения вероятностей.
- •4.1. Краткая теоретическая часть
- •4.2. Тест
- •4.3. Решение типовых задач
- •4.4. Задачи для самостоятельной работы
- •Занятие 5. Формула полной вероятности.
- •5.1. Краткая теоретическая часть
- •5.2. Тест.
- •5.3. Решение типовых задач
- •5.4. Задачи для самостоятельной работы
- •Занятие 6. Формула Бейеса.
- •6.1. Краткая теоретическая часть
- •6.2.Тест
- •6.3. Решение типовых задач
- •6.4. Задачи для самостоятельной работы
- •Занятие 7. Последовательные независимые испытания.
- •7.1. Краткая теоретическая часть
- •7.2. Тест
- •7.3. Решение типовых задач
- •7.4. Задачи для самостоятельной работы
- •Занятие 8. Дискретные и непрерывные случайные величины.
- •8.1. Краткая теоретическая часть а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •8.2. Тест
- •А) только к дискретным случайным величинам
- •8.3. Решение типовых задач а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Б) Функция распределения и плотность вероятности непрерывной случайной величины
- •8.4. Задачи для самостоятельной работы а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Занятие 9. Числовые характеристики дискретных случайных величин.
- •9.1. Краткая теоретическая часть
- •9.2. Тест
- •9.3. Решение типовых задач
- •9.4. Задачи для самостоятельной работы
- •Занятие 10. Дискретные и непрерывные случайные величины.
- •10.1. Краткая теоретическая часть
- •10.2. Тест
- •10.3. Решение типовых задач
- •10.4. Задачи для самостоятельной работы
- •Занятие 11. Закон Пуассона.
- •11.1. Краткая теоретическая часть
- •11.2. Тест
- •11.3. Решение типовых задач
- •11.4. Задачи для самостоятельной работы
- •Занятие 12. Закон нормального распределения.
- •12.1. Краткая теоретическая часть
- •12.2. Тест
- •12.3. Решение типовых задач
- •12.4. Задачи для самостоятельной работы
- •Литература
Занятие 7. Последовательные независимые испытания.
7.1. Краткая теоретическая часть
В настоящем разделе мы изучим основные закономерности, относящиеся к одной из важнейших схем теории вероятностей — схеме последовательных независимых испытаний. В это понятие мы вкладываем следующий смысл.
Под испытанием(опытом)
мы станем понимать осуществление
определенного комплекса условий, в
результате которого может произойти
то или иное элементарное событие
пространства U
элементарных событий. Математической
моделью последовательности п
испытаний является новое пространство
![]() элементарных событий, состоящее из
точек
элементарных событий, состоящее из
точек![]() ,
где
,
где![]() - произвольная
точка пространства U,
отвечающая
испытанию с номером i.
- произвольная
точка пространства U,
отвечающая
испытанию с номером i.
Предположим, что
для s-го
испытания пространство U
разбито на k
несовместимых случайных событий
![]() ,
т. е.
предположим, что
,
т. е.
предположим, что
|
|
|
Событие
![]() назовемi-м
исходом при s-м
испытании. Обозначим вероятность i-го
исхода при s-м
испытании
через
назовемi-м
исходом при s-м
испытании. Обозначим вероятность i-го
исхода при s-м
испытании
через
![]() .
.
Обозначим через
![]() событие,
состоящее из всех тех точек
событие,
состоящее из всех тех точек![]() пространства
пространства![]() ,
для которых
,
для которых![]() .
Если в пространствеUn
имеет место равенство
.
Если в пространствеUn
имеет место равенство
![]() при любых
при любых![]()
![]() - то испытания называютсянезависимыми.
- то испытания называютсянезависимыми.
В дальнейшем мы
ограничимся случаем, когда вероятности
событий
![]() не зависят от номера испытанияs;
обозначим в этом случае
не зависят от номера испытанияs;
обозначим в этом случае
![]() ;
в силу несовместимости и единственной
возможности исходов
;
в силу несовместимости и единственной
возможности исходов![]() очевидно, имеем
очевидно, имеем![]() .
Эта схема впервые была рассмотрена Я.
Бернулли в важнейшем частном случае
.
Эта схема впервые была рассмотрена Я.
Бернулли в важнейшем частном случае![]() ;
по этой причине указанный случай носит
названиесхемы
Бернулли. В
схеме Бернулли обычно полагают
;
по этой причине указанный случай носит
названиесхемы
Бернулли. В
схеме Бернулли обычно полагают
![]() .
.
Из определения независимых испытаний вытекает следующий результат:
Теорема. Если данные п испытаний независимы, то любые т из них также независимы.
Простейшая задача,
относящаяся к схеме независимых
испытаний, состоит в определении
вероятности
![]() того, что прип
испытаниях событие А
наступит т
раз, а остальные п—т
раз наступит противоположное событие
того, что прип
испытаниях событие А
наступит т
раз, а остальные п—т
раз наступит противоположное событие
![]() ,
обозначим это событие В.
Тогда
,
обозначим это событие В.
Тогда
|
|
(7.1) |
Здесь Аi – событие состоящее в том, что событие А произойдет в i- ом испытании. Событие В представляет собой сумму несовместных событий, тогда согласно теореме сложения вероятностей получаем
|
|
(7.2) |
Вероятность каждого
слагаемого в данной сумме по теореме
умножения для независимых событий равна
![]() .
По теореме сложения вероятностей искомая
вероятность
.
По теореме сложения вероятностей искомая
вероятность![]() равна сумме только что вычисленных
вероятностей для всех различных способовт
появлений события А
и n—т
не появлений среди п
испытаний. Число таких способов, как
известно из теории сочетаний, равно
равна сумме только что вычисленных
вероятностей для всех различных способовт
появлений события А
и n—т
не появлений среди п
испытаний. Число таких способов, как
известно из теории сочетаний, равно
 ;
следовательно, искомая вероятность
равна
;
следовательно, искомая вероятность
равна
|
|
(7.3) |
Так как все возможные
несовместимые между собой исходы п
испытаний
состоят в появлении события
![]() 0
раз, 1 раз, 2 раза, ...,n
раз, то ясно, что
0
раз, 1 раз, 2 раза, ...,n
раз, то ясно, что
|
|
(7.4) |
Легко заметить,
что вероятность
![]() равна коэффициенту при
равна коэффициенту при![]() в разложении бинома
в разложении бинома![]() по степенямx.
по степенямx.
Исследуем далее,
как ведет себя вероятность при различных
значениях m.
![]() с увеличениемm
сначала возрастает, затем достигает
максимума и при дальнейшем росте m
убывает. При
этом, если
с увеличениемm
сначала возрастает, затем достигает
максимума и при дальнейшем росте m
убывает. При
этом, если
![]() является целым числом, то максимальное
значение вероятность
является целым числом, то максимальное
значение вероятность![]() принимает для двух значенийm,
а именно
принимает для двух значенийm,
а именно
![]() и
и![]() .
Если же
.
Если же![]() не является
целым числом, то максимальное значение
вероятности
не является
целым числом, то максимальное значение
вероятности
![]() достигается при
достигается при![]() ,
равном максимальному целому числу,
большему из
,
равном максимальному целому числу,
большему из![]() и
и![]() .
Число
.
Число![]() называют наивероятнейшим значением и
обозначают через
называют наивероятнейшим значением и
обозначают через![]() .
.
Поставим теперь более общую задачу.
Рассмотрим последовательность n независимых испытаний, в каждом из которых может произойти или не произойти некоторое событие А. При этом вероятность появления события в каждом испытании различна.
Обозначим
через
![]()
![]() .Аi
– событие состоящее том что А
произойдет в i-ом
испытании
.Аi
– событие состоящее том что А
произойдет в i-ом
испытании
![]() –
событие состоящее том чтоА
не произойдет в i-ом
испытании соответственно.
–
событие состоящее том чтоА
не произойдет в i-ом
испытании соответственно.
Следует определить вероятность того что событие А произойдет m раз в серии из n испытаний.
Вероятность
того, что событие А
произойдет m
раз в серии из n
испытаний равна коэффициенту при
![]() в выражении производящей функции
в выражении производящей функции
|
|
(7.5) |
то есть
|
|
(7.6) |
|
|
(7.7) |
Обозначим
через
![]() событие состоящее в том, чтоА
появляется не менее m
раз в n
независимых испытаниях, а вероятность
событие состоящее в том, чтоА
появляется не менее m
раз в n
независимых испытаниях, а вероятность
![]() обозначим
обозначим
![]() ,
тогда
,
тогда
|
|
(7.8) |
В
тех случаях когда
![]() удобно пользоваться следующей формулой
удобно пользоваться следующей формулой
|
|
(7.9) |