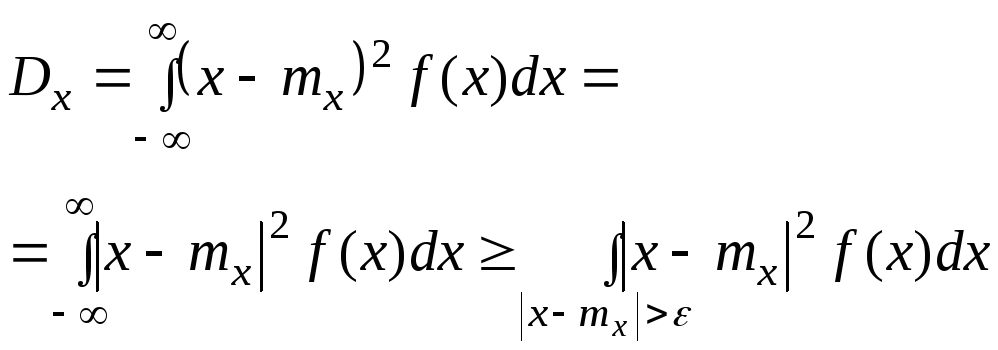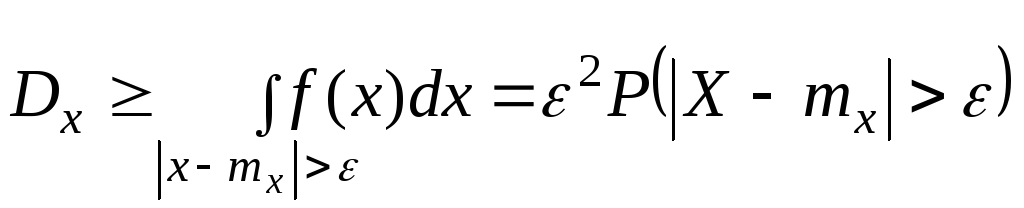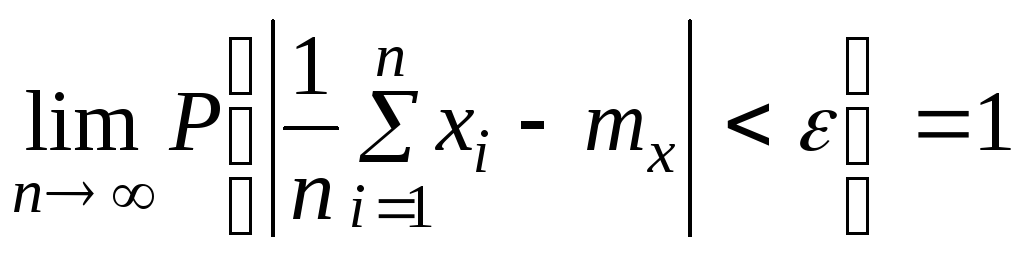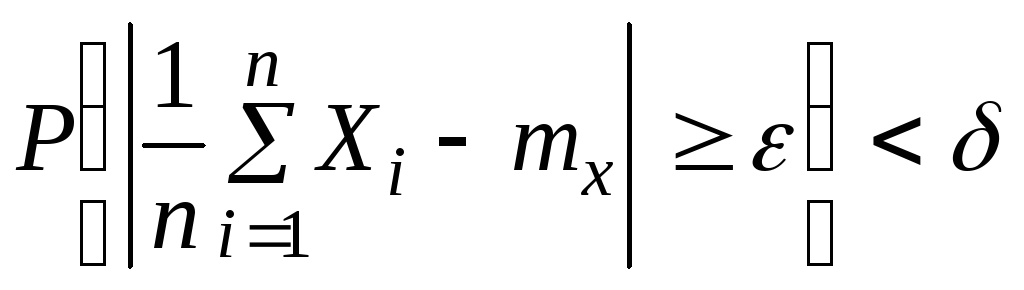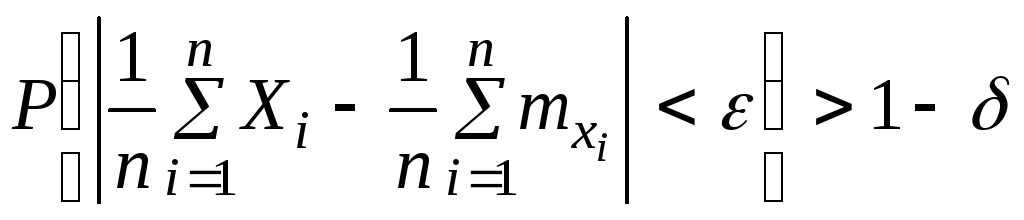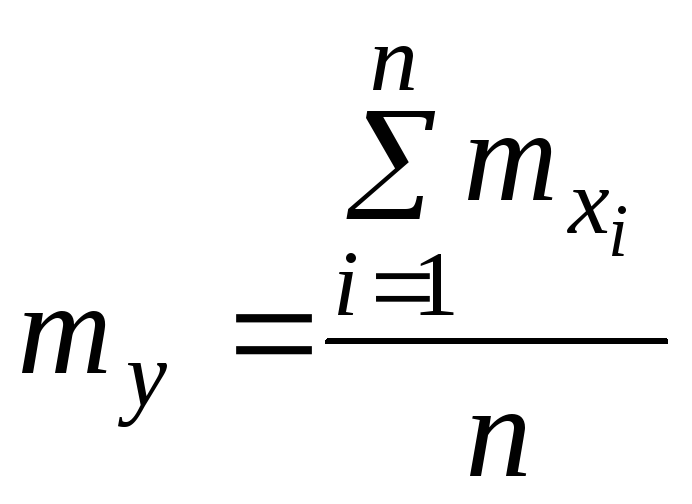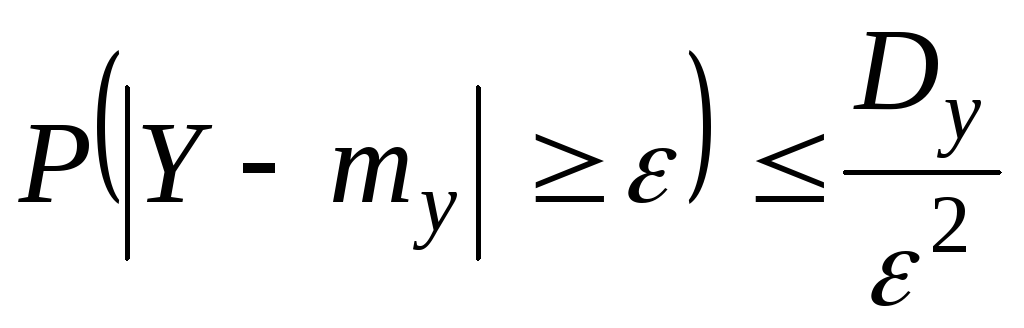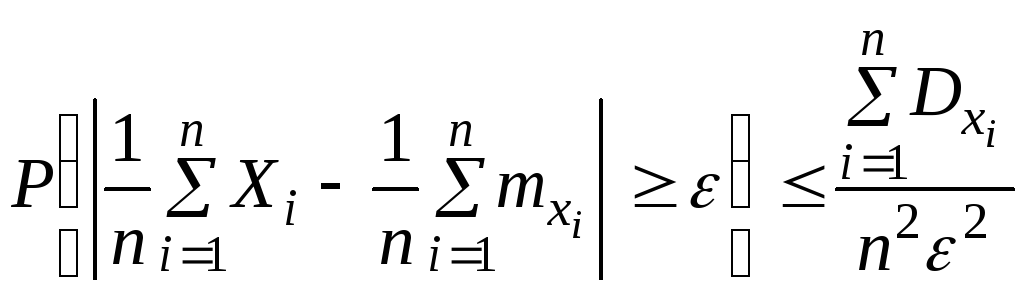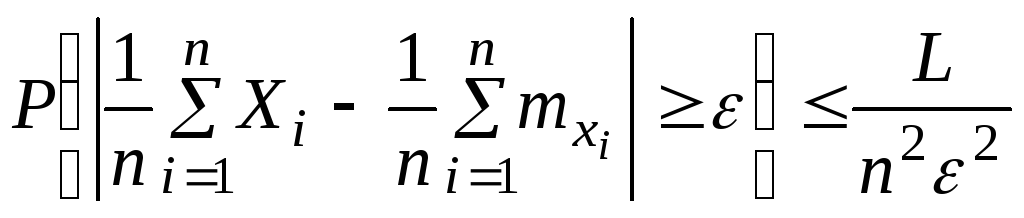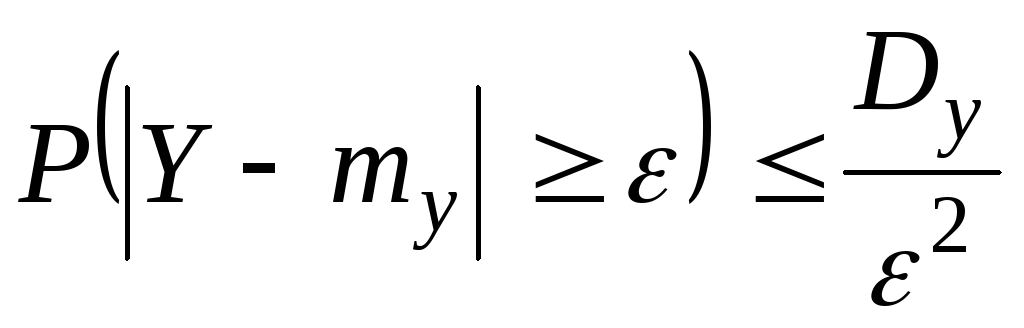- •Теория вероятностей
- •Содержание
- •Раздел 6. Законы распределения функций случайных аргументов. 90
- •1. Теоретическая часть. Введение
- •Раздел 1. Понятие события и его вероятности.
- •1.1. Предмет теории вероятности.
- •1.2. Алгебра событий. Пространство элементарных событий.
- •1.3. Классическое определение вероятности.
- •1.4. Геометрические вероятности.
- •1.5. Частота и вероятность.
- •1.6. Аксиоматическое построение теории вероятностей.
- •1.7. Условная вероятность и простейшие основные формулы.
- •1.8. Формула полной вероятности.
- •1.9 Формула Бейеса.
- •Раздел 2. Последовательные независимые испытания
- •2.1. Независимые испытания. Формулы Бернулли.
- •2.2. Обобщенная теорема о повторении опытов.
- •Раздел 3. Понятие случайной величины. Функция распределения и ее основные свойства.
- •3.1. Понятие случайной величины и функции распределения.
- •3.2. Свойства функции распределения.
- •3.3. Дискретные и непрерывные случайные величины.
- •3.4. Числовые характеристики случайных величин.
- •Раздел 4. Примеры распределений случайных величин.
- •4.1. Биномиальное распределение.
- •4.2. Теорема Пуассона
- •4.3. Закон Пуассона.
- •4.4. Равномерное распределение.
- •4.5. Показательное распределение.
- •4.6.Нормальный закон распределения.
- •Раздел 5. Системы случайных величин (случайные векторы).
- •5.1. Понятие о системе случайных величин.
- •5.2. Функция распределения системы двух случайных величин.
- •5.3. Плотность распределения системы двух случайных величин.
- •5.4. Законы распределения отдельных компонент, входящих в систему. Условные законы распределения.
- •5.5. Зависимые и независимые случайные величины.
- •5.6. Числовые характеристики системы двух случайных величин.
- •5.7. Система произвольного числа случайных величин (случайные вектора).
- •5.8. Числовые характеристики системы нескольких случайных величин.
- •Раздел 6. Законы распределения функций случайных аргументов.
- •6.1. Закон распределения функции одного случайного аргумента.
- •6.2. Закон распределения функции двух случайных величин.
- •6.3. Закон распределения суммы двух случайных величин. Композиция законов распределения.
- •6.4. Распределение произведения.
- •6.5. Распределение квадрата случайной величины.
- •6.6. Распределение частного.
- •6.7. Числовые характеристики функций случайных величин.
- •Раздел 7. Теоремы о числовых характеристиках.
- •7.1. Основные теоремы о математическом ожидании.
- •7.2. Теоремы о дисперсии случайной величины.
- •7.3. Теорема о линейной зависимости случайных величин.
- •Раздел 8. Характеристические функции.
- •8.1. Определение и простейшие свойства характеристических функций.
- •8.2. Предельные теоремы для характеристических функций.
- •Раздел 9. Предельные теоремы для случайных величин.
- •9.1. Сходимость последовательностей случайных величин.
- •9.2. Закон больших чисел.
- •9.3. Следствия закона больших чисел.
- •Раздел 10. Предельные теоремы теории вероятностей.
- •10.1. Центральная предельная теорема.
- •10.2. Теорема Ляпунова.
- •10.3. Теорема Лапласа.
- •2. Практические занятия, тесты, самостоятельная работа. Занятие 1. Непосредственный подсчет вероятности с использованием классического определения вероятности.
- •1.1. Краткая теоретическая часть.
- •1.2. Тест.
- •1.3. Решение типовых задач.
- •1.4. Задачи для самостоятельной работы.
- •Занятие 2. Геометрическое определение вероятности.
- •2.1. Краткая теоретическая часть.
- •2.2. Тест
- •2.3. Решение типовых задач
- •2.4. Задачи для самостоятельной работы
- •Занятие 3. Условная вероятность. Теорема умножения вероятностей.
- •3.1. Краткая теоретическая часть
- •3.2. Тест
- •3.3. Решение типовых задач
- •3.4. Задачи для самостоятельной работы
- •Занятие 4. Теорема сложения вероятностей.
- •4.1. Краткая теоретическая часть
- •4.2. Тест
- •4.3. Решение типовых задач
- •4.4. Задачи для самостоятельной работы
- •Занятие 5. Формула полной вероятности.
- •5.1. Краткая теоретическая часть
- •5.2. Тест.
- •5.3. Решение типовых задач
- •5.4. Задачи для самостоятельной работы
- •Занятие 6. Формула Бейеса.
- •6.1. Краткая теоретическая часть
- •6.2.Тест
- •6.3. Решение типовых задач
- •6.4. Задачи для самостоятельной работы
- •Занятие 7. Последовательные независимые испытания.
- •7.1. Краткая теоретическая часть
- •7.2. Тест
- •7.3. Решение типовых задач
- •7.4. Задачи для самостоятельной работы
- •Занятие 8. Дискретные и непрерывные случайные величины.
- •8.1. Краткая теоретическая часть а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •8.2. Тест
- •А) только к дискретным случайным величинам
- •8.3. Решение типовых задач а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Б) Функция распределения и плотность вероятности непрерывной случайной величины
- •8.4. Задачи для самостоятельной работы а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Занятие 9. Числовые характеристики дискретных случайных величин.
- •9.1. Краткая теоретическая часть
- •9.2. Тест
- •9.3. Решение типовых задач
- •9.4. Задачи для самостоятельной работы
- •Занятие 10. Дискретные и непрерывные случайные величины.
- •10.1. Краткая теоретическая часть
- •10.2. Тест
- •10.3. Решение типовых задач
- •10.4. Задачи для самостоятельной работы
- •Занятие 11. Закон Пуассона.
- •11.1. Краткая теоретическая часть
- •11.2. Тест
- •11.3. Решение типовых задач
- •11.4. Задачи для самостоятельной работы
- •Занятие 12. Закон нормального распределения.
- •12.1. Краткая теоретическая часть
- •12.2. Тест
- •12.3. Решение типовых задач
- •12.4. Задачи для самостоятельной работы
- •Литература
9.1. Сходимость последовательностей случайных величин.
Пусть
на вероятностном пространстве
![]() определены
случайные величины
определены
случайные величины
![]() со значениями
со значениями![]() .
.
Определение
1.
Последовательность
![]() сходится
по
вероятности (п.в)
к величине X,
если
сходится
по
вероятности (п.в)
к величине X,
если
|
|
(9.1.1) |
Обозначим
сходимость
![]() к
X
по вероятности символом
к
X
по вероятности символом
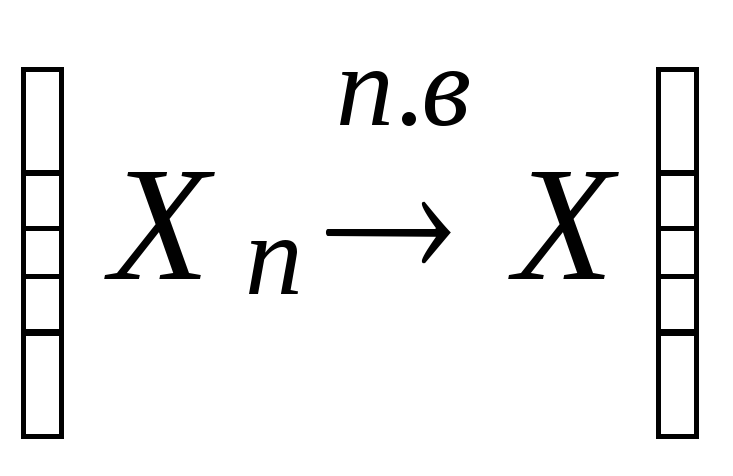 .
.
Определение
2.
Последовательность
![]() сходится
кX
почти
наверное (п.н)
(с вероятностью единица),
если
сходится
кX
почти
наверное (п.н)
(с вероятностью единица),
если
|
|
(9.1.2) |
Обозначим
эту сходимость символом
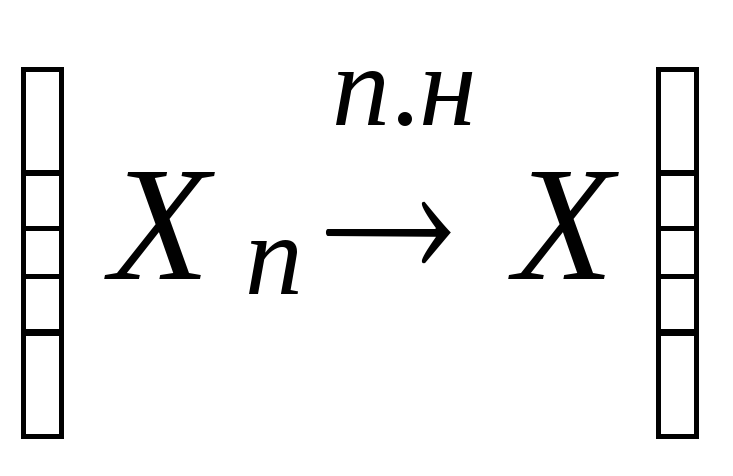 .
.
Определение
3.
Говорят, последовательность![]() сходится
кX
в среднеквадратическом (с.к.),
если
сходится
кX
в среднеквадратическом (с.к.),
если
|
|
(9.1.3) |
Обозначим
эту сходимость символом
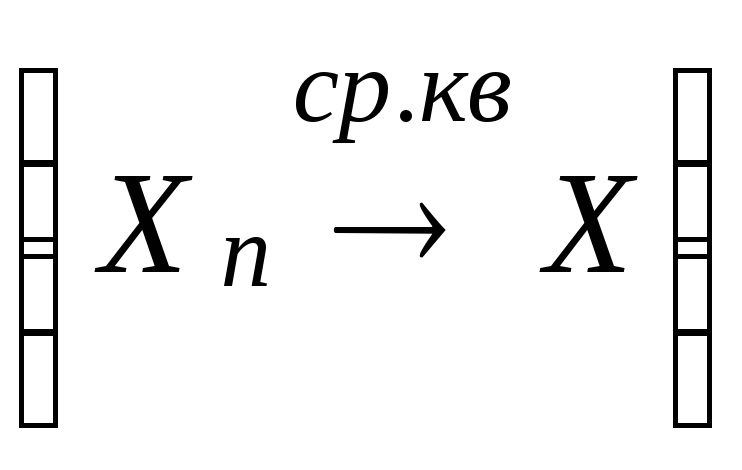 .
.
Определение
4. Последовательность
![]() сходится кX
по распределению (п.р)
с обозначением
сходится кX
по распределению (п.р)
с обозначением
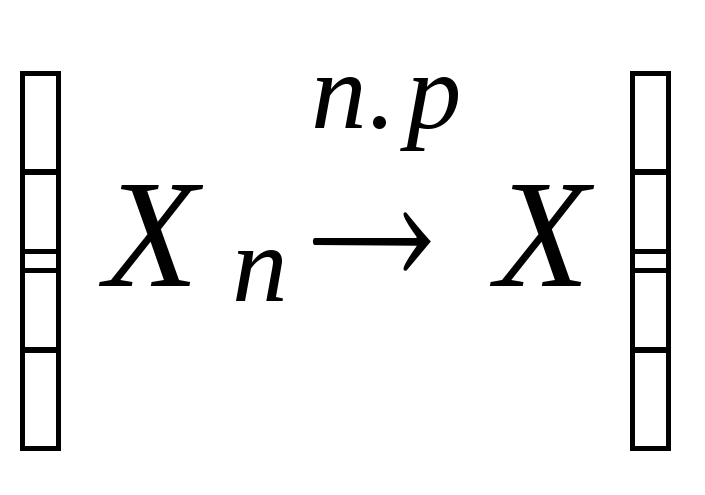 ,
если
,
если
|
|
(9.1.4) |
Здесь Fn,F- функции распределения Xn и X, причем сходимость {Fn} к F подразумевается для всех x, за исключением, может быть, точек разрыва F.
Сходимости {Xn} к X, введенные определениями 1-4, связаны между собою отношениями, показанными на рис. 9.1.1.

Рис. 9.1.1.
9.2. Закон больших чисел.
Рассмотрим ряд теорем, образующих группу теорем закона больших чисел. В качестве леммы необходимой для доказательства теорем докажем важное общее неравенство, известное под названием неравенства Чебышева.
Неравенство Чебышева.
Пусть
имеется случайная величина X
с
математическим ожиданием тх
и
дисперсией Dx.
Неравенство
Чебышева утверждает, что, каково бы ни
было положительное число
![]() ,
вероятность того, что величинаX
отклонится
от своего математического ожидания не
меньше чем на
,
вероятность того, что величинаX
отклонится
от своего математического ожидания не
меньше чем на
![]() ,
ограничена
сверху величиной —
,
ограничена
сверху величиной —![]() :
:
|
|
(9.2.1) |
Доказательство. 1. Пусть величина X дискретная, с рядом распределения:
|
|
|
|
… |
|
|
|
|
|
… |
|
Изобразим возможные значения величины X и ее математическое ожидание тх в виде точек на числовой оси Ох (рис. 9.2.1).
Зададимся
некоторым значением
![]() и вычислим вероятность того, что величинаX
отклонится
от своего математического ожидания не
меньше чем на
и вычислим вероятность того, что величинаX
отклонится
от своего математического ожидания не
меньше чем на ![]() :
:
|
|
(9.2.2) |
Для этого отложим от точки тх вправо и влево по отрезку длиной а; получим отрезок АВ. Вероятность (9.2.1) есть не что иное,

как вероятность того, что случайная точка X попадет не внутрь отрезка АВ, а вовне его:
|
|
|
Для того чтобы найти эту вероятность, нужно просуммировать вероятности всех тех значении xi, которые лежат вне отрезка АВ. Это мы запишем следующим образом:
|
|
(9.2.3) |
где
запись
![]() под знаком суммы означает, что суммирование
распространяется на все те значенияi,
для которых точки
под знаком суммы означает, что суммирование
распространяется на все те значенияi,
для которых точки
![]() лежат
вне отрезка АВ.
лежат
вне отрезка АВ.
С другой стороны, напишем выражение дисперсии величины X. По определению:
|
|
(9.2.4) |
Так как все члены суммы (9.2.4) неотрицательны, она может только уменьшиться, если мы распространим ее не на все значения xi, а только на некоторые, в частности на те, которые лежат вне отрезка АВ:
|
|
(9.2.5) |
Заменим
под знаком суммы выражение
![]() через
через
![]() .
Так как для всех членов суммы
.
Так как для всех членов суммы
![]() ,
то
от такой замены сумма тоже может только
уменьшиться; значит.
,
то
от такой замены сумма тоже может только
уменьшиться; значит.
|
|
(9.2.6) |
Но согласно формуле (9.2.3) сумма, стоящая в правой части (9.2.6). есть не что иное, как вероятность попадания случайной точки вовне отрезка АВ; следовательно,
|
|
|
откуда непосредственно вытекает доказываемое неравенство.
2. В случае, когда величина X непрерывна, доказательство проводится аналогичным образом с заменой вероятностей pi элементам вероятности, а конечных сумм — интегралами. Действительно,
|
|
|
где f(x) — плотность распределения величины X. Далее, имеем:
|
|
|
где
знак
![]() под
интегралом означает, что интегрирование
распространяется на внешнюю часть
отрезка АВ.
под
интегралом означает, что интегрирование
распространяется на внешнюю часть
отрезка АВ.
Заменяя
![]() под
знаком интеграла через
под
знаком интеграла через ![]() ,
получим:
,
получим:
|
|
|
откуда и вытекает неравенство Чебышева для непрерывных величия.
Теорема Чебышева.
Пусть
![]() последовательность независимых случайных
величин, имеющих одинаковые
последовательность независимых случайных
величин, имеющих одинаковые![]() и
и![]() .
Тогда при
.
Тогда при![]() их среднее арифметическое сходится по
вероятности к их математическому
ожиданию, то есть
их среднее арифметическое сходится по
вероятности к их математическому
ожиданию, то есть
|
|
|
Доказательство. Выше было показано, что величина
|
|
|
имеет числовые характеристики
|
|
|
Применим к случайной величине Y неравенство Чебышева:
|
|
|
Как
бы мало ни было число
![]() ,
можно взятьп
таким
большим, чтобы выполнялось неравенство
,
можно взятьп
таким
большим, чтобы выполнялось неравенство
|
|
|
где
![]() — сколь угодно малое число. Тогда
— сколь угодно малое число. Тогда
|
|
|
откуда, переходя к противоположному событию, имеем:
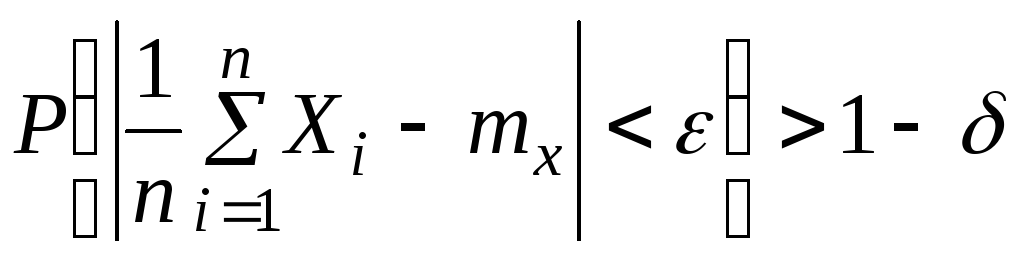 ,
что эквивалентно
,
что эквивалентно 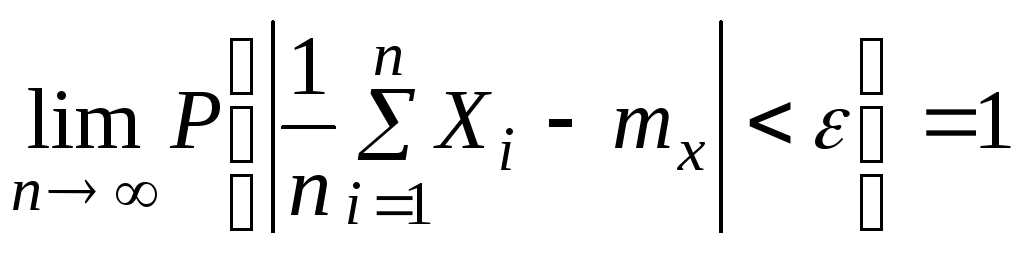
что и требовалось доказать.
Обобщенная теорема Чебышева.
Теорема
Чебышева легко может быть обобщена на
более сложный случай. Обобщенная
теорема Чебышева формулируется следующим
образом.
Если
![]() независимые
случайные величины с математическими
ожиданиями
независимые
случайные величины с математическими
ожиданиями
![]() и
дисперсиями
и
дисперсиями
![]() и
если все дисперсии ограничены сверху
одним и тем же числом L:
и
если все дисперсии ограничены сверху
одним и тем же числом L:
|
|
|
то
при возрастании п среднее арифметическое
наблюденных значений величин
![]() сходится
по вероятности к среднему арифметическому
их математических ожиданий. Запишем
эту теорему в виде формулы. Пусть
сходится
по вероятности к среднему арифметическому
их математических ожиданий. Запишем
эту теорему в виде формулы. Пусть
![]() — сколь угодно малые положительные
числа. Тогда при достаточно большомn
— сколь угодно малые положительные
числа. Тогда при достаточно большомn
|
|
|
Доказательство. Рассмотрим величину
|
|
|
Ее математическое ожидание равно:
|
|
|
а дисперсия
|
|
|
Применим к величине Y неравенство Чебышева:
|
|
|
или
|
|
(9.2.7) |
Заменим
в правой части неравенства (9.2.7) каждую
из величин
![]() большей
величиной L.
Тогда
неравенство только усилится:
большей
величиной L.
Тогда
неравенство только усилится:
|
|
|
Как
бы мало ни было
![]() ,
можно выбратьп
настолько
большим, чтобы выполнялось неравенство
,
можно выбратьп
настолько
большим, чтобы выполнялось неравенство
![]() ,тогда
,тогда
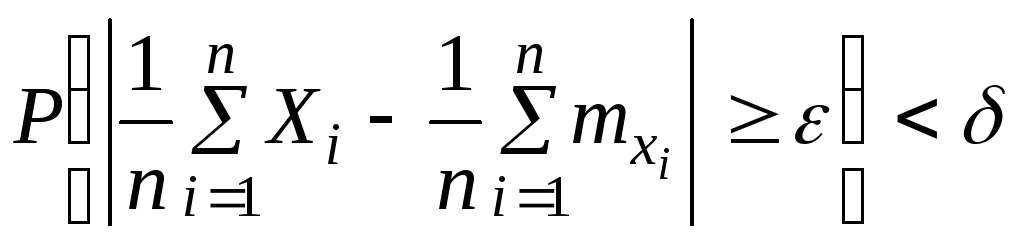 откуда,
переходя к противоположному событию,
получим доказываемое неравенство.
откуда,
переходя к противоположному событию,
получим доказываемое неравенство.
Теорема Маркова.
Закон больших чисел может быть распространен и на зависимые случайные величины. Обобщение закона больших чисел на случай зависимых случайных величин принадлежит А. А. Маркову.
Теорема.
Если
имеются зависимые случайные величины
![]() и если при
и если при
![]()
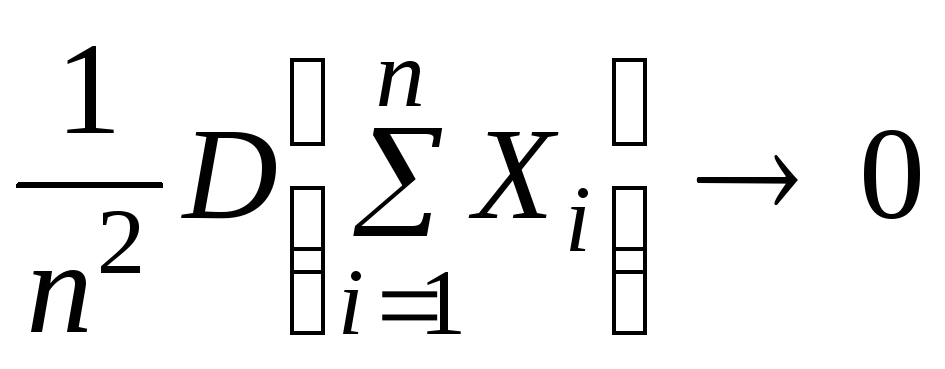 ,
то среднее арифметическое случайных
величин
,
то среднее арифметическое случайных
величин
![]() сходится по вероятности к среднему
арифметическому их математических
ожиданий.
сходится по вероятности к среднему
арифметическому их математических
ожиданий.
Доказательство. Рассмотрим величину
![]() .
Очевидно,
.
Очевидно,
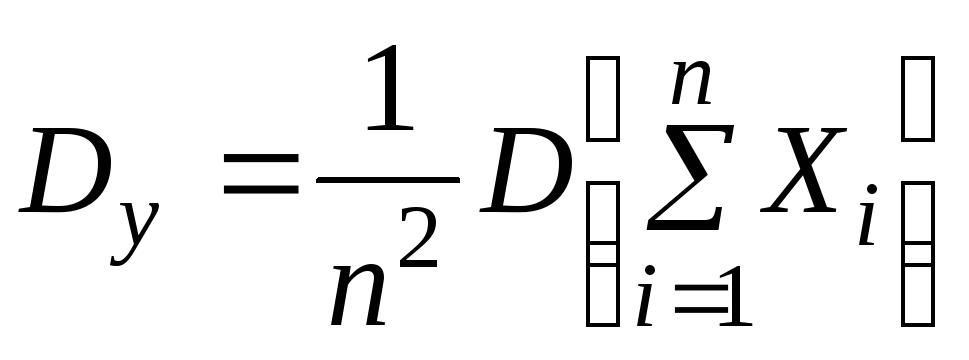 .
.
Применим к величине Y неравенство Чебышева:
|
|
|
Так
как по условию теоремы при
![]()
![]() ,
то при достаточно большомп
,
то при достаточно большомп
|
|
|
или, переходя к противоположному событию,
|
|
|
что и требовалось доказать.