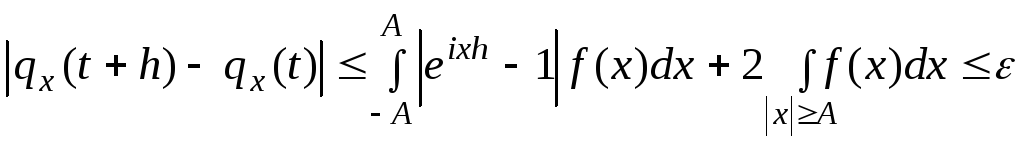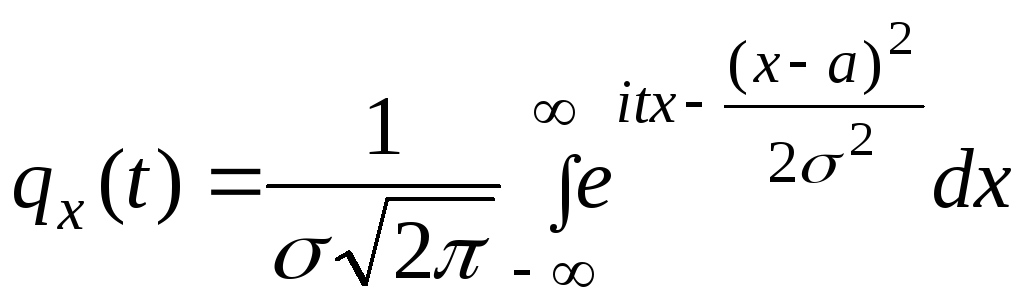- •Теория вероятностей
- •Содержание
- •Раздел 6. Законы распределения функций случайных аргументов. 90
- •1. Теоретическая часть. Введение
- •Раздел 1. Понятие события и его вероятности.
- •1.1. Предмет теории вероятности.
- •1.2. Алгебра событий. Пространство элементарных событий.
- •1.3. Классическое определение вероятности.
- •1.4. Геометрические вероятности.
- •1.5. Частота и вероятность.
- •1.6. Аксиоматическое построение теории вероятностей.
- •1.7. Условная вероятность и простейшие основные формулы.
- •1.8. Формула полной вероятности.
- •1.9 Формула Бейеса.
- •Раздел 2. Последовательные независимые испытания
- •2.1. Независимые испытания. Формулы Бернулли.
- •2.2. Обобщенная теорема о повторении опытов.
- •Раздел 3. Понятие случайной величины. Функция распределения и ее основные свойства.
- •3.1. Понятие случайной величины и функции распределения.
- •3.2. Свойства функции распределения.
- •3.3. Дискретные и непрерывные случайные величины.
- •3.4. Числовые характеристики случайных величин.
- •Раздел 4. Примеры распределений случайных величин.
- •4.1. Биномиальное распределение.
- •4.2. Теорема Пуассона
- •4.3. Закон Пуассона.
- •4.4. Равномерное распределение.
- •4.5. Показательное распределение.
- •4.6.Нормальный закон распределения.
- •Раздел 5. Системы случайных величин (случайные векторы).
- •5.1. Понятие о системе случайных величин.
- •5.2. Функция распределения системы двух случайных величин.
- •5.3. Плотность распределения системы двух случайных величин.
- •5.4. Законы распределения отдельных компонент, входящих в систему. Условные законы распределения.
- •5.5. Зависимые и независимые случайные величины.
- •5.6. Числовые характеристики системы двух случайных величин.
- •5.7. Система произвольного числа случайных величин (случайные вектора).
- •5.8. Числовые характеристики системы нескольких случайных величин.
- •Раздел 6. Законы распределения функций случайных аргументов.
- •6.1. Закон распределения функции одного случайного аргумента.
- •6.2. Закон распределения функции двух случайных величин.
- •6.3. Закон распределения суммы двух случайных величин. Композиция законов распределения.
- •6.4. Распределение произведения.
- •6.5. Распределение квадрата случайной величины.
- •6.6. Распределение частного.
- •6.7. Числовые характеристики функций случайных величин.
- •Раздел 7. Теоремы о числовых характеристиках.
- •7.1. Основные теоремы о математическом ожидании.
- •7.2. Теоремы о дисперсии случайной величины.
- •7.3. Теорема о линейной зависимости случайных величин.
- •Раздел 8. Характеристические функции.
- •8.1. Определение и простейшие свойства характеристических функций.
- •8.2. Предельные теоремы для характеристических функций.
- •Раздел 9. Предельные теоремы для случайных величин.
- •9.1. Сходимость последовательностей случайных величин.
- •9.2. Закон больших чисел.
- •9.3. Следствия закона больших чисел.
- •Раздел 10. Предельные теоремы теории вероятностей.
- •10.1. Центральная предельная теорема.
- •10.2. Теорема Ляпунова.
- •10.3. Теорема Лапласа.
- •2. Практические занятия, тесты, самостоятельная работа. Занятие 1. Непосредственный подсчет вероятности с использованием классического определения вероятности.
- •1.1. Краткая теоретическая часть.
- •1.2. Тест.
- •1.3. Решение типовых задач.
- •1.4. Задачи для самостоятельной работы.
- •Занятие 2. Геометрическое определение вероятности.
- •2.1. Краткая теоретическая часть.
- •2.2. Тест
- •2.3. Решение типовых задач
- •2.4. Задачи для самостоятельной работы
- •Занятие 3. Условная вероятность. Теорема умножения вероятностей.
- •3.1. Краткая теоретическая часть
- •3.2. Тест
- •3.3. Решение типовых задач
- •3.4. Задачи для самостоятельной работы
- •Занятие 4. Теорема сложения вероятностей.
- •4.1. Краткая теоретическая часть
- •4.2. Тест
- •4.3. Решение типовых задач
- •4.4. Задачи для самостоятельной работы
- •Занятие 5. Формула полной вероятности.
- •5.1. Краткая теоретическая часть
- •5.2. Тест.
- •5.3. Решение типовых задач
- •5.4. Задачи для самостоятельной работы
- •Занятие 6. Формула Бейеса.
- •6.1. Краткая теоретическая часть
- •6.2.Тест
- •6.3. Решение типовых задач
- •6.4. Задачи для самостоятельной работы
- •Занятие 7. Последовательные независимые испытания.
- •7.1. Краткая теоретическая часть
- •7.2. Тест
- •7.3. Решение типовых задач
- •7.4. Задачи для самостоятельной работы
- •Занятие 8. Дискретные и непрерывные случайные величины.
- •8.1. Краткая теоретическая часть а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •8.2. Тест
- •А) только к дискретным случайным величинам
- •8.3. Решение типовых задач а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Б) Функция распределения и плотность вероятности непрерывной случайной величины
- •8.4. Задачи для самостоятельной работы а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Занятие 9. Числовые характеристики дискретных случайных величин.
- •9.1. Краткая теоретическая часть
- •9.2. Тест
- •9.3. Решение типовых задач
- •9.4. Задачи для самостоятельной работы
- •Занятие 10. Дискретные и непрерывные случайные величины.
- •10.1. Краткая теоретическая часть
- •10.2. Тест
- •10.3. Решение типовых задач
- •10.4. Задачи для самостоятельной работы
- •Занятие 11. Закон Пуассона.
- •11.1. Краткая теоретическая часть
- •11.2. Тест
- •11.3. Решение типовых задач
- •11.4. Задачи для самостоятельной работы
- •Занятие 12. Закон нормального распределения.
- •12.1. Краткая теоретическая часть
- •12.2. Тест
- •12.3. Решение типовых задач
- •12.4. Задачи для самостоятельной работы
- •Литература
7.3. Теорема о линейной зависимости случайных величин.
Теорема.
Для линейной
независимости двух случайных величин
X
и Y
необходимо и достаточно, что бы
![]() .
.
Необходимость.
Пусть
![]() ,
тогда
,
тогда![]() .
Определим
.
Определим
|
|
(7.3.1) |
откуда
|
|
(7.3.2) |
Подсчитаем
коэффициент корреляции
![]() ,
получим
,
получим
|
|
(7.3.3) |
Достаточность.
Пусть
![]() .
Для определенности положим
.
Для определенности положим![]()
Введем в рассмотрение
случайную величину
 ;
; ;
; определим дисперсию случайной величиныZ
определим дисперсию случайной величиныZ
|
|
|
|
|
|
что и требовалось доказать.
Раздел 8. Характеристические функции.
Простое решение весьма многих задач теории вероятностей, особенно тех из них, которые связаны с суммированием независимых случайных величин, удается получить с помощью характеристических функций, теория которых развита в анализе и известна как преобразования Фурье.
8.1. Определение и простейшие свойства характеристических функций.
Определение
1. Характеристической
функцией
![]() случайной
величины X
называется математическое ожидание
случайной величины
случайной
величины X
называется математическое ожидание
случайной величины
![]() ,
то есть
,
то есть
|
|
(8.1.1) |
если X – дискретная случайная величина и известен ряд ее распределения, то
|
|
(8.1.2) |
если X – непрерывная случайная величина с известной плотностью распределения f(x), то
|
|
(8.1.3) |
Следует заметить, что ряд (8.1.2) и интеграл (8.1.3) сходится абсолютно. Рассмотрим сходимость на примере интеграла (8.1.3)
|
|
|
Теорема 1. Характеристическая функция равномерно непрерывна на всей прямой и удовлетворяет следующим соотношениям:
|
|
(8.1.4) |
Доказательство.
Соотношения (8.1.4) немедленно вытекают
из определения характеристической
функции. Действительно, подставляя в
(8.1.3)
![]() получим
получим

|
|
|
Откуда
![]() .
.
Нам остается доказать равномерную непрерывность функции q(x). С этой целью рассмотрим разность
|
|
(8.1.5) |
и оценим ее по модулю. Имеем:
|
|
|
Пусть
![]() произвольно; выберем столь большоеА,
чтобы
произвольно; выберем столь большоеА,
чтобы
|
|
(8.1.6) |
и
подберем столь малое h,
чтобы
для
![]() выполнилось условие
выполнилось условие
|
|
(8.1.7) |
Тогда, учитывая (8.1.6) и (8.1.7) получаем
|
|
(8.1.8) |
Это неравенство доказывает теорему.
Теорема
2. Если
![]() ,
где a
и b
—
постоянные,
то
,
где a
и b
—
постоянные,
то
|
|
(8.1.9) |
где
![]() и
и
![]() есть
характеристические функции величин Y
и
X.
есть
характеристические функции величин Y
и
X.
Доказательство. Действительно,
|
|
|
Теорема 3. Характеристическая функция суммы двух независимых случайных величин равна произведению их характеристических функций.
Доказательство.
Пусть X
и
Y
—
независимые случайные величины и
![]() .
Так как X
и
Y
независимы, то случайные величины
.
Так как X
и
Y
независимы, то случайные величины
![]() и
и![]() .Отсюда
вытекает, что
.Отсюда
вытекает, что
![]() .
.
Это доказывает теорему.
Следствие. Если
|
|
|
причем каждое слагаемое независимо от суммы предыдущих, то характеристическая функция величины X равна произведению характеристических функций слагаемых.
Применение характеристических функций в значительной степени опирается на свойство, сформулированное в теореме 3. Сложение независимых случайных величин приводит к весьма сложной операции — композиции функций распределения слагаемых. Для характеристических функций эта сложная операция заменяется весьма простой — простым умножением характеристических функций.
Теорема
4(единственности). Распределения F(x),f(x)
однозначно
определяются своей характеристической
функцией
![]() .
.
Обратное соответствие устанавливается, в частности, следующей формулой:
|
|
(8.1.10) |
Теорема 5(непрерывности).
а) Если
последовательность функций распределения
![]() сходится
к функции распределения F
в
точках ее непрерывности, то
последовательность
сходится
к функции распределения F
в
точках ее непрерывности, то
последовательность
![]() соответствующих характеристических
функций сходится к характеристической
функции
соответствующих характеристических
функций сходится к характеристической
функции![]() распределения F.
распределения F.
б) Если
последовательность характеристических
функций
![]() сходится всюду наR1
к некоторой
функции
сходится всюду наR1
к некоторой
функции
![]() ,
непрерывной в точкеt=0,
то
,
непрерывной в точкеt=0,
то
![]() есть характеристическая функция
распределенияF,
при
этом в точках непрерывности F
функция
распределения F
является
пределом последовательности распределений
есть характеристическая функция
распределенияF,
при
этом в точках непрерывности F
функция
распределения F
является
пределом последовательности распределений
![]() ,
соответствующей
,
соответствующей
![]() .
.
Теорема
6. Если
случайная величина X
имеет
абсолютный момент п-го порядка, то
характеристическая функция величины
X
дифференцируема п раз и при
![]()
|
|
(8.1.11) |
Доказательство.
Действительно, k
- кратное (![]() )формальное
дифференцирование характеристической
функции приводит к равенству
)формальное
дифференцирование характеристической
функции приводит к равенству
|
|
(8.1.12) |
Но
|
|
|
и, следовательно, в силу предположения теоремы ограничен. Отсюда следует существование интеграла (8.1.12) и законность дифференцирования. Положив в (8.1.12) t=0, получим:
|
|
|
Математическое
ожидание и дисперсия весьма просто
выражаются при помощи производных от
логарифма характеристической функции.
В самом деле, положим
![]() .
Тогда
.
Тогда
|
|
|
Приняв во внимание, что qx(0)=1 и равенство (8.1.11), находим:
|
|
|
|
|
|
Отсюда
|
|
(8.1.13) |
Производная
k-го
порядка логарифма характеристической
функции в точке 0, умноженная на
![]() ,
называется семиинвариантом
k-го
порядка случайной величины.
,
называется семиинвариантом
k-го
порядка случайной величины.
Как это непосредственно следует из теоремы 3, при сложении независимых случайных величин их семиинварианты складываются.
Мы только что видели, что первыми двумя семиинвариантами являются математическое ожидание и дисперсия, т. е. момент первого порядка и некоторая рациональная функция моментов первого и второго порядков. Путем вычислений легко убедиться, что семиинвариант любого порядка k есть (целая) рациональная функция первых k моментов. Для примера приведем явные выражения семиинвариантов третьего и четвертого порядков:
|
|
|
|
|
|
Рассмотрим теперь несколько примеров характеристических функций.
Пример
1. Случайная величина X
распределена по нормальному закону с
математическим ожиданием а
и
дисперсией
![]() .
Характеристическая функция величины
равна
.
Характеристическая функция величины
равна
|
|
|
Подстановкой
|
|
|
![]() приводится к виду
приводится к виду
|
|
|
Известно, что при любом вещественном a
|
|
|
следовательно.
|
|
|
В частном случае,
когда
![]() ,
то естьa=0,
а
,
то естьa=0,
а
![]() =1,
то характеристическая функция имеет
вид
=1,
то характеристическая функция имеет
вид
![]() .
.
Пример 2. Найти характеристическую функцию случайной величины X, распределенной по закону Пуассона.
Согласно предположению, случайная величина X принимает только целочисленные значения, причем
|
|
|
где
![]() — постоянная. Характеристическая
функция величиныX
равна
— постоянная. Характеристическая
функция величиныX
равна
|
|
|
отсюда находим:
|
|
|