§ 2. Схемы дедуктивных умозаключений

Умозаключение дает истинное заключение, если исходные посылки истинны и соблюдены правила вывода, или, как их еще называют, схемы дедуктивных умозаключений.

Рассмотрим наиболее часто использующиеся правила.

1. Правило заключения:.

В данном правиле А(х)В(х) – общая посылка. Это может быть теорема, определение и, вообще предложение видаА(х)В(х). Вторая посылкаА(а) – частная посылка, а предложениеВ(а) – заключение.

Пример: Все числа, оканчивающиеся нулем, делятся на 10. Число 50 оканчивается нулем. Следовательно, число 50 делится на 10.

В основе этого правила лежит тождественно истинная формула ((АВ)А)В).

Докажем тождественную истинность этой формулы при помощи таблицы истинности.

А	В	А В	А В  А	(А В  А) В
И	И	И	И	И
И	Л	Л	Л	И
Л	И	И	Л	И
Л	Л	И	Л	И

1. Правило отрицания:.

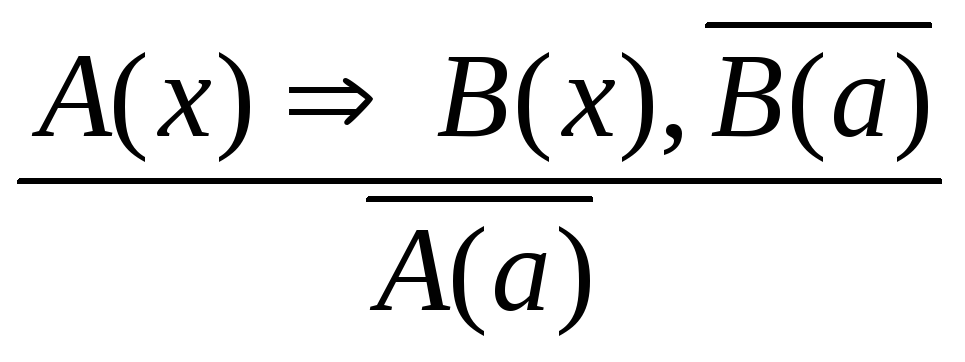Пример. Если число делится на 6, то оно делится на 3. Число 28 не делится на 3. следовательно, число 28 не делится на 6.

В основе этого правила лежит тождественно истинная формула ((АВ))).

А	В	А В		А В		(А В)
И	И	И	Л	Л	Л	И
И	Л	Л	И	Л	Л	И
Л	И	И	Л	Л	И	И
Л	Л	И	И	И	И	И

3. Правило силлогизма:.

Пример. Все квадраты – ромбы. Все ромбы – параллелограммы. Следовательно, все квадраты – параллелограммы.

В основе правила лежит тождественно истинная формула (АВ)ВС)(АС).

А	В	С	АВ	В С	(АВ)(В С)	АС	(АВ)ВС)(АС)
И	И	И	И	И	И	И	И
И	И	Л	И	Л	Л	Л	И
И	Л	И	Л	И	Л	И	И
Л	И	И	И	И	И	И	И
Л	Л	И	И	И	И	И	И
Л	И	Л	И	Л	Л	И	И
И	Л	Л	Л	И	Л	Л	И
Л	Л	Л	И	И	И	И	И

4. Правило контрапозиции:.

Пример. Если углы смежные, то их сумма равна 180^о. Следовательно, если сумма углов не равна 180^о, то углы не смежные.

В основе этого правила лежит тождественно истинная формула (АВ)().

А	В			А В		(АВ)()
И	И	Л	Л	И	И	И
И	Л	Л	И	Л	Л	И
Л	И	И	Л	И	И	И
Л	Л	И	И	И	И	И

§ 3. Проверка правильности умозаключений

В логике существуют различные способы проверки правильности умозаключений.

Один из них – с использованием кругов Эйлера. Данное умозаключение вначале записывают на теоретико-множественном языке и изображают посылки на кругах Эйлера.

Словесная формулировка	Запись на теоретико-множественном языке	Изображение на кругах Эйлера
Всякое АестьВ	А В	А В
Некоторые АестьВ	АВ	А В
Некоторые Ане естьВ	АВ	А В
Ни одно Ане естьВ	АВ=	А В
а естьА	аА	А
а не естьА	аА	А  а

Изображая посылки на кругах Эйлера, считают их истинными. После этого выясняют, всегдали при таких посылках истинно заключение. Если всегда – умозаключение правильное; если же возможен рисунок, из которого видно, что заключение может быть ложным, то умозаключение неправильное.

П

В

ример1. Все числа, делящиеся на 10, делятся на 5. число 140 делится на 10. Следовательно, число 140 делится на 5.

З

А

апишем данное умозаключение на теоретико-множественном языке, для чего обозначим черезАмножество чисел, делящихся на 10, черезВмножество чисел, делящихся на 5. Тогда умозаключение можно записать в виде:. Изобразив посылки на кругах Эйлера, видим, что в этом случаеаВ, т.е. умозаключение построено правильно.

Пример2. Все числа, делящиеся на 10, делятся на 5. Число 47 не делится на 10. Следовательно, число 47 не делится на 5. На теоретико-множественном языке умозаключение

п

В

А

В

А

 а

римет вид:. Изобразим посылки на кругах Эйлера и посмотрим, обязательно лиаВ. По первому рисунку видно, что возможен случай, когдааВ. Следовательно, заключение логически не следует из посылок, т.е. умозаключение построено неправильно.

Математические софизмы

В математике давно заметили, что использование схем, не гарантирующих истинность заключения, приводят к неверному выводу, лонному заключению. Математики стали умышленно придумывать неправильные рассуждения, имеющие видимость правильных.

Софизмомназывается умышленно ложное умозаключение, которое имеет видимость правильного. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах выполняются «запрещенные» действия или не учитываются условия применения теорем, формул и правил. Иногда рассуждения ведутся с использованием ошибочного чертежа или опираются на приводящие к ошибочным заключениям «очевидности».

В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости математических рассуждений и содействовали более глубокому уяснению понятий и методов математики.

Разбор софизмов прежде всего развивает логическое мышление, т.е. прививает навыки правильного мышления. Обнаружить ошибку в софизме – это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях.

Пример 1. Докажем, что 5 = 1. Будем рассуждать так: из чисел 5 и 1 по отдельности вычтем одно и тоже число 3. Получим числа 2 и –2. при возведении в квадрат этих чисел получаются равные числа 4 и 4. Значит, должны быть и исходные числа 5 и 1. Необходимо указать, где допущена ошибка. Ошибка в следующем: из равенства квадратов двух чисел не следует, что сами эти числа равны.

Пример 2. Докажем, что спичка вдвое длиннее телеграфного столба. Пустьа– дли на спички (дм) иb– длина столба (дм). Разность междуb и аобозначим черезс. Имеем:b – а=с,b = а+с. Перемножая эти два равенства по частям, находим:b²–ab = ca+ c². Вычтем из обеих частейbc. Получим:b²–ab – bc = ca+ c²–bc, илиb(b–a – c) = – c(b–a – c), откудаb = –с, ноb – а=с, поэтомуb = а– b, илиа= 2b, т.е. спичка вдвое длиннее телеграфного столба. Ошибка состоит в том, что нельзя делить наb–a – c, т.к.b–a – c= 0.